(Des)
求对于正整数(nleq 1e5),{(1,2,3,...,n)}的满足约束条件:"若(x)在该子集中,则(2x)和(3x)不在该子集中."的子集个数.
(Sol)
是一道很妙的构造+状压(dp)题吖.
我最开始想这题的时候画了一个如下的图.对于每一个点,左儿子是它的两倍,右儿子是它的三倍.
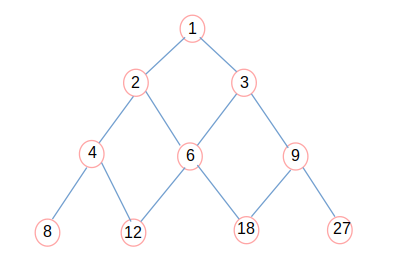
约束条件是:连了边的两个点是不可以同时选的,也就是只能隔一个选一个,但是这样显然不好做.于是考虑能不能再转化一下.仔细观察这个图会发现它特别像一棵树,但又不是,因为一个点有两个父亲,这是因为一个数可能是一个数的两倍同时又是另外一个数的三倍.再观察一下会发现这个图似乎是由许多小菱形组成的,于是把菱形拉成正方形会发现得到了一个倒三角.如下:

显然我们可以把这个倒三角填满得到一个网格图.对于每一个点,它的下面是它的两倍,右边是它的三倍.这样一来,约束条件就变成了选了一个数,就不能选与它相邻的数(上,下,左,右).转化之后就成为了一般的状压$dp $解决的问题.但是,注意到这个表格并不能涵盖所有的数,我们需要对没有被涵盖的数再建一个如上的网格图,最后乘法原理统计下答案就好了.
温馨提醒
大数组别用(memset),你很有可能会向我一样(T)掉.
(Code)
Code
```cpp
#include
#define il inline
#define Ri register int
#define go(i,a,b) for(Ri i=a;i<=b;++i)
#define yes(i,a,b) for(Ri i=a;i>=b;--i)
#define e(i,u) for(Ri i=b[u];i;i=a[i].nt)
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
#define db double
#define inf 2147483647
using namespace std;
il int read()
{
Ri x=0,y=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')y=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
return x*y;
}
const int N=100010,mod=1e9+1;
int n,h[30],a[30][30],f[30][100000];ll as=1;//h[0]:一共有多少行 h[i]:第i行有多少数
vectorb[30];
bool vis[N];
il void build(Ri x)
{
mem(h,0);
while(x<=n)
{
Ri y=x;++h[0];
while(y<=n)vis[y]=1,a[h[0]][++h[h[0]]]=y,y*=2;
x*=3;
}
}
il bool ck(Ri x,Ri ct)
{
go(i,0,ct)if(x&(1<mod)f[i][j]-=mod;
}
}
ll ret=0;
go(j,0,(int)b[h[0]].size()-1)
{
ret=ret+f[h[0]][j];
if(ret>mod)ret-=mod;
}
return ret;
}
int main()
{
n=read();
go(i,1,n)
{
if(vis[i])continue;
build(i);as=as*sol();if(as>mod)as%=mod;
}
printf("%lld
",as);
return 0;
}
<details>

