题意:求n个数中第k小的数
题解:
//由快速排序算法演变而来的快速选择算法
#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N];
//k是整个区间中的第k小的数。
void quick(int l,int r,int k)
{//快速选择算法保证每次递归时都递归到答案所在的区间.
int i=l-1,j=r+1,x=a[l+r>>1];
if(l>=r)return a[r];
while(i<j)
{
while(a[++i]<x);
while(a[--j]>x);
if(i<j)swap(a[i],a[j]);
}
cout<<"i: "<<i<<"j: "<<j<<"x: "<<x<<endl;
quick(l,j);
quick(j+1,r);
}
/*
5
2 3 4 5 1
i: 3j: 2x: 4
i: 2j: 1x: 3
i: 1j: 0x: 2
i: 4j: 3x: 5
1 2 3 4 5
通过一组测试数据发现i+1==x,i-1=j; j是x在数组中的下标
得到数组中比<=x的数有j+1个
扩展问题:求第k大的数
基础问题:求第k小的数
每次统计<=x的数的个数及j+1,如果j+1<=cnt左边去递归
否则右边去递归
*/
int main()
{
int n,k;cin>>n>>k;
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
quick(0,n-1,k);
for(int i=0;i<n;i++)
printf("%d ",a[i]);
return 0;
}
代码:
#include<iostream>
using namespace std;
const int N=1e6+10;
int a[N];
int quick(int l,int r,int k)
{
int i=l-1,j=r+1,x=a[l+r>>1];
if(l>=r)return a[l];
while(i<j)
{
while(a[++i]<x);
while(a[--j]>x);
if(i<j)swap(a[i],a[j]);
}
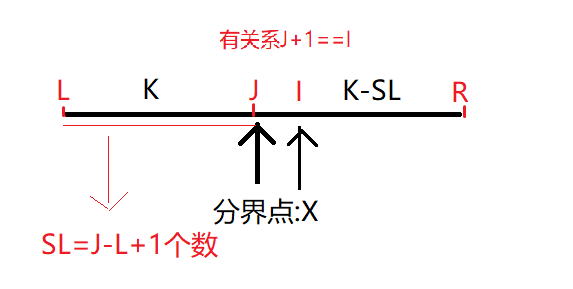
int sl=j-l+1;
if(sl>=k)
quick(l,j,k);
else
quick(j+1,r,k-sl);
}
int main()
{
int n,k;cin>>n>>k;
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
cout<<quick(0,n-1,k);
}
