查找算法之二分查找

参考

1. 二分查找法 | 博客园

二分查找

在有序的顺序表中查找元素，可以通过二分查找算法进行查找。

基本思想：

假设是递增序列（或者不减序列），

先通过待查找顺序表的最左端元素索引left 和最右端元素索引right求得中间元素索引middle（ middle=(left+right)/2 ），然后将待查元素与中间元素比较。若待查元素>中间元素，则右移left至middle+1在较大的子序列中继续查找；若待查元素<中间元素，则左移right至middle-1在较小的子序列中继续查找；如果待查元素=中间元素，则查找成功，返回当前位置索引middle即可；如果left==midle或者right==middle还未能查找到，则查找失败。

 即：

0) 结束条件：left > right，或者已查找到目标

1) 令mid = (left+right)/2

2) 如果value == a[mid], mid即为查找到的位置，返回mid

3) 如果 value < a[mid]，说明value只可能在位置[left, mid)。

那么，令right=mid-1，重新开始步骤1)进行查找。

4) 如果value > a[mid]，说明value只可能在位置(mid, right]。

那么，令left=mid+1，重新开始步骤1)进行查找。

先决条件：

1. 待查存储在顺序表中（数组，而非链表）；

2. 待查顺序表有序（递增，递减都可以，相邻元素相等也可以）

先看一组示例，待查找有序顺序表：array[8]={4,6,7,22,23,23,45,56}, 待查找元素t=45

步骤：

那么初始状态，left=0, right=7, => middle=(left+right)/2=3. 由array[middle]=22 < t, 右移left=middle+1=4.

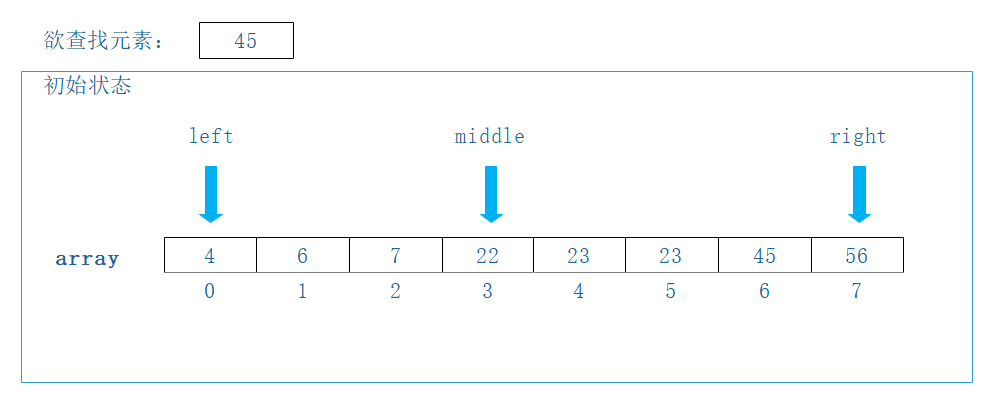
Step1, 重新求得middle=(left+right)/2=5,  由array[middle]=23 < t, 右移left=middle+1=6.

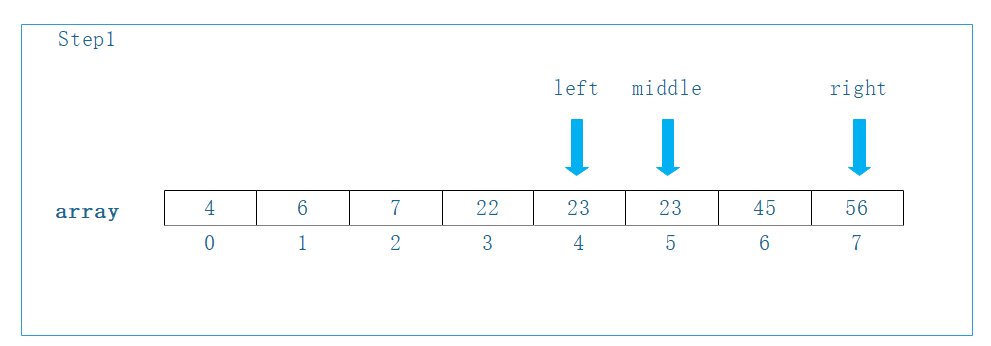
Step2, 重新求得middle=(left+right)/2=6,  由array[middle]=45== t. 查找成功，返回当前位置middle=6

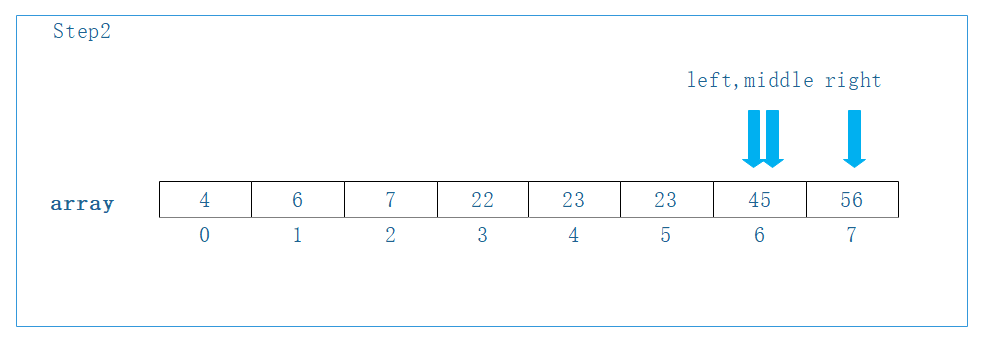
示例代码，为了便于快速验证、演示，用python进行编写

data = [4, 6, 7, 22, 23, 23, 45, 56] #all data to search


"""
bisearch(list, integer) -> integer
binary search for searching
@param arrary list to search
@param target element to search in the arrary
@return >=0 sucess
<0 failure
"""
def bisearch(array, target):
    left = 0
    right = len(array) - 1

    while left <= right:
        middle = (left + right) / 2
        if target > array[middle]:
            left = middle + 1
        elif target < array[middle]:
            right = middle - 1
        else:
            print 'find out %d in the arrays, index = %d.' %(target, middle)
            return middle
    print 'can not find out %d from the arrays.'%target
    return -1


print bisearch(data, 45) #sucess
print bisearch(data, 44) #failure

运行结果

find out 45 in the arrays, index = 6.
6
can not find out 44 from the arrays.
-1

二分查找变形

上述二分查找，是以查找待查值在递增（或递减）数组中的位置为目的，分为查找成功和不成功两种状态。有时候，即使查找不带待查值，也需要找到待查值在数组范围。

例子，某门课分x依据分数0,10,20,30,40,50,60,70,80,90,100分为A, B, C, D, E, F, G, H, I, J这10档，即

1）x=0 <=> A；

2）0<x<=10 <=>B；

3）10<x<=20 <=> C；

4）20<x<=30 <=> D；

5）30<x<=40 <=> E；

6）50<x<=60 <=> F；

3）60<x<=70<=> G；

3）70<x<=80<=> H；

3）80<x<=90<=> I；

3）90<x<=100<=> J；

现在要根据分数x，查找x所属成绩档。如何设计算法进行处理？