1. 怎样快速入门一个R包
这两天查看了十几个R包,也算是对看R入门一个R包有一些经验了把~
所有的R包都附带一个manual(有些R包还会有一个小manual,做简介用,那就更好了)。把manual下下来,看看它的最前面有没有一个对整个包general的介绍,如果有,那么一定要仔细阅读,这个非常重要!它会把整个包的大致情况介绍:要解决什么问题,用什么算法解决的......另外,它还会介绍最重要的函数(其实一个R包经常用到的函数不会一般超过五个!)了解这些信息,便很容易上手了~
但是并不是所有的R包都会有这样一个对本包的概述,对于这样的情况,可以在R包的主页上面找一个‘citation'的东西:这是与这个R包配套发表出来的论文。然后找到这篇论文后,去google拉,pubmed拉~~~搜一下把它下下来读一读就好了。当然,这个论文里面往往会有很多理论性特别强的大段公式,不过,看不懂跳过去就好,找到introduction,看看图基本就了解了!
总之,这两种方法配合起来使用入手一个R包还是蛮快的。
2. R 中的cluster包总结:
1)pvclust: 这个包是为hierarchical clustering的检测专门设计的,而且特别适合用在microarray的data上面,看到这篇论文的cited次数为300+就知道其受欢迎程度了。 这个包解决的问题就是:在microarray data中,sample数量是固定的,我们根据这个sample来做一个clustering,然后得出有几个cluster。可是,问题出来了:这些cluster都稳定么?你有没有想过如果在加进去几个sample的话你的cluster还会是这样?还是你的cluster就散掉了重新组成别的样子了。所以这个包提供了一个bootstrap resampling的方法来确定这个cluster是否稳定,并且在cluster上面表上相应的统计系数,还可以给robust的cluster套上红色长方形做标记。
值得注意的一点是,它的主函数pvclust是针对列,而默认的hclust函数却是针对行的,所以要想得到与hclust相同的结果一定要注意将matrix进行转置!
library('pvclust') library(car) mydata = na.omit(mtcars) #hierarchical clustering clustering # Ward Hierarchical Clustering d <- dist(t(mydata), method = "euclidean") # distance matrix fit <- hclust(d, method="ward") plot(fit, cex = .5) # normal hcluster dendrogram groups <- cutree(fit2, k=3) # cut tree into 3 clusters #draw dendogram with red borders around the 3 clusters rect.hclust(fit2, k=3, border="red") #pv cluster # Ward Hierarchical Clustering with Bootstrapped p values library(pvclust) fit2 <- pvclust(mydata, method.hclust="ward", method.dist="euclidean") plot(fit2, cex = .5) # display pv cluster dendogram # add rectangles around groups highly supported by the data pvrect(fit, alpha=.95) #alpha即为au值


可以看到,两个clust完全一样,只是pvclust的图有红色和绿色的图标,分别代表:
AU (Approximately Unbiased) p-value and BP (BootstrapProbability) value. AU p-value, which is computed by multiscale bootstrap resampling, is a better approximation to unbiased p-value than BP value computed by normal bootstrap resampling
2)mclust
这是一个model based clustering的包,与kmeans等聚类不同,mclust是基于统计模型的聚类:即假设不同的cluster来自不同的分布,而整个data则是一个mixed model 的分布。mclust提供几种模型,如multivariate normal distribution等等,根据几种不同的模型分别拟合data,利用特定算法找出相应的模型以及其对应的部分data。
library(mclust) fit <- Mclust(mydata) plot(fit) # plot results
这里会出现数张图,第一张是类似下图的一张图,每种颜色代表一个模型(具体什么还没仔细看),而mclust的任务就是找出哪个模型得到最大的BIC值(如图可见,VEV在四个group的时候BIC最大),即得到组数!第二张图则是如下右所示,是根据cluster的情况对数据进行lattice散点图:不同颜色代表不同的组,根据对角线上的参数确定横纵坐标。


不过mclust并不提供bootstrap的重抽样,所以并不好用bootstrap方法来判断一个cluster的稳定性。当然,会有其他度量来衡量其稳定性的。
3). flexclust
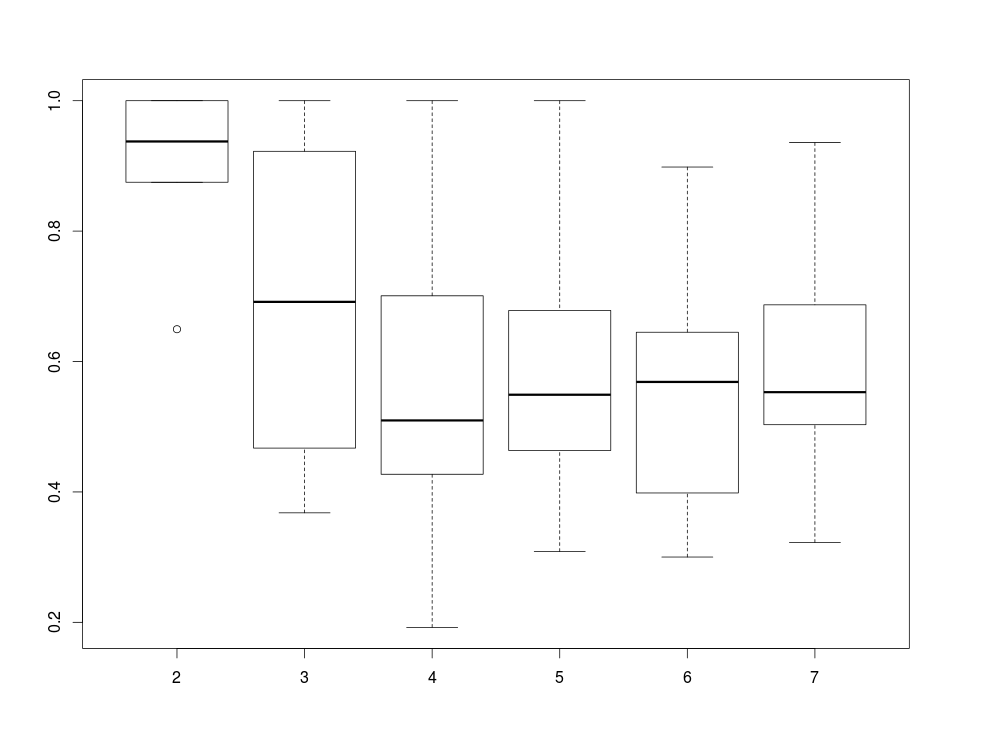
flexclust中主要函数有两个,第一个是bootFlexclust。这里重点说一下得出来的盒形图:其
横坐标为k值,纵坐标为RAND index,用来衡量cluster的稳定性:RAND Index = 1则说明cluster稳定,RAND Index = 0则说明cluster比较随机,通过这个盒形图可以看出cluster的趋势
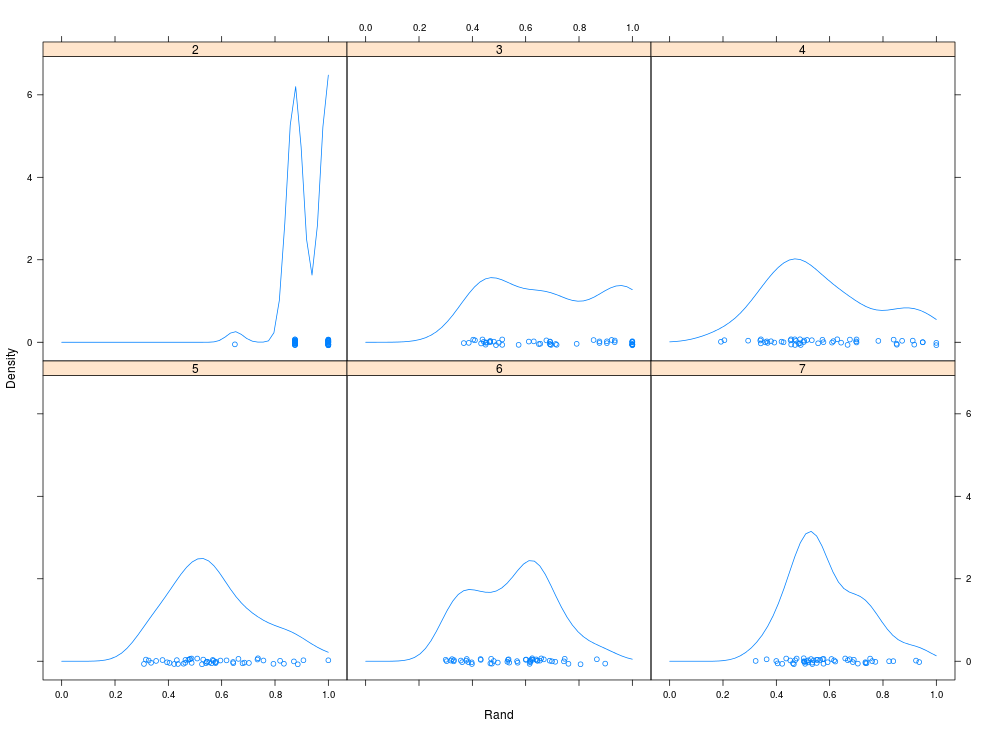
library('flexclust') x <- matrix(runif(400), ncol=2) cl <- FALSE #This is multi-core processor index ## 50 bootstrap replicates for speed in example, ## use more for real applications mydata = na.omit(mtcars) bcl <- bootFlexclust(mydata, k=2:7, nboot=50, FUN=cclust, multicore=cl) bcl #包含分组情况、一些index summary(bcl) #Rand index随k值(2-7)的分布情况 plot(bcl) #Rand Index随k值变化的盒形图:横坐标为k值,纵坐标为RAND index,用来衡量cluster的稳定性:RAND Index = 1则说明cluster稳定,RAND Index = 0则说明cluster比较随机 densityplot(bcl, from=0) #Rand Index随k值变化的密度图, 横坐标为RAND Index,纵坐标为密度 #compare with hclust plot(hclust(dist(mydata))) bcl summary(bcl)
另外一个常用函数为kcca
说是话感觉kcca和kmeans,pam什么的应该差不多,不知道它强在哪里,可能是它的做图功能把~
kcca1 = kcca(na.omit(mtcars), k=2)
kcca1
image(kcca1)
points(na.omit(mtcars))
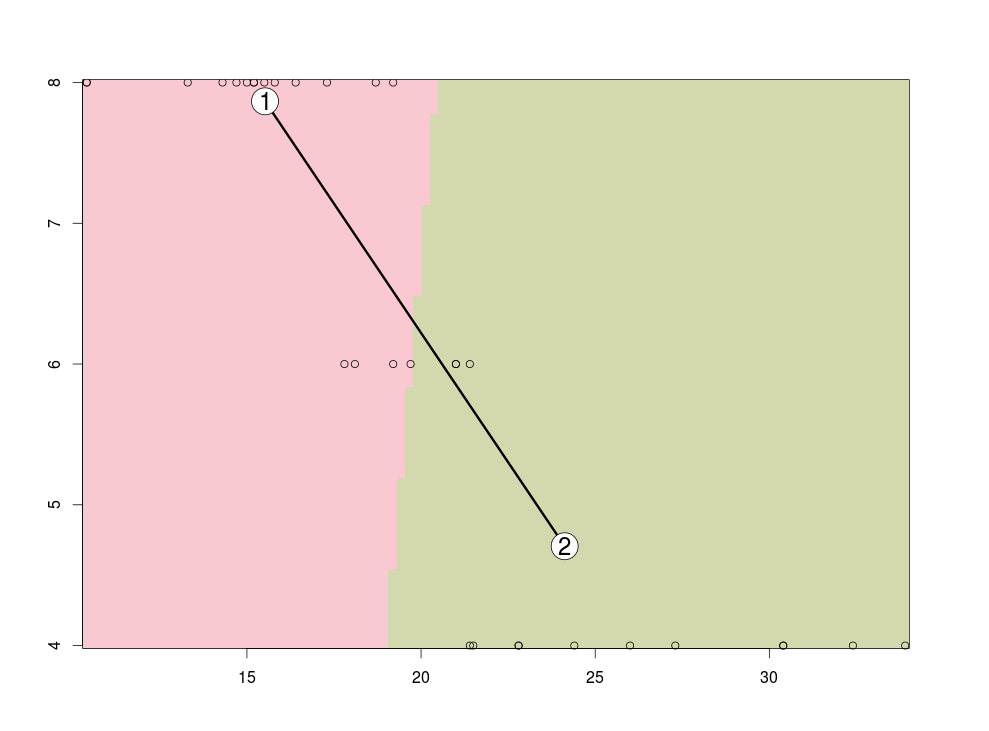
OK,今天先写这么多把~ 以后有用得着的话在写其他包~~贴一个R cluster资源汇总: