description:
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example:
Example 1:
nums1 = [1, 3]
nums2 = [2]
The median is 2.0
Example 2:
nums1 = [1, 2]
nums2 = [3, 4]
The median is (2 + 3)/2 = 2.5
my answer:
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size(), left = (m + n + 1) / 2, right = (m + n + 2) / 2;
return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;//这里是2.0!!!
}
int findKth(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
if (i >= nums1.size()) return nums2[j + k - 1];
if (j >= nums2.size()) return nums1[i + k - 1];
if (k == 1) return min(nums1[i], nums2[j]);
int midVal1 = (i + k / 2 - 1 < nums1.size()) ? nums1[i + k / 2 - 1] : INT_MAX;
int midVal2 = (j + k / 2 - 1 < nums2.size()) ? nums2[j + k / 2 - 1] : INT_MAX;
if (midVal1 < midVal2) {
return findKth(nums1, i + k / 2, nums2, j, k - k / 2);
} else {
return findKth(nums1, i, nums2, j + k / 2, k - k / 2);//这里必须是k-k/2,不要自作聪明写成k/2,比方说3-3/2=2 != 3/2=1
}
}
};
relative point get√:
- 二分法复习:
int SearchK(int *Arr,int low,int high,int k)
{
int mid;
while (low<high)
{
mid = (low + high) / 2;
if (Arr[mid] ==k){
return mid + 1;
}
else {
if (Arr[mid] < k){//右边查找
low = mid + 1;
}
else{
high = mid - 1;
}
}
}
cout << "未找到" << endl;
return -1;//没找到
}
hint :
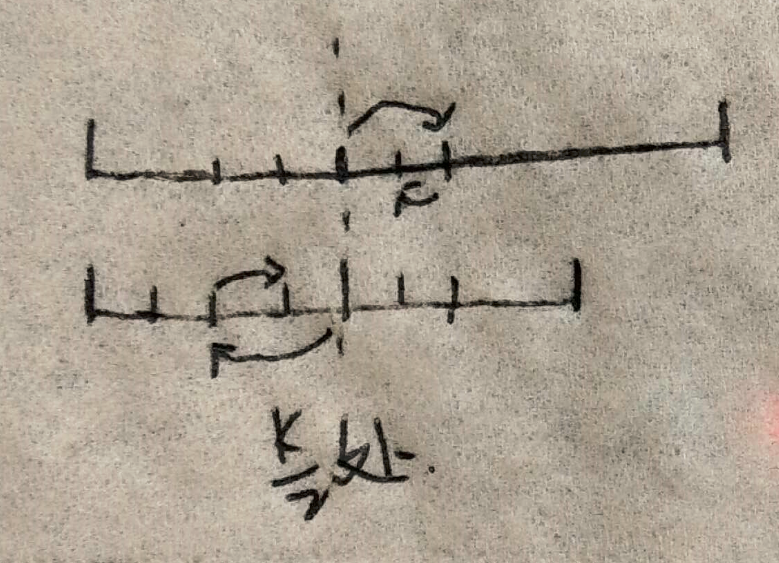
形象来讲就是上面这个图,先不考虑特殊情况。首先根据二者的长度能确定出中位数应该所在的位置k = [(m+n+1) / 2 + (m+n+2) / 2] / 2, 接下来的任务就是在两个array里都从最左边开始撸,一边整点最后凑足k个数,就知道从小到大排列数第k个数是谁了。这个图 中的 k/2 的位置就是两个array分别的开始比的地方,图里是假设第一回第一个数比第二个数小,那么第一个数就往大了挪点(挪之前距离的一半就是 k/4),第二个数就往小了挪点;第二回合的时候第一个数比较大了,那它就再往回挪点, 另一个就往大了挪,反正两个人就一个大了另一个就得小,因为他俩的总和一直必须得凑成k,就看最后第k个是谁。思维就是类似于数学中的求根的时候的二分法快速逼近。
之后特殊情况的话就是一个一直大另一个一直小,然后小没了,这个时候做个判断之后就直接找出来就行了。还有就是得判断判断这个数还能不能挪这些,其实都是挪出去了的问题,意思差不多。