环形链表（找到入口）（弗洛伊德算法）

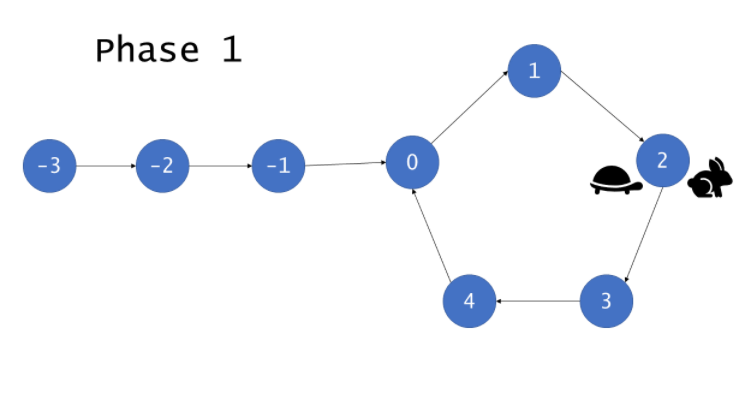
第一阶段：判断是否有环

第二阶段：判断入环口在哪里

 

/**
     * 双指针 时间复杂度 O(n) 空间复杂度 O(1)
     *
     * 先用双指针法判断链表是否有环，若有则返回第一次相遇的节点
     *
     * 第一次相遇时，假设【慢指针】 slow 走了 k 步，那么快指针 fast 一定走了 2k 步，
     * 也就是说比 slow 多走了 k 步（也就是环的长度）。
     *
     * 设【相遇点】距【环的起点】的距离为 m，
     *      那么【环的起点】距【头结点】 head 的距离为 k - m，（慢指针是第一次走到这）
     * 也就是说如果从 head 前进 k - m 步就能到达环起点。
     * 巧的是，如果从相遇点继续前进 k - m 步，也能再次到达环起点。
     *
     * 所以，我们让一个指针从起点出发，另一个指针从相遇点出发，二者速度相同，相遇时，就到达了环的起点
     *
     * @param head
     * @return
     */
    public ListNode detectCycle2(ListNode head) {
        // 找到快慢指针相遇的节点
        ListNode intersect = hasCycle(head);
        // 说明无环
        if (intersect == null) return null;
        // 一个指针从head出发，一个指针从相遇点出发，速度相同
        // 二者相遇时的地点，即为环的起点
        while (head != intersect) {
            head = head.next;
            intersect = intersect.next;
        }
        return head;
    }

    /**
     * 双指针法判断链表是否有环 时间复杂度 O(n) 空间复杂度 O(1)
     * 
     * 有则返回快慢指针第一次相遇的节点，无则返回null
     *
     * @param head
     * @return
     */
    public ListNode hasCycle(ListNode head) {
        // 只有一个节点
        if (head == null || head.next == null) return null;
        // 同时出发
        ListNode fast = head, slow = head;
        // 快指针速度是慢指针二倍
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            // 最终相遇
            if (fast == slow) return fast;
        }
        return null;
    }

可以这样解释性地来理解阶段2：

1. 快指针1次走2步，慢指针1次走1步。所以快指针总是走了慢指针两倍的路。
2. 回顾一下阶段1的过程，设头节点到入环点的路途为 n, 那么慢指针走了入环路途的一半（n/2）时，快指针就到达入环点了(走完n了)。
3. 慢指针再继续走完剩下的一般入环路途（剩下的n/2），到达入环点时，快指针已经在环内又走了一个 n 那么远的路了。
4. 为了方便理解，这里先讨论环很大，大于n的情况（其他情况后文补充）。此时，慢指针正处于入环点，快指针距离入环点的距离为n。环内路，可以用此时快指针的位置分割为两段，前面的 n 部分，和后面的 b 部分。
5. 此时开始继续快慢指针跑圈，因为已经在环内了，他们其实就是在一条nbnbnbnbnbnbnb（无尽nb路）上跑步。
6. 慢指针从入环处开始跑b步，距离入环处就剩下了n。此时，快指针则是从距离入环处n步远的位置开始跑了2b步，距离入环处也是剩下了n。他们相遇了，并且距离入环处的距离就是n，n就是头节点到入环点的距离阿!!!