[剑指Offer] 4 二维数组中的查找

题目：二维数组中的查找

描述

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。
请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

思路

根据二维数组递增的特性，查找的形式如下：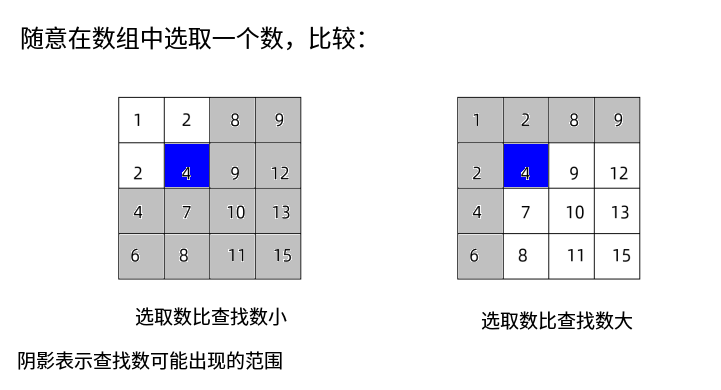

• 暴力破解可以解决问题
  按行遍历，直到等于查找数/大于查找数/越界

• 可以从边界出发
  利用特性，可以确定一整列或整行的是否在查找范围
  比如：从右上角出发，第一个数字表示该列的最小值，该行最大值
  如果查找数比该列最小值还小，则表示该列不在查找范围
  如果查找数比该行最大值还大，则表示该行不在查找范围
  

类似递归方法，每次都在缩减数据规模，将问题转化为更小的同样性质的问题

/*******************************************************************
Copyright(c) 2016, Harry He
All rights reserved.

Distributed under the BSD license.
(See accompanying file LICENSE.txt at
https://github.com/zhedahht/CodingInterviewChinese2/blob/master/LICENSE.txt)
*******************************************************************/

//==================================================================
// 《剑指Offer——名企面试官精讲典型编程题》代码
// 作者：何海涛
//==================================================================

// 面试题4：二维数组中的查找
// 题目：在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按
// 照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个
// 整数，判断数组中是否含有该整数。

#include <cstdio>
#if 0
bool Find(int* matrix, int rows, int columns, int number)
{
    bool found = false;

    if (matrix != nullptr && rows > 0 && columns > 0)
    {
        int row = 0;
        int column = columns - 1;
        while (row < rows && column >= 0)
        {
            if (matrix[row * columns + column] == number)
            {
                found = true;
                break;
            }
            else if (matrix[row * columns + column] > number)
                --column;
            else
                ++row;
        }
    }

    return found;
}


//从右上角开始
bool Find(int* matrix, int rows, int columns, int number)
{
    bool result = false;

    int row = 0;
    int column = columns - 1 ;
    int tmp;
    // row>=rows ;column < 0 蕴含着自动终止条件，找不到正确的值，可以自动退出while,平时while写的太少了
    while (matrix != nullptr && row < rows && column >= 0)
    {
        tmp = matrix[row*columns + column];

        if (tmp > number)
        {
            column--;
        }
        else if (tmp < number)
        {
            row++;
        }
        else
        {
            result = true;
            // 为什么要有break,成立之后，row column不更新，跳不出while
            break;
        }
    }
    


    return result;
}
#endif
//从左下角开始
bool Find(int* matrix, int rows, int columns, int number)
{
    bool result = false;

    int row = rows-1;
    int column = 0;
    int tmp;
    // row>=rows ;column < 0 蕴含着自动终止条件，找不到正确的值，可以自动退出while,平时while写的太少了
    //while (matrix != nullptr && row < rows && column >= 0)
    while (matrix != nullptr && row>=0  && column < columns )
    {
        tmp = matrix[row*columns + column];

        if (tmp > number)
        {
            row--;
        }
        else if (tmp < number)
        {
            column++;
        }
        else
        {
            result = true;
            // 为什么要有break,成立之后，row column不更新，跳不出while
            break;
        }
    }



    return result;
}

// ====================测试代码====================
void Test(char* testName, int* matrix, int rows, int columns, int number, bool expected)
{
    if (testName != nullptr)
        printf("%s begins: ", testName);

    bool result = Find(matrix, rows, columns, number);
    if (result == expected)
        printf("Passed.
");
    else
        printf("Failed.
");
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数在数组中
void Test1()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test1", (int*)matrix, 4, 4, 7, true);
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数不在数组中
void Test2()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test2", (int*)matrix, 4, 4, 5, false);
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数是数组中最小的数字
void Test3()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test3", (int*)matrix, 4, 4, 1, true);
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数是数组中最大的数字
void Test4()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test4", (int*)matrix, 4, 4, 15, true);
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数比数组中最小的数字还小
void Test5()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test5", (int*)matrix, 4, 4, 0, false);
}

//  1   2   8   9
//  2   4   9   12
//  4   7   10  13
//  6   8   11  15
// 要查找的数比数组中最大的数字还大
void Test6()
{
    int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
    Test("Test6", (int*)matrix, 4, 4, 16, false);
}

// 鲁棒性测试，输入空指针
void Test7()
{
    Test("Test7", nullptr, 2, 2, 16, false);
}

int main(int argc, char* argv[])
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    Test6();
    Test7();

    return 0;
}