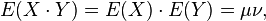摘录wiki如下(红色字体是特别标注的部分):
http://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE
协方差
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为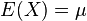 与
与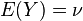 的两个实数随机变量X 与Y 之间的协方差定义为:
的两个实数随机变量X 与Y 之间的协方差定义为:
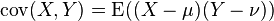 ,
,
其中E是期望值。它也可以表示为:
 ,
,
直观上来看,协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X 与Y 是统计独立的,那么二者之间的协方差就是0,这是因为
但是反过来并不成立,即如果X 与Y 的协方差为0,二者并不一定是统计独立的。只能说是线性无关
取决于协方差的相关性η(这东西又叫皮尔逊系数,参见另一篇博文)
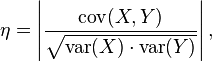 =E(XY)/√EX2√EY2
=E(XY)/√EX2√EY2
更准确地说是线性相关性,是一个衡量线性独立的无量纲数,其取值在[0,+1]之间。相关性η = 1时称为“完全线性相关”,此时将Yi对Xi作Y-X 散点图,将得到一组精确排列在直线上的点;相关性数值介于0到1之间时,其越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。
相关性为0(因而协方差也为0)的两个随机变量又被称为是不相关的,或者更准确地说叫作“线性无关”、“线性不相关”,这仅仅表明X 与Y 两随机变量之间没有线性相关性,并非表示它们之间一定没有任何内在的(非线性)函数关系,和前面所说的“X、Y二者并不一定是统计独立的”说法一致。
如果要用公式写一下的话,注意,当X,Y是线性相关的变量时(均去中心化,那么Y和X就是倍数关系),Y=aX。截距b被去中心化了
对η还是要再说明一下:这个东西是衡量X,Y的线性相关程度的。也可以通俗的讲,η衡量的是X,Y的关系有“多像”线性相关。也就是说它是从线性相关的角度来观察X和Y的。如果XY就是线性相关的,那自然η就是1,确实“很像”;但如果XY是其他相关,比如对数相关y=log(x)y之类的,η也是衡量这个对数相关有“多像”线性相关。更深究一点,衡量有“多像”这个事情,实际上是衡量Y与X的变化趋势是否保持一致,比如x扩大几倍,y也扩大几倍。倍数越不一样说明越不像线性相关。
属性
如果X 与Y 是实数随机变量,a 与b 不是随机变量,那么根据协方差的定义可以得到:
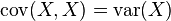 ,
,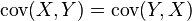 ,
, ,
,
对于随机变量序列X1, ..., Xn与Y1, ..., Ym,有
 ,
,
对于随机变量序列X1, ..., Xn,有
 。
。
协方差矩阵[编辑]
分别为m 与n 个标量元素的列向量随机变量X 与Y,二者对应的期望值分别为μ与ν,这两个变量之间的协方差定义为m×n 矩阵
两个向量变量的协方差cov(X, Y)与cov(Y, X)互为转置矩阵。