05 线性代数

1 只由一个元素组成的张量称为一维张量

x=torch.tensor([3.0])
y=torch.tensor([2.0])
x+y,x-y,x*y,x/y,x**y

(tensor([5.]), tensor([1.]), tensor([6.]), tensor([1.5000]), tensor([9.]))

2 矩阵的转置

A=torch.arange(20).reshape(5,4)
A

tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

A.T

tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])

3 拷贝内容到新的内存

C=A    #这里没有拷贝，只是将A的指针直接给了C
B=A.clone() #将A的内容拷贝到新的内存给B
C[:]=1  #改变了A所指的数据
A,B,C

(tensor([[1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1]]),
 tensor([[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11],
         [12, 13, 14, 15],
         [16, 17, 18, 19]]),
 tensor([[1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1],
         [1, 1, 1, 1]]))

4 对矩阵元素求和

A=torch.arange(40).reshape(2,5,4)
A

tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11],
         [12, 13, 14, 15],
         [16, 17, 18, 19]],

        [[20, 21, 22, 23],
         [24, 25, 26, 27],
         [28, 29, 30, 31],
         [32, 33, 34, 35],
         [36, 37, 38, 39]]])

A.shape,A.sum()

(torch.Size([2, 5, 4]), tensor(780))

A.sum().shape

torch.Size([])

5 按特定轴求和

A_sum_axis0=A.sum(axis=0)
A_sum_axis0,A_sum_axis0.shape

(tensor([[20, 22, 24, 26],
         [28, 30, 32, 34],
         [36, 38, 40, 42],
         [44, 46, 48, 50],
         [52, 54, 56, 58]]),
 torch.Size([5, 4]))

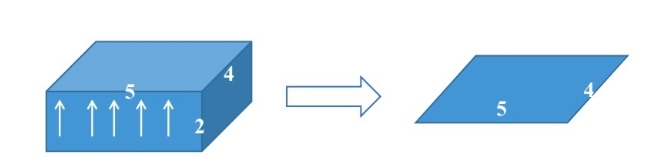
A是2*5*4，axis=0表示将2这一维度压缩掉，最后变成了5*4，如下图所示

A_sum_axis1=A.sum(axis=1)
A_sum_axis1,A_sum_axis1.shape

(tensor([[ 40,  45,  50,  55],
         [140, 145, 150, 155]]),
 torch.Size([2, 4]))

axis=1时则变成了2*4

A_sum_axis2=A.sum(axis=2)
A_sum_axis2,A_sum_axis2.shape

(tensor([[  6,  22,  38,  54,  70],
         [ 86, 102, 118, 134, 150]]),
 torch.Size([2, 5]))

axis=2时则变成了2*5

可以让keepdims参数变成True来让维度不变----压缩掉的那维变成1-------方便进行广播。

A_sum_axis0=A.sum(axis=0,keepdims=True)
A_sum_axis0,A_sum_axis0.shape

(tensor([[[20, 22, 24, 26],
          [28, 30, 32, 34],
          [36, 38, 40, 42],
          [44, 46, 48, 50],
          [52, 54, 56, 58]]]),
 torch.Size([1, 5, 4]))

注意可以同时压缩掉两个维度

A_sum_axis0_1=A.sum(axis=[0,1],keepdims=True)
A_sum_axis0_1,A_sum_axis0_1.shape

(tensor([[[180, 190, 200, 210]]]), torch.Size([1, 1, 4]))

6 向量的点积和

  这里表示相同位置元素乘积之和，不同数据类型不能进行点积运算，dot也只能进行一维向量的点积。

x=torch.arange(4,dtype=torch.float32)
y=torch.ones(4,dtype=torch.float32)
torch.dot(x,y)

tensor(6.)

print(x*y)  #元素乘法
sum(x*y)

tensor([0., 1., 2., 3.])

tensor(6.)

7 torch.mv()

  表示矩阵（二维）与向量（一维）之间的乘积，且数据类型必须相同

K=torch.tensor([[ 0.0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11],
         [12, 13, 14, 15],
         [16, 17, 18, 19]])
K.shape,x.shape,torch.mv(K,x)

(torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

8 torch.mm()

  表示矩阵（二维）与矩阵（二维）之间的乘积，且数据类型必须相同

9 范数

  范数表示矩阵或者向量的长度。

（1） L₂范数

    

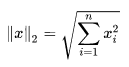
      L₂范数   主要是针对向量的

u=torch.tensor([3.0,-4.0])
torch.norm(u)

tensor(5.)

（2）L1范数
表示元素绝对值的和

torch.abs(u).sum()

tensor(7.)
（3）弗罗贝尼乌斯范数(  )

这是针对矩阵的，表示矩阵元素和的平方值开方，与L2范数类似

Z=torch.ones(4,9)
torch.norm(Z)

tensor(6.)