如何实现文本编辑器中的查找替换功能？——BF算法

1 BM（Boyer-Moore）算法

  它是一种非常高效的字符串匹配算法，有实验统计，它的性能是著名的KMP算法的 3 到 4 倍。BM 算法核心思想是，利用模式串本身的特点，在模式串中某个字符与主串不能匹配的时候，将模式串往后多滑动几位，以此来减少不必要的字符比较，提高匹配的效率。BM 算法构建的规则有两类，坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存，为了节省内存，我们可以只用好后缀规则来实现 BM 算法。

1.1 坏字符规则

  BM 算法的匹配顺序比较特别，它是按照模式串下标从大到小的顺序，倒着匹配的。我画了一张图，你可以看下。我们从模式串的末尾往前倒着匹配，当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符（主串中的字符）。

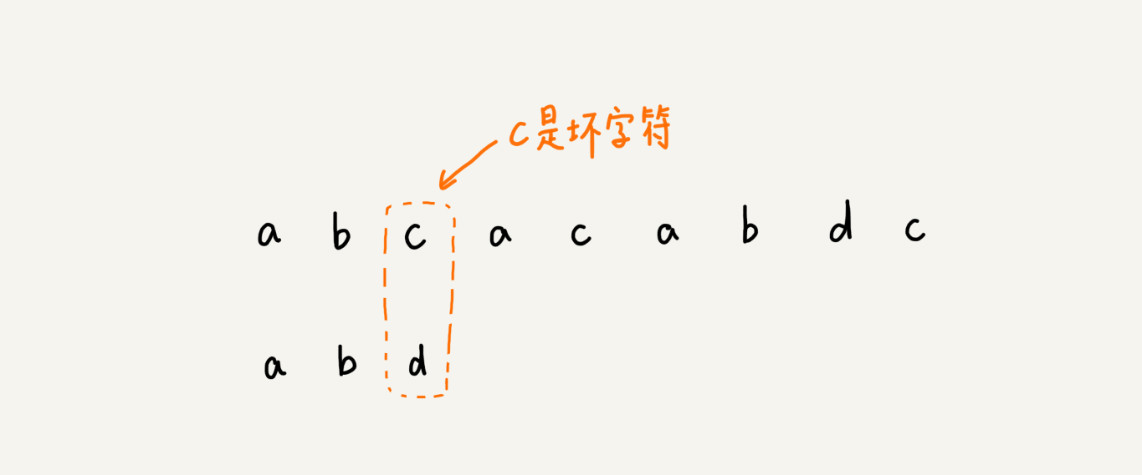
1.2 好后缀规则

  好后缀规则实际上跟坏字符规则的思路很类似。你看我下面这幅图。当模式串滑动到图中的位置的时候，模式串和主串有 2 个字符是匹配的，倒数第 3 个字符发生了不匹配的情况。

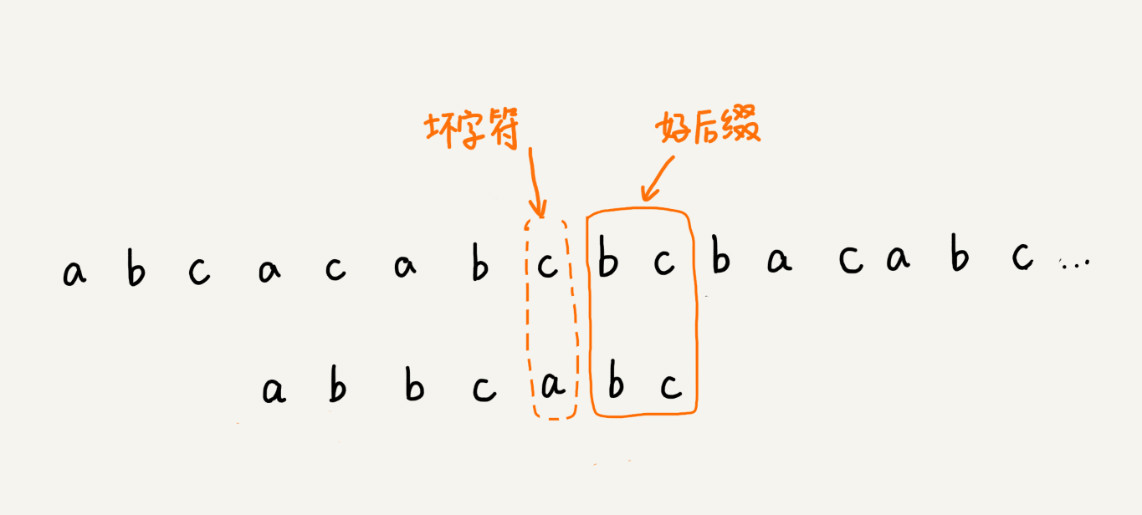
  好后缀的处理规则中最核心的内容：

• 在模式串中，查找跟好后缀匹配的另一个子串；

• 在好后缀的后缀子串中，查找最长的、能跟模式串前缀子串匹配的后缀子串；

2 各部分代码如下

#include <iostream>
#include <math.h>
#include <cstring>
using namespace std;

#define MAXNUM 256

// 计算坏字符对应的hashtable
void generateHashTable(char b[], int m, int hashtable[]){
    for(int i = 0; i < m; i++){
        int ascii = (int)b[i];
        // 这样写是可以的，会将坏字符放在最右边儿的位置
        hashtable[ascii] = i;
    }
}

int moveByGS(int j, int m, int suffix[], bool prefix[]){
    // 好后缀长度
    int k = m - 1 - j;
    if(suffix[k] != -1)
        return j - suffix[k] + 1;
    for(int r = j + 2; r <= m - 1; r++){
        if(prefix[m - r])
            return r;
    }
    return m;
}

// 计算好后缀对应的数组
void generateGS(char b[], int m, int suffix[], bool prefix[]){
    // b[0, i]
    for(int i = 0; i < m - 1 ; i++){
        int j = i;
        // 公共后缀串长度
        int k = 0;
        // 妙啊
        while(j >= 0 && b[j] == b[m - 1 - k]){
            j--;
            k++;
            suffix[k] = j + 1;
        }
        if(j == -1)
            prefix[k] = true;
    }
}

// BF算法
int boyerMoore(char a[], int n, char b[], int m){
    // 根据模式串生成hashtable
    int hashtable[MAXNUM + 1];
    // 初始化
    memset(hashtable, -1, sizeof(hashtable));
    generateHashTable(b, m, hashtable);

    // 根据模式串生成suffix、prefix
    int suffix[MAXNUM + 1];
    bool prefix[MAXNUM + 1];
    memset(suffix, -1, sizeof(suffix));
    memset(prefix, false, sizeof(prefix));
    generateGS(b, m, suffix, prefix);
    int i = 0;
    while(i <= n - m){
        int j;
        // BF算法从后往前匹配
        for(j = m - 1; j >= 0; j--){
            // 找到坏字符
            if(a[i + j] != b[j])
                break;
        }
        if(j < 0)
            return i;
        // 找到坏字符在模式串中的位置
        int x = j - hashtable[(int)a[i+j]];
        /***********好后缀方法************/
        int y = 0;
        // 如果有好后缀
        if(j < m - 1)
            y = moveByGS(j, m, suffix, prefix);
        i = i + max(x, y);
    }
    return -1;
}