博客转载自：http://www.cnblogs.com/21207-iHome/p/6133072.html
扩展卡尔曼滤波的状态方程和观测方程可以是非线性的。在一般情况下，无法确定过程噪声、测量噪声与方程的函数关系，因此可以简化为加性噪声：
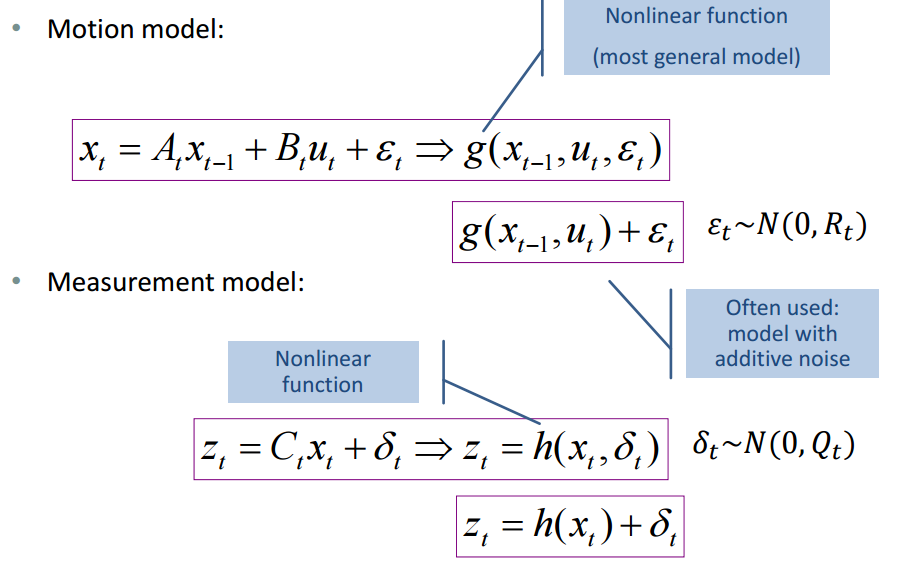
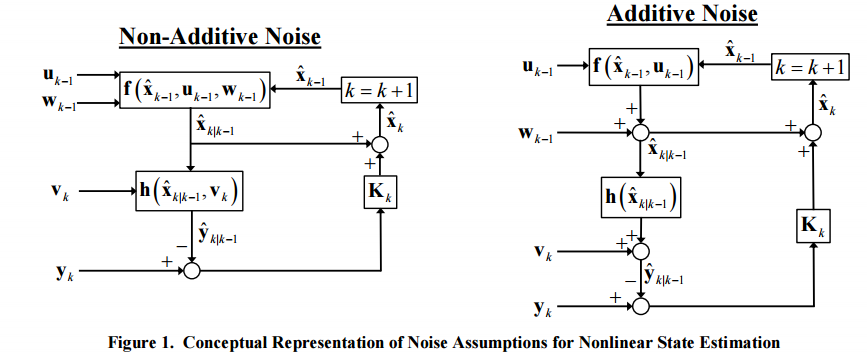
EKF relies on a linearisation of the evolution and observation functions which are good approximations of the original functions if these functions are close to linear. The state-space formulation of EKF reads :
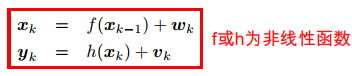
Non-linear evolution and observation functions are handled within EKF by linearising these functions around some estimates of the state; for example for the evolution function is linearized around the previous estimate of the state x^kx^k:
The first step in applying EKF is to linearize the evolution function around the previous estimate of the state x^k−1x^k−1
扩展卡尔曼滤波流程如下图所示：
一个简单的例子：假设一架飞机以恒定水平速度飞行（高度不变），地面上有一个雷达可以发射电磁波测量飞机到雷达的距离rr。则有如下关系：
θ=arctan(yx)θ=arctan(yx) r2=x2+y2r2=x2+y2
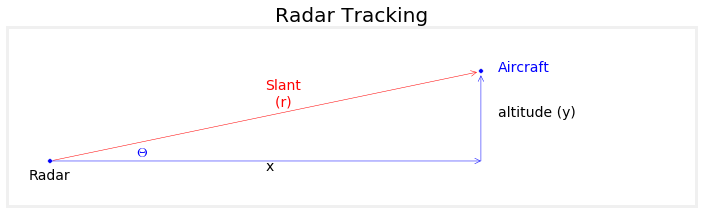
我们想知道某一时刻飞机的水平位置和垂直高度，以水平位置、水平速度、垂直高度作为状态变量：
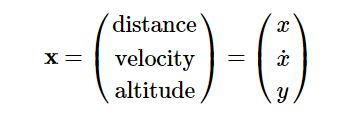
则观测值与状态变量之间的关系为：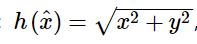
，可以看出这是一个非线性的表达式。对于这个问题来说，观测方程的雅克比矩阵为：
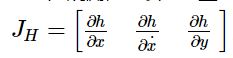，即
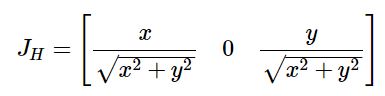
状态转移方程的雅克比矩阵为：
得到上述矩阵后我们就可以设定初值和噪声，然后根据流程图中的步骤进行迭代计算。
MRPT中的卡尔曼滤波器
卡尔曼滤波算法都集中在 mrpt::bayes::CKalmanFilterCapable这个虚类中。 这个类中包括系统状态向量和系统协方差矩阵，以及根据选择的算法执行一个完整迭代的通用方法。在解决一个特定问题时需要从这个虚类派生一个新的类，并实现状态转移函数、观测函数以及它们的雅克比矩阵(采用EKF时)。内部的mrpt::bayes::CKalmanFilterCapable::runOneKalmanIteration()函数会依次调用用户改写的虚函数，每调用一次该函数执行一步预测+校正操作（runOneKalmanIteration():The main entry point, executes one complete step: prediction + update）
使用MRPT解决上述问题的C++代码如下：
#include <mrpt/bayes/CKalmanFilterCapable.h>
#include <mrpt/random.h>
#include <mrpt/system/os.h>
#include <mrpt/system/threads.h>
#include <iostream>
using namespace mrpt;
using namespace mrpt::bayes;
using namespace mrpt::math;
using namespace mrpt::utils;
using namespace mrpt::random;
using namespace std;
#define DELTA_TIME 0.05f // Time Step between Filter Steps
// 系统状态变量初始值(猜测值)
#define VEHICLE_INITIAL_X 10.0f
#define VEHICLE_INITIAL_Y 2000.0f
#define VEHICLE_INITIAL_V 200.0f
#define TRANSITION_MODEL_STD 1.0f // 模型噪声
#define RANGE_SENSOR_NOISE_STD 5.0f // 传感器噪声
/* --------------------------------------------------------------------------------------------
Virtual base for Kalman Filter (EKF,IEKF,UKF) implementations.
template<size_t VEH_SIZE, size_t OBS_SIZE, size_t FEAT_SIZE, size_t ACT_SIZE, typename KFTYPE>
class mrpt::bayes::CKalmanFilterCapable< VEH_SIZE, OBS_SIZE, FEAT_SIZE, ACT_SIZE, KFTYPE >
The meaning of the template parameters is:
VEH_SIZE: The dimension of the "vehicle state"(系统状态变量数目)
OBS_SIZE: The dimension of each observation (eg, 2 for pixel coordinates, 3 for 3D coordinates,etc).(观测量维数)
FEAT_SIZE: The dimension of the features in the system state (the "map"), or 0 if not applicable (the default if not implemented).
ACT_SIZE: The dimension of each "action" u_k (or 0 if not applicable).(控制量的维数)
KFTYPE: The numeric type of the matrices (default: double)
This base class stores the state vector and covariance matrix of the system. It has virtual methods
that must be completed by derived classes to address a given filtering problem.
---------------------------------------------------------------------------------------------- */
// Implementation of the system models as a EKF
class CRange: public CKalmanFilterCapable<3, 1, 0, 0>
{
public:
CRange( );
virtual ~CRange();
void Process( double DeltaTime, double observationRange);
void getState( KFVector &xkk, KFMatrix &pkk)
{
xkk = m_xkk; //The system state vector.
pkk = m_pkk; //The system full covariance matrix
}
protected:
float m_obsRange; // 观测值
float m_deltaTime; // Time Step between Filter Steps
// return the action vector u
void OnGetAction( KFArray_ACT &out_u ) const;
// Implements the transition model
void OnTransitionModel(const KFArray_ACT &in_u,KFArray_VEH &inout_x,bool &out_skipPrediction) const;
// Implements the transition Jacobian
void OnTransitionJacobian(KFMatrix_VxV &out_F ) const;
// Implements the transition noise covariance
void OnTransitionNoise(KFMatrix_VxV &out_Q ) const;
// Return the observation NOISE covariance matrix, that is, the model of the Gaussian additive noise of the sensor.
void OnGetObservationNoise(KFMatrix_OxO &out_R) const;
/** This is called between the KF prediction step and the update step
* This method will be called just once for each complete KF iteration.
*
ote It is assumed that the observations are independent, i.e. there are NO cross-covariances between them.
*/
void OnGetObservationsAndDataAssociation(
vector_KFArray_OBS &out_z,
mrpt::vector_int &out_data_association,
const vector_KFArray_OBS &in_all_predictions,
const KFMatrix &in_S,
const vector_size_t &in_lm_indices_in_S,
const KFMatrix_OxO &in_R
);
// Implements the observation prediction
void OnObservationModel(const vector_size_t &idx_landmarks_to_predict,vector_KFArray_OBS &out_predictions) const;
// Implements the observation Jacobians
void OnObservationJacobians(const size_t &idx_landmark_to_predict,KFMatrix_OxV &Hx,KFMatrix_OxF &Hy) const;
};
CRange::CRange()
{
KF_options.method = kfEKFNaive;
// 状态变量初始值 State: (x,vx,y)
m_xkk.resize(3); //对于动态矩阵可以通过resize()函数来动态修改矩阵的大小
m_xkk[0]= VEHICLE_INITIAL_X;
m_xkk[1]= VEHICLE_INITIAL_V;
m_xkk[2]= VEHICLE_INITIAL_Y;
// Initial cov: Large uncertainty
m_pkk.setSize(3,3);
m_pkk.unit();
m_pkk = 50 * m_pkk;
}
CRange::~CRange()
{
}
void CRange::Process( double DeltaTime, double observationRange)
{
m_deltaTime = (float)DeltaTime;
m_obsRange = (float)observationRange;
runOneKalmanIteration(); // executes one complete step: prediction + update
}
// Must return the action vector u.
// param out_u: The action vector which will be passed to OnTransitionModel
void CRange::OnGetAction( KFArray_ACT &out_u ) const
{
}
/** Implements the transition model(Project the state ahead)
param in_u : The vector returned by OnGetAction.
param inout_x: prediction value
param out_skip: Set this to true if for some reason you want to skip the prediction step. Default:false
*/
void CRange::OnTransitionModel(const KFArray_ACT &in_u, KFArray_VEH &inout_x, bool &out_skipPrediction) const
{
// The constant-velocities model is implemented simply as:
inout_x[0] += m_deltaTime * inout_x[1];
inout_x[1] = inout_x[1];
inout_x[2] = inout_x[2];
}
/** Implements the transition Jacobian
param out_F Must return the Jacobian.
The returned matrix must be N*N with N being the size of the whole state vector.
*/
void CRange::OnTransitionJacobian(KFMatrix_VxV &F) const
{
F.unit();
F(0,1) = m_deltaTime;
}
/** Implements the transition noise covariance
param out_Q Must return the covariance matrix.
The returned matrix must be of the same size than the jacobian from OnTransitionJacobian
*/
void CRange::OnTransitionNoise(KFMatrix_VxV &Q) const
{
Q.unit();
Q *= square(TRANSITION_MODEL_STD);
}
/** Return the observation NOISE covariance matrix, that is, the model of the Gaussian additive noise of the sensor.
param out_R : The noise covariance matrix. It might be non diagonal, but it'll usually be.
*/
void CRange::OnGetObservationNoise(KFMatrix_OxO &R) const
{
R.unit();
R *= square(RANGE_SENSOR_NOISE_STD);
}
// This is called between the KF prediction step and the update step
void CRange::OnGetObservationsAndDataAssociation(
vector_KFArray_OBS &out_z,
mrpt::vector_int &out_data_association,
const vector_KFArray_OBS &in_all_predictions,
const KFMatrix &in_S,
const vector_size_t &in_lm_indices_in_S,
const KFMatrix_OxO &in_R
)
{
//out_z: N vectors, N being the number of "observations"
out_z.resize(1);
out_z[0][0] = m_obsRange;
}
/** Implements the observation prediction
param idx_landmark_to_predict: The indices of the landmarks in the map whose predictions are expected as output. For non SLAM-like problems, this input value is undefined and the application should just generate one observation for the given problem.
param out_predictions: The predicted observations.
*/
void CRange::OnObservationModel(const vector_size_t &idx_landmarks_to_predict,vector_KFArray_OBS &out_predictions) const
{
// idx_landmarks_to_predict is ignored in NON-SLAM problems
out_predictions.resize(1);
out_predictions[0][0] = sqrt( square(m_xkk[0]) + square(m_xkk[2]) );
}
// Implements the observation Jacobians
void CRange::OnObservationJacobians(const size_t &idx_landmark_to_predict,KFMatrix_OxV &Hx,KFMatrix_OxF &Hy) const
{
Hx.zeros();
Hx(0,0) = m_xkk[0] / sqrt(square(m_xkk[0])+square(m_xkk[2]));
Hx(0,2) = m_xkk[2] / sqrt(square(m_xkk[0])+square(m_xkk[2]));
}
int main ()
{
// Create class instance
CRange EKF;
EKF.KF_options.method = kfEKFNaive; //select the KF algorithm
// Initiate simulation
float x=0, y=1000, v=100; //状态变量真实值
float t=0;
while (!mrpt::system::os::kbhit())
{
// Simulate noisy observation:
x += v * DELTA_TIME;
float realRange = sqrt(square(x)+square(y));
// double mrpt::random::CRandomGenerator::drawGaussian1D_normalized(double * likelihood = NULL)
// Generate a normalized (mean=0, std=1) normally distributed sample
float obsRange = max(0.0, realRange + RANGE_SENSOR_NOISE_STD * randomGenerator.drawGaussian1D_normalized() );
printf("Real/Simulated range: %.03f / %.03f
", realRange, obsRange );
// Process with EKF
EKF.Process(DELTA_TIME, obsRange);
// Show EKF state:
CRange::KFVector EKF_xkk;
CRange::KFMatrix EKF_pkk;
EKF.getState( EKF_xkk, EKF_pkk );
printf("Real state: x:%.03f v=%.03f y=%.03f
",x,v,y);
cout << "EKF estimation:" <<endl<< EKF_xkk << endl;
cout <<"-------------------------------------------"<<endl;
// Delay(An OS-independent method for sending the current thread to "sleep" for a given period of time)
mrpt::system::sleep((int)(DELTA_TIME*1000));
t += DELTA_TIME;
}
return 0;
}
运行一段时间后结果如下图所示，可以看出状态变量基本收敛到真实值（由于传感器和模型噪声不可消除，因此只能是对真实状态的最优估计）。
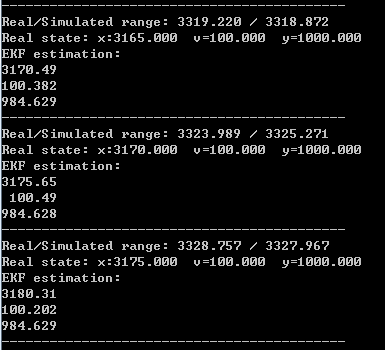
参考：
Eigen: C++开源矩阵计算工具——Eigen的简单用法
KFilter - Free C++ Extended Kalman Filter Library
How to Use this Extended Kalman Filter Library?
http://www.mrpt.org/Kalman_Filters
http://reference.mrpt.org/devel/classmrpt_1_1bayes_1_1_c_kalman_filter_capable.html
https://github.com/MRPT/mrpt/blob/master/samples/bayesianTracking/test.cpp