[CodeForces] 1017C The Phone Number

The Phone Number

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mrs. Smith is trying to contact her husband, John Smith, but she forgot the secret phone number!

The only thing Mrs. Smith remembered was that any permutation of $\mathrm{nn can\; be\; a\; secret\; phone\; number.\; Only\; those\; permutations\; that\; minimize\; secret\; value\; might\; be\; the\; phone\; of\; her\; husband.}$

The sequence of $\mathrm{nn integers\; is\; called\; a\; permutation\; if\; it\; contains\; all\; integers\; from 11 to nn exactly\; once.}$

The secret value of a phone number is defined as the sum of the length of the longest increasing subsequence (LIS) and length of the longest decreasing subsequence (LDS).

A subsequence ${\mathrm{ai1,ai2,\dots ,aikai1,ai2,\dots ,aik where 1\le i1<i2<\dots <ik\le n1\le i1<i2<\dots <ik\le n is\; called\; increasing\; if ai1<ai2<ai3<\dots <aikai1<ai2<ai3<\dots <aik.\; If ai1>ai2>ai3>\dots >aikai1>ai2>ai3>\dots >aik,\; a\; subsequence\; is\; called\; decreasing.\; An\; increasing/decreasing\; subsequence\; is\; called\; longest\; if\; it\; has\; maximum\; length\; among\; all\; increasing/decreasing\; subsequences.}}^{}$

For example, if there is a permutation $[6,4,1,7,2,3,5][6,4,1,7,2,3,5], LIS of\; this\; permutation\; will\; be [1,2,3,5][1,2,3,5],\; so\; the\; length\; of LIS is\; equal\; to 44. LDS can\; be [6,4,1][6,4,1], [6,4,2][6,4,2],\; or [6,4,3][6,4,3],\; so\; the\; length\; of LDS is 33.$

Note, the lengths of LIS and LDS can be different.

So please help Mrs. Smith to find a permutation that gives a minimum sum of lengths of LIS and LDS.

Input

The only line contains one integer $\mathrm{nn (1\le n\le 1051\le n\le 105) —\; the\; length\; of\; permutation\; that\; you\; need\; to\; build.}$

Output

Print a permutation that gives a minimum sum of lengths of LIS and LDS.

If there are multiple answers, print any.

Examples

input

Copy

4

output

Copy

3 4 1 2

input

Copy

2

output

Copy

2 1

Note

In the first sample, you can build a permutation $[3,4,1,2][3,4,1,2]. LIS is [3,4][3,4] (or [1,2][1,2]),\; so\; the\; length\; of LIS is\; equal\; to 22. LDS can\; be\; ony\; of [3,1][3,1], [4,2][4,2], [3,2][3,2],\; or [4,1][4,1].\; The\; length\; of LDS is\; also\; equal\; to 22.\; The\; sum\; is\; equal\; to 44.\; Note\; that [3,4,1,2][3,4,1,2] is not the\; only\; permutation\; that\; is\; valid.$

In the second sample, you can build a permutation $[2,1][2,1]. LIS is [1][1] (or [2][2]),\; so\; the\; length\; of LIS is\; equal\; to 11. LDS is [2,1][2,1],\; so\; the\; length\; of LDS is\; equal\; to 22.\; The\; sum\; is\; equal\; to 33.\; Note\; that\; permutation [1,2][1,2] is\; also\; valid.$

$题目解析$

又是构造题，今天的第三道构造了，香啊，题简单难度评级高特有成就感

网上的什么dilworth我看不懂也不想看

给出一个简单的构造证明，图是个好东西啊

我们用一条y = x的线来描述一个递增的数列，此时最长上升子序列长度是黑色部分全部，

研究一下样例，我们发现样例1是这样的（下面的图），这时候最长上升子序列是黑色部分中最长的一段，而最长下降子序列是绿色部分，因为两条黑线平行，所以两条线间距离相等，最长下降也得出来了。

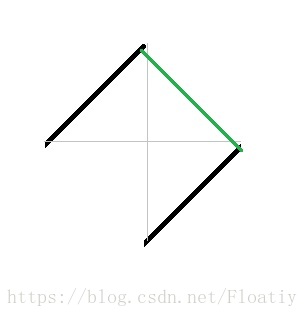
因为黑线间任意两处距离相等，我们可以认为最长下降子序列是连接所有黑线上端点的绿线，那么绿线长度就是黑线的段数了

可以试着进一步推导，发现每段黑色的长度*段数 = 总长。

换言之，最长上升 * 最长下降 = 总长

根据小学知识（因为这四个字今天被同机房的dalao们喷了），当最长上升 = 最长下降 = 根号（总长）时，两者的和最小。

证明毕，写代码吧，注意我对于不能被整开根的部分的处理方法

Code

//by floatiy

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

int n,tot;
int prt;
int main() {
    scanf("%d",&n);
    int siz = ceil(sqrt(n));
    for(int i = 1;i <= siz;i++) {
        for(int j = 1;j <= siz;j++) {
            prt = n - i * siz + j;
            if(prt > 0) printf("%d ",prt);
            tot++;
        }
    }
    for(int i = 1;i <= n - tot;i++) printf("%d ",i);
    return 0;
}