01.组合数
(1)
算法:n!/(n-k)!k!.创建递归算法求N的阶乘。
设计思想:递归
源代码:
//求N!
import javax.swing.*;
public class Ncheng {
public static void main(String args[]) {
String input1=JOptionPane.showInputDialog("enter the number(下标):");
int in1=Integer.parseInt(input1);
String input2=JOptionPane.showInputDialog("enter the number(上标):");
int in2=Integer.parseInt(input2);
int out1=jiecheng(in1);
int out2=jiecheng(in2);
int out3=jiecheng(in1-in2);
int out4=out1/(out2*out3);
JOptionPane.showMessageDialog(null,"N!="+out4,"result:",JOptionPane.CANCEL_OPTION);
}
//递归求阶乘
public static int jiecheng(int n) {
if(n==1)
return 1;
else
return n*jiecheng(n-1);
}
}
结果截图:
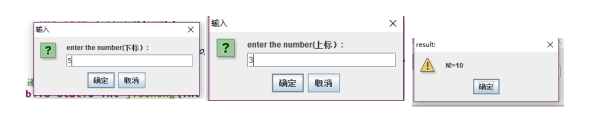
(2)
杨辉三角递推。
设计思想:循环+二维数组=存杨辉三角塔中的数字。
源代码:
//循环+二维数组=组合数
import java.util.Scanner;
public class Ncheng3 {
public static void main(String args[]) {
Scanner scan=new Scanner(System.in);
System.out.print("enter the N:");
int n=scan.nextInt();
System.out.print("enter the K:");
int k=scan.nextInt();
//定义二维数组
int num[][]=new int[(n+1)][];
//利用杨辉三角规律 给二维数组存数
//第一个元素初始化
num[0]=new int[1];
num[0][0]=0;
for(int i=1;i<n+1;i++) {
//实现二维数组
num[i]=new int[i+1];
num[i][0]=1;
for(int j=1;j<i;j++) {
num[i][j]=num[i-1][j-1]+num[i-1][j];
}
num[i][i]=1;
}
System.out.println("在"+n+"中选"+k+"个,有多少种方法:"+num[n][k]);
}
}
结果截图:
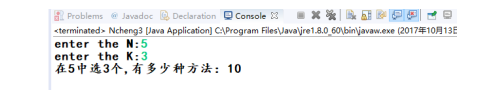
(3)
用递归实现杨辉三角
设计思想:自己调用自己,有调用出口。
源代码:
//递推实现组合数
import java.util.Scanner;
public class Ncheng2 {
public static void main(String args[]) {
int n,k,tem;
System.out.print("从n个中选k个,n=");
Scanner scan=new Scanner(System.in);
n=scan.nextInt();
System.out.print("从n个中选k个,k=");
k=scan.nextInt();
tem=numOf(n,k);
System.out.println("在"+n+"中选"+k+"个,有多少种方法:"+tem);
}
public static int numOf(int n,int k) {
int x;
if(n==k)
return 1;
else if(k==1)
return n;
else
x=numOf(n-1,k)+numOf(n-1,k-1);
return x;
}
}
结果截图:
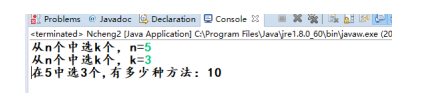
02.汉诺塔-递归
设计思想:
(1)将n上n-1层放到B柱上
(2)将第N层放到C柱上
(3)再将n-1层放到C柱上
(4)递归调用直到N=1.
程序流程图:

原代码:
import java.util.Scanner;
public class Hanoi {
@SuppressWarnings("resource")
public static void main(String args[]) {
System.out.print("enter the number of tower:");
Scanner scan=new Scanner(System.in);
int in=scan.nextInt();
System.out.println("Handle:");
handle(in,'A','B','C');
}
//每一步的移动
//将第n层从A移动到B;
static void move(int n,char A,char B) {
System.out.println("第"+n+"个"+A+"->"+B);
}
//递归处理汉诺塔
//将n层从A借助B移动到C;
static void handle(int n,char A,char B,char C) {
if(n==1)
move(1,A,C);
else {
handle(n-1,A,C,B);
move(n,A,C);
handle(n-1,B,A,C);
}
}
}
结果截图:

03.回文
设计思想:
(1)判断第一个字符和倒数第一个字符是否相同
(2)是,再判断第二个字符和倒数第二个字符是否相同
(3)依次判断直到判断中间的字符(判断出口)
程序流程图:

源代码:
import java.util.Scanner;
//回文
//递归
public class Palindrome {
public static void main(String args[]) {
System.out.println("enter a string:");
Scanner scan=new Scanner(System.in);
String str=scan.next();
if(handle(str,0,str.length()-1)==1) {
System.out.println("句子是回文!");
}
else
System.out.println("句子不是回文!");
}
//判断
public static int handle(String ss,int i,int j) {
int x=0;
if(i==j||(i+1)==j)
x=1;
else {
if(ss.charAt(i++)==ss.charAt(j--))
x=handle(ss,i,j);
}
return x;
}
}
结果截图:
