题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
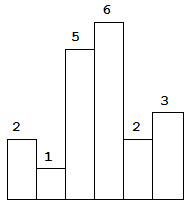
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
题目链接: https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
思路1
保留求解。使用两层循环,外层循环为 i,内层循环为 j,j>=i,计算 [i, j] 范围内的最大面积。代码如下:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
if(heights.empty()) return 0;
int maxArea = -1;
for(int i=0; i<heights.size(); i++){
int minHeight = INT_MAX; // [i, j]范围内柱子的最低高度
for(int j = i; j<heights.size(); j++){
minHeight = min(heights[j], minHeight);
maxArea = max(minHeight*(j-i+1), maxArea);
}
}
return maxArea;
}
};
// 超时
该方法超时未通过。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
思路2
遍历数组,当遍历到 i 时,从 i 开始向两边寻找不小于 height[i] 的元素,然后求面积即可,记录最大的面积作为答案。代码如下:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
if(heights.empty()) return 0;
int maxArea = -1;
for(int i=0; i<heights.size(); i++){
int curHeight = heights[i];
int left = i, right = i;
while(left>=0 && heights[left]>=curHeight) left--;
while(right<heights.size() && heights[right]>=curHeight) right++;
maxArea = max(curHeight*(right-left-1), maxArea); // (right-1)-(left+1)+1=right-left-1
}
return maxArea;
}
};
// 超时
虽然这种方法会超时,但是我们可以在这个思路的基础上进行优化,得到思路3.
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
思路3
思路 2 超时的原因是遍历到每个元素都要向两边扩散求矩形宽度,我们可以使用单调栈来加快求宽度的过程。
单调栈分为单调递增栈和单调递减栈。单调递增栈从栈底到栈顶的元素是递增的,单调递减栈则相反。这里我们使用的是单调递增栈。
单调递增栈插入元素的方法如下:
- 如果新元素大于栈顶元素,则直接放进栈顶;
- 如果新元素小于栈顶元素,则弹出栈顶元素,直到栈顶元素小于新元素,然后将新元素放进栈顶。
使用代码描述如下:
stack<int> st;
for(int i = 0; i < nums.size(); i++)
{
while(!st.empty() && st.top() > nums[i])
{
st.pop();
}
st.push(nums[i]);
}
根据单调递增栈插入元素的特点,单调递增栈满足以下3个性质:
- 栈中元素递增;
- 当元素出栈后,新元素是从出栈元素位置向后数第一个小于出栈元素的元素:例如,数组为 [2,1,5,6,2,3],假设栈中的元素为 [1,5,6],新元素为 2,因为 2<6,则 6 要出栈,而 2 是从 6 往后数第一个小于 6 的元素;
- 当元素出栈后,新的栈顶元素是出栈元素往左数第一个小于出栈元素的元素:与上面一样的例子,假设栈中的元素为 [1,5,6],新元素为 2,此时 6 出栈,则新的栈顶元素为 5,5 是 6 左边第一个小于 6 的元素。
通过后两个性质,我们就能快速地知道当前元素的左右边界,从而避免了思路 2 当中向左右遍历的方式。代码如下:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
if(heights.empty()) return 0;
int maxArea = -1;
stack<int> s;
heights.push_back(0);
for(int i=0; i<heights.size(); i++){
while(!s.empty() && heights[s.top()]>=heights[i]){
int curHeight = heights[s.top()]; s.pop();
if(s.empty()){
maxArea = max(i*curHeight, maxArea);
}else{
maxArea = max((i-s.top()-1)*curHeight, maxArea);
}
}
s.push(i);
}
return maxArea;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)