1.什么是树形动态规划???


是不是看不懂?
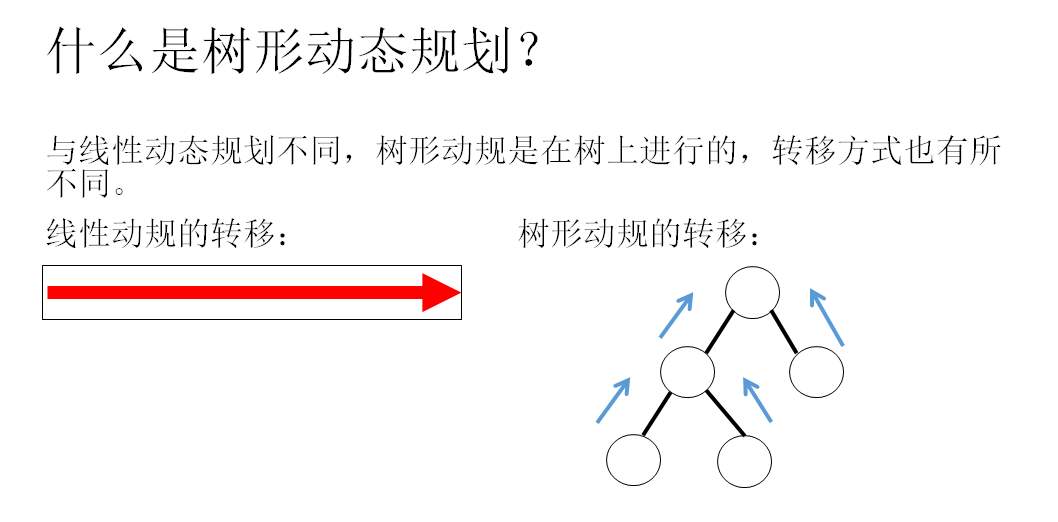
这样好点了吧。
常规就是开个二维数组或者结构图或者balablala
记载左右儿子的信息。
来看一道伪树形dp...
P1040 加分二叉树
设一个n个节点的二叉树tree的中序遍历为(1,2,3,…,n),其中数字1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第i个节点的分数为di,tree及它的每个子树都有一个加分,
任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分× subtree的右子树的加分+subtree的根的分数。
若某个子树为空,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出;
(1)tree的最高加分
(2)tree的前序遍历
输入输出格式
输入格式:
第1行:1个整数n(n<30),为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(分数<100)。
输出格式:
第1行:1个整数,为最高加分(Ans ≤4,000,000,000)。
第2行:n个用空格隔开的整数,为该树的前序遍历。
输入输出样例
题意:构造一个最优解的树。这是一个线性dp。所以并不是树形dp..
由于中序遍历下,编号 < i 的是 i 的左子树,右子树反之。
所以我们三层for
1 for(int i=n;i>=1;i--) 2 for(int j=i+1;j<=n;j++) 3 for(int k=i;k<=j;k++)
做什么呢?
逐一计算答案。判断哪个是根。转移方程很熟悉。
if(f[i][j]<f[i][k-1]*f[k+1][j]+f[k][k])
f[i][j]=f[i][k-1]*f[k+1][j]+f[k][k],rt[i][j]=k;
因为还要我们输出先序遍历,所以记下root。
这是一道伪树形的水题,直接给代码辽
1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 int n,f[40][40],rt[40][40]; 5 inline void print(int l,int r){ 6 if(l>r)return ; 7 if(l==r){printf("%d ",l);return ;} 8 printf("%d ",rt[l][r]); 9 print(l,rt[l][r]-1); 10 print(rt[l][r]+1,r); 11 } 12 int main(){ 13 cin>>n; 14 for(int i=1;i<=n;i++)cin>>f[i][i],f[i][i-1]=1; 15 for(int i=n;i>=1;i--) 16 for(int j=i+1;j<=n;j++) 17 for(int k=i;k<=j;k++) 18 if(f[i][j]<f[i][k-1]*f[k+1][j]+f[k][k]) 19 f[i][j]=f[i][k-1]*f[k+1][j]+f[k][k],rt[i][j]=k; 20 printf("%d ",f[1][n]); 21 print(1,n); 22 return 0; 23 }
emmm再看二叉苹果树之前,我们先看一道与之类似的。

想一想怎么表示状态??

既然有实现1,那当然有实现2,而且貌似更容易学……
但是为什么要放上来?
因为状态转移方程是类似的。
因为很多细节在这张图片里面。
“f[i][j]表示以第i个节点为根的子树保留j个节点的xxxxx。”很常用,比如等等下面的二叉苹果树。
放一下实现1.

实现2:

别急。看代码之前说明一个问题,这只是部分代码(ppt也没给我全部代码啊。。),看不懂没有关系
笔者建议从下面的二叉苹果树开始看,代码完整,也有题解及我的注释。二叉苹果树我用的是动态数组,这边用的是结构体存边点
然后可以再回头看
把这题提上来讲是因为题目简单明了,两种实现方法的讲解也很适合初学者。至于这实现2也有几种实现方法,比如下一题我就是用了vector。
1 int dfs(int x,int fa){ 2 int d=0;//d为该节点的子树的边数 3 for(int i=h[x];i;i=e[i].nx){ 4 int v=e[i].to,w=e[i].w; 5 if(v==fa)continue ; 6 d+=dfs(v,x)+1;//looook "+1" !!! 7 for(int j=min(d,m);j>=1;j--) 8 for(int k=min(d,j);k>=1;k--) 9 f[x][j]=max(f[x][j],f[x][j-k]+f[v][k-1]+w); 10 //k-1是因为还有儿子自己 w就是儿子自己 这对应实现2的ppt截图会很清楚 11 } 12 return d; 13 }
P2015 二叉苹果树
题目描述
有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有1个儿子的结点)
这棵树共有N个结点(叶子点或者树枝分叉点),编号为1-N,树根编号一定是1。
我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝的树
2 5
/
3 4
/
1现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
输入输出格式
输入格式:
第1行2个数,N和Q(1<=Q<= N,1<N<=100)。
N表示树的结点数,Q表示要保留的树枝数量。接下来N-1行描述树枝的信息。
每行3个整数,前两个是它连接的结点的编号。第3个数是这根树枝上苹果的数量。
每根树枝上的苹果不超过30000个。
输出格式:
一个数,最多能留住的苹果的数量。
输入输出样例
21


1 #include <iostream> 2 #include <cstdio> 3 #include <vector> 4 #include <algorithm> 5 #include <cstring> 6 #define ll long long 7 #define fo(i,j,k) for(int i=j;i<=k;i++) 8 using namespace std; 9 vector <int> f[105],w[105]; 10 int n,m; 11 int dp[105][105]; 12 inline void dfs(int u,int fa){//当前点,上一个点 13 for(int i=0;i<f[u].size();i++){ 14 int v=f[u][i],t=w[u][i];//找到和当前点由树枝相连的点 15 if(v==fa)continue ;//不拔起上一个点是吧 16 dfs(v,u);//深搜-- 17 // f[i][j]表示以第i个节点为根的子树保留j个节点的最大权和。 18 for(int j=m;j;j--) 19 fo(k,0,j-1) 20 dp[u][j]=max(dp[u][j],dp[u][k]+dp[v][j-k-1]+t);//保留j个,或者k个 21 //那么对于左子树保留了k个,右子树保留了j-k-1个(因为当前节点保留,所以-1) 22 //保留?取决于谁留下的苹果多。当然加上当前节点苹果树t 23 } 24 } 25 int main(){ 26 int u,v,d; 27 scanf("%d%d",&n,&m); 28 fo(i,2,n){ 29 scanf("%d%d%d",&u,&v,&d); 30 f[u].push_back(v);f[v].push_back(u); 31 w[u].push_back(d);w[v].push_back(d); 32 } 33 dfs(1,0); 34 printf("%d ",dp[1][m]); 35 return 0; 36 }
例子2:
有一棵树,n个节点,规定选了一个点,它相邻的点就不能选。问最多能选多少个点,并判断是否有唯一解?
n<=300。
实现:


第二个问题:多叉树转二叉树
拿一题 选课。
P2014 选课
题目描述
在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习,在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习。现在有N门功课,每门课有个学分,每门课有一门或没有直接先修课(若课程a是课程b的先修课即只有学完了课程a,才能学习课程b)。一个学生要从这些课程里选择M门课程学习,问他能获得的最大学分是多少?
输入输出格式
输入格式:
第一行有两个整数N,M用空格隔开。(1<=N<=300,1<=M<=300)
接下来的N行,第I+1行包含两个整数ki和si, ki表示第I门课的直接先修课,si表示第I门课的学分。若ki=0表示没有直接先修课(1<=ki<=N, 1<=si<=20)。
输出格式:
只有一行,选M门课程的最大得分。
输入输出样例
7 4 2 2 0 1 0 4 2 1 7 1 7 6 2 2
13
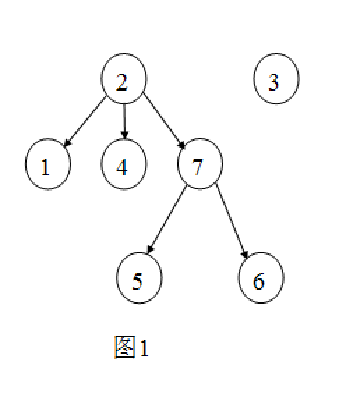
 图就这样....
图就这样....

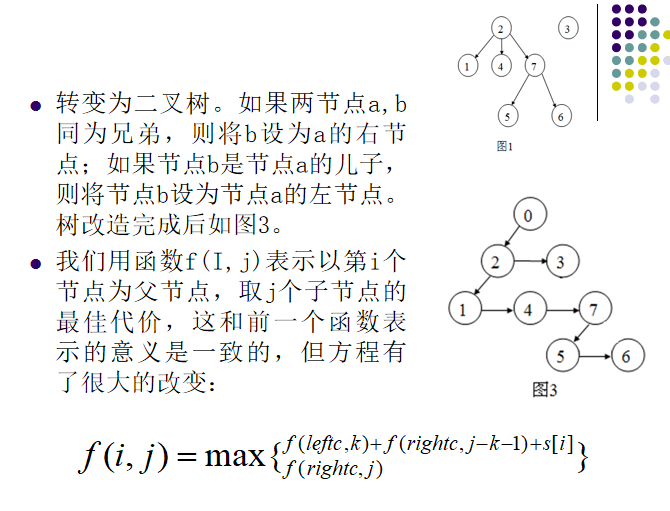

多叉树转二叉树后就可以轻松解决了。
定义f[i][j]为i的所有兄弟和i的所有儿子,和i自己,学j门课的最大学分总和。
不学i这门课,全部学兄弟的课程:
f[i][j]=max(f[i][j],f[rson][j])
学i及i的先修课:
f[i][j]=max(f[i][j],f[rson][j-k-1],f[lson][k]+w[i])


emmmm原本按照上面的方法码了一遍莫名其妙bug了
于是一气之下码了背包。
当然是看了9021.
1 #include <iostream> 2 using namespace std; 3 int g[302][302],f[302][302],v[302],m,n,x,y; 4 inline int dfs(int s){ 5 int ans=0; 6 for(int i=1;i<=m;i++){ 7 if(g[s][i]){ 8 ans+=dfs(i)+1; 9 for(int j=min(ans,m);j;j--) 10 for(int k=0;k<j;k++) 11 f[s][j]=max(f[s][j],f[s][k]+f[i][j-k-1]+v[i]); 12 } 13 } 14 return ans; 15 } 16 int main(){ 17 cin>>m>>n; 18 for(int i=1;i<=m;i++){ 19 cin>>x>>y; 20 g[x][i]=1,v[i]=y; 21 } 22 dfs(0); 23 cout<<f[0][n]<<endl; 24 }
ans只是要选的课程数 不是总学分。。

皇宫看守(Vijos 1144 小胖守皇宫)
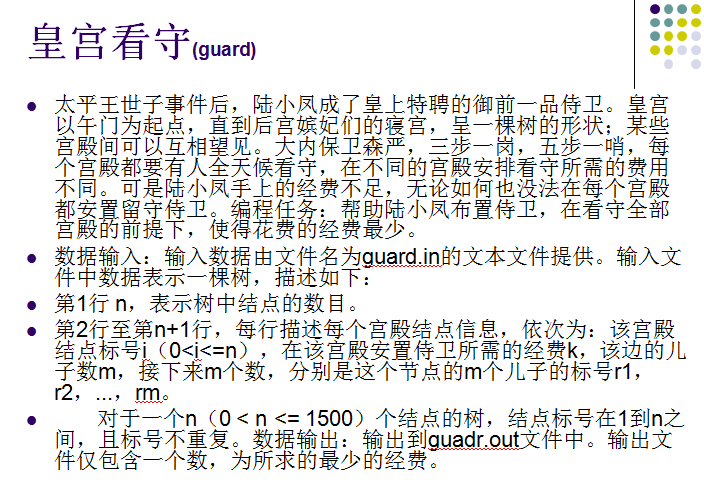
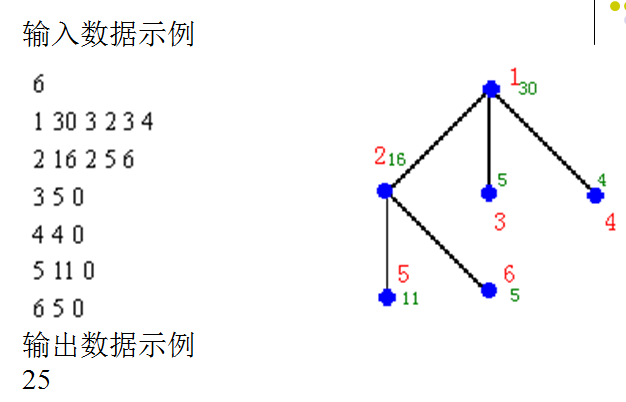
题目思路:
【树形DP】
F[X][0]表示结点X的父亲放了守卫的最小花费,
F[X][1]表示结点X自身放了守卫的最小花费,
F[X][2]表示结点X和父亲都不放守卫,X的其中一个儿子放了守卫的最小花费。
这样,父亲放了守卫,X可以选择放守卫(F[X][1]),或者可以是 儿子放或不放守卫(F[son][1],F[son][2])
自身放守卫,则儿子都是父亲放了守卫(F[son][0])
其中一个儿子放了守卫,则枚举哪个儿子是最优值。(F[son][1],F[son][0])
这样最终可以推出转移方程。
原文:https://blog.csdn.net/u010568270/article/details/65444860
改动后代码(其实只是改了码风和一些不必要的东西):
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #define MAX 0x7fffffff 5 #define N 1504 6 #define R register 7 using namespace std; 8 int n,m,f[N][3]; 9 bool u[N]; 10 struct xxx{ 11 int num,c;//儿子数,安置花费 12 int s[N];//儿子编号 13 }a[N]; 14 inline int ri(){ 15 char c=getchar();int x=0,w=1; 16 while(!isdigit(c)){if(c=='-')w=-1;c=getchar();} 17 while( isdigit(c)){x=(x<<3)+(x<<1)+c-48;c=getchar();} 18 return x*w; 19 } 20 inline void dp(int now){ 21 if(u[now])return; 22 if(!a[now].num){//根 23 f[now][1] = f[now][2] = a[now].c , f[now][0] = 0; 24 return ; 25 } 26 for(int i=1;i<=a[now].num;i++) 27 dp(a[now].s[i]);//搜索每一个儿子 28 f[now][0]=0; 29 30 for(int j=1;j<=a[now].num;j++) 31 f[now][0]+=min(f[a[now].s[j]][1],f[a[now].s[j]][2]);//已经放了守卫,儿子可放可不放 32 f[now][2]=MAX; 33 34 for(int j=1;j<=a[now].num;j++)//不放守卫,则儿子放,孙子可放可不放 35 f[now][2]=min(f[now][2],f[now][0]-min(f[a[now].s[j]][1],f[a[now].s[j]][2])+f[a[now].s[j]][1]); 36 f[now][1]=a[now].c; 37 38 for(int j=1;j<=a[now].num;j++) 39 f[now][1]+=f[a[now].s[j]][0];//自身放守卫,则儿子都是父亲放了守卫(F[son][0]) 40 f[now][0]=min(f[now][0],f[now][1]); 41 } 42 int main(){ 43 int x,y,z; 44 while(scanf("%d",&n)){ 45 for(int i=1;i<=n;i++){ 46 x=ri(), a[x].c=ri(), a[x].num=ri(); 47 for(int j=1;j<=a[x].num;j++) 48 a[x].s[j]=ri(),u[a[x].s[j]]=1;//记录该节点 49 } 50 for(m=1;m<=n;m++) if(!u[m]) break;//找节点最小的 51 memset(u,0,sizeof(u)); 52 dp(m); 53 printf("%d ",min(f[m][1],f[m][2])); 54 } 55 return 0; 56 }
(也不知道有没有错)
...