#include<stdio.h>
#define MAXNUM 100
typedef int KeyType;
typedef int DataType;
typedef struct {
KeyType key; /* 排序码字段 */
/*DataType info; 记录的其它字段 */
} RecordNode;
typedef struct {
int n; /* n为文件中的记录个数,n<MAXNUM */
RecordNode record[MAXNUM];
} SortObject;
void binSort(SortObject * pvector) { /* 按递增序进行二分法插入排序 */
int i, j, left, mid, right;
RecordNode temp;
RecordNode *data = pvector->record;
for( i = 1; i < pvector->n; i++ ) {
temp = data[i];
left = 0; right = i-1; /* 置已排序区间的下、上界初值 */
while (left <= right) {
mid = (left + right)/2; /* mid指向已排序区间的中间位置 */
if (temp.key < data[mid].key)
right = mid-1; /* 插入元素应在左子区间 */
else left = mid+1; /* 插入元素应在右子区间 */
}
for (j = i-1; j >= left; j--)
data[j+1] = data[j]; /* 将排序码大于ki的记录后移 */
if (left != i) data[left] = temp;
}
}
SortObject vector={10, 49,38,65,97,76,13,27,49,50,101};
int main(){
int i;
binSort(&vector);
for(i = 0; i < vector.n; i++)
printf("%d ", vector.record[i]);
getchar();
return 0;
}
修改代码如下:
/* 二分法插入排序的算法源程序*/
#include<stdio.h>
#include<iostream.h>
#include<iomanip.h>
#include<stdlib.h>
#include<time.h>
#include<malloc.h>
#define MAXNUM 100
#define MAXI 10;
typedef int KeyType;
typedef int DataType;
typedef struct {
KeyType key; /* 排序码字段 */
/*DataType info; 记录的其它字段 */
} RecordNode;
typedef struct {
int n; /* n为文件中的记录个数,n<MAXNUM */
RecordNode record[MAXNUM];
} SortObject;
void binSort(SortObject * pvector) { /* 按递增序进行二分法插入排序 */
int i, j, left, mid, right;
RecordNode temp;
RecordNode *data = pvector->record;
for( i = 1; i < pvector->n; i++ ) {
temp = data[i];
left = 0; right = i-1; /* 置已排序区间的下、上界初值 */
while (left <= right) {
mid = (left + right)/2; /* mid指向已排序区间的中间位置 */
if (temp.key < data[mid].key)
right = mid-1; /* 插入元素应在左子区间 */
else left = mid+1; /* 插入元素应在右子区间 */
}
for (j = i-1; j >= left; j--)
data[j+1] = data[j]; /* 将排序码大于ki的记录后移 */
if (left != i) data[left] = temp;
}
}
//SortObject vector={10, 49,38,65,97,76,13,27,49,50,101};
int main(){
int i;
SortObject vector;
vector.n=MAXI;
//vector.record= new record[MAXNUM]; //再次在这个地方碰到问题,vector.record= new vector.record= RecordNode[MAXNUM]; 事实上,在这//里,问题更加容易处理,就是直接定义vector,然后,对n初始化即可
for( i=1;i<vector.n;i++)
srand(time(0));
{//a.record[i] = (pu)malloc( sizeof(RecordNode));
vector.record[i].key=rand()%80;
//a.record[i].data=rand()%100;
}
binSort(&vector);
for(i = 0; i < vector.n; i++)
printf("%d ", vector.record[i]);
getchar();
return 0;
}
经过测试运行后的完整代码:
/* 二分法插入排序的算法源程序*/
#include<stdio.h>
#include<iostream.h>
#include<iomanip.h>
#include<stdlib.h>
#include<time.h>
#include<malloc.h>
#define MAXNUM 100
#define MAXI 10;
typedef int KeyType;
typedef int DataType;
typedef struct {
KeyType key; /* 排序码字段 */
/*DataType info; 记录的其它字段 */
} RecordNode;
typedef struct {
int n; /* n为文件中的记录个数,n<MAXNUM */
RecordNode record[MAXNUM];//相当于typedef RecordNode record[MAXNUM];
} SortObject;
void binSort(SortObject * pvector ,int n) { /* 按递增序进行二分法插入排序 */
int i, j, left, mid, right;
RecordNode temp;
RecordNode *data = pvector->record;
for( i = 1; i < pvector->n; i++ ) {
temp = data[i];
left = 0; right = i-1; /* 置已排序区间的下、上界初值 */
while (left <= right) {
mid = (left + right)/2; /* mid指向已排序区间的中间位置 */
if (temp.key < data[mid].key)
right = mid-1; /* 插入元素应在左子区间 */
else left = mid+1; /* 插入元素应在右子区间 */
}
for (j = i-1; j >= left; j--)
data[j+1] = data[j]; /* 将排序码大于ki的记录后移 */
if (left != i) data[left] = temp;
for(int k=0;k<n;k++)
cout<<setw(4)<<pvector->record[k].key;
cout<<endl;
}
}
//SortObject vector={10, 49,38,65,97,76,13,27,49,50,101};
int main(){
int i;
SortObject vector;
vector.n=MAXI;
//vector.record = new RecordNode ;
srand(time(0));
for( i=0;i<vector.n;i++)
{
//a.record[i] = (pu)malloc( sizeof(RecordNode));
vector.record[i].key=rand()%80;
//a.record[i].data=rand()%100;
}
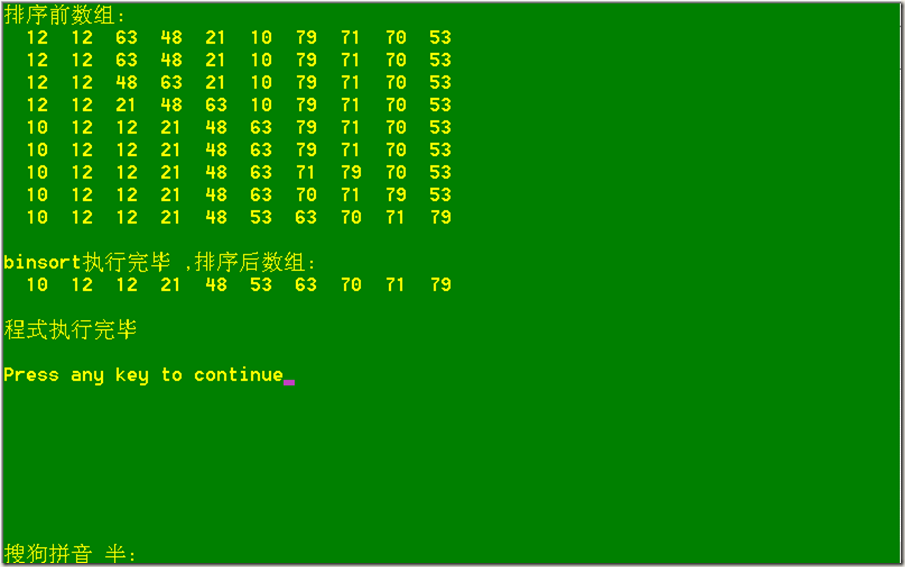
cout<<"排序前数组:\n";
binSort(&vector,vector.n);
cout<<"\nbinsort执行完毕 ,排序后数组:\n";
for(i = 0; i < vector.n; i++)
cout<<setw(4)<<vector.record[i].key;
cout<<endl;
cout<<"\n程式执行完毕\n"<<endl;
//getchar();
return 0;
}
binSort(SortObject * pvector ,int n)算法的深入分析如下:
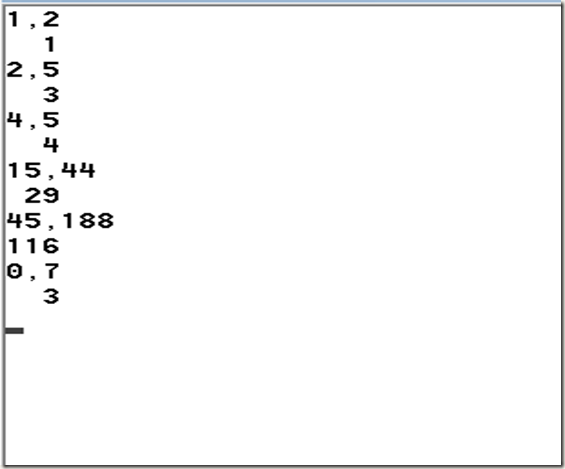
关于mid = (left + right)/2; 对于除不整的情况,进行模拟,
代码如下:
#include "stdio.h"
#define MAXI 10
void main()
{
int right;
int left;
int mid;
int i;
for( i=0;i<MAXI;i++)
{scanf("%3d,%3d",&right,&left);//注意用逗号隔开,在输入时
mid=(right+left)/2;
printf("%3d\n",mid);
}
}
证实情况是 取整数,这个无所谓,反正,就是划分区域,具体是那个那个不重要,重要的是,所以要分析的对象均没有遗漏,显然这点满足