转载自:https://www.cnblogs.com/biyeymyhjob/archive/2012/07/17/2595249.html
概念
TF-IDF(term frequency–inverse document frequency)是一种用于资讯检索与资讯探勘的常用加权技术。
TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
TF-IDF加权的各种形式常被搜寻引擎应用,作为文件与用户查询之间相关程度的度量或评级。除了TF-IDF以外,因特网上的搜寻引擎还会使用基于连结分析的评级方法,以确定文件在搜寻结果中出现的顺序。
Tf-idf
用途:关键词提取
IDF:Inverse Document Frequency,逆文档频率
$ TF = frac{ 某词在某文章中出现的次数 }{ 文章的总词数 } $
$ IDF = log{frac{ 语料库的文档总数 }{ 包含该词的文档数 + 1} } $
$ TF-IDF = TF * IDF $
示例:
《中国的蜜蜂养殖》: 进行词频(Term Frequency,缩写为TF)统计
出现次数最多的词是----“的”、“是”、“在”----这一类最常用的词(停用词)
“中国”、“蜜蜂”、“养殖”这三个词的出现次数一样多,重要性是一样的?
"中国"是很常见的词,相对而言,"蜜蜂"和"养殖"不那么常见
《中国的蜜蜂养殖》:假定该文长度为1000个词,"中国"、"蜜蜂"、"养殖"各出现20次, 则这三个词的"词频"(TF)都为0.02;
搜索Google发现,包含"的"字的网页共有250亿张,假定这就是中文网页总数。 包含"中国"的网页共有62.3亿张,包含"蜜蜂"的网页为0.484亿张, 包含"养殖"的网页为0.973亿张
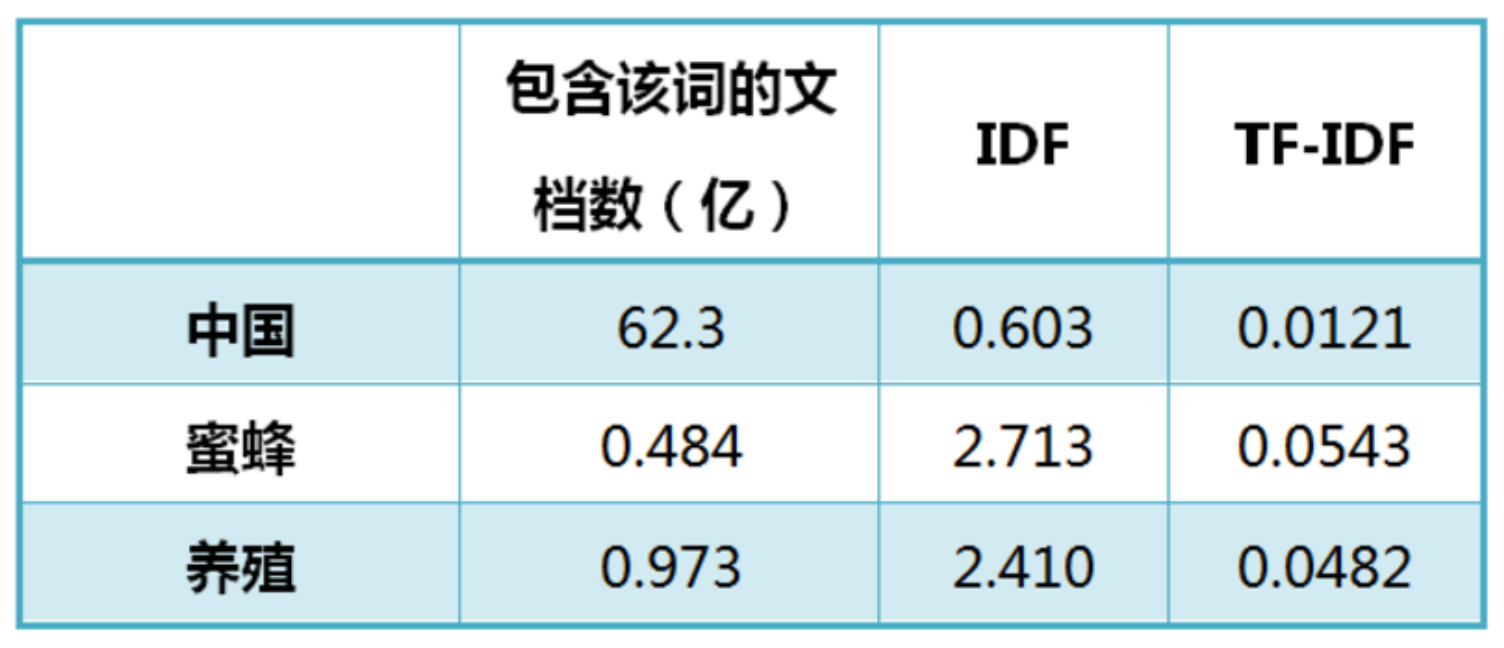
原理
在一份给定的文件里,词频 (term frequency, TF) 指的是某一个给定的词语在该文件中出现的次数。这个数字通常会被归一化(分子一般小于分母 区别于IDF),以防止它偏向长的文件。
(同一个词语在长文件里可能会比短文件有更高的词频,而不管该词语重要与否。)
逆向文件频率 (inverse document frequency, IDF) 是一个词语普遍重要性的度量。某一特定词语的IDF,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取对数得到。
某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语。
TFIDF的主要思想是:如果某个词或短语在一篇文章中出现的频率TF高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TFIDF实际上是:TF * IDF,
TF词频(Term Frequency),IDF反文档频率(Inverse Document Frequency)。
TF表示词条在文档d中出现的频率(另一说:TF词频(Term Frequency)指的是某一个给定的词语在该文件中出现的次数)。
IDF的主要思想是:如果包含词条t的文档越少,也就是n越小,IDF越大,则说明词条t具有很好的类别区分能力。
如果某一类文档C中包含词条t的文档数为m,而其它类包含t的文档总数为k,显然所有包含t的文档数n=m+k,当m大的时候,n也大,按照IDF公式得到的IDF的值会小,就说明该词条t类别区分能力不强。
(另一说:IDF反文档频率(Inverse Document Frequency)是指果包含词条的文档越少,IDF越大,则说明词条具有很好的类别区分能力。)
但是实际上,如果一个词条在一个类的文档中频繁出现,则说明该词条能够很好代表这个类的文本的特征,这样的词条应该给它们赋予较高的权重,并选来作为该类文本的特征词以区别与其它类文档。这就是IDF的不足之处.
在一份给定的文件里,词频(term frequency,TF)指的是某一个给定的词语在该文件中出现的频率。这个数字是对词数(term count)的归一化,以防止它偏向长的文件。(同一个词语在长文件里可能会比短文件有更高的词数,而不管该词语重要与否。)对于在某一特定文件里的词语 t_{i} 来说,它的重要性可表示为:
$ mathrm{tf_{i,j}} = frac{n_{i,j}}{sum_k n_{k,j}} $
以上式子中 n_{i,j} 是该词在文件d_{j}中的出现次数,而分母则是在文件d_{j}中所有字词的出现次数之和。
逆向文件频率(inverse document frequency,IDF)是一个词语普遍重要性的度量。某一特定词语的IDF,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取对数得到:
$ mathrm{idf_{i}} = log frac{|D|}{|{j: t_{i} in d_{j}}|} $
其中
|D|:语料库中的文件总数
$ |{ j: t_{i} in d_{j}}| $ :包含词语 t_{i} 的文件数目(即 n_{i,j}
eq 0的文件数目)如果该词语不在语料库中,就会导致被除数为零,因此一般情况下使用1 + |{j : t_{i} in d_{j}}|
然后
$ mathrm{tf{}idf_{i,j}} = mathrm{tf_{i,j}} imes mathrm{idf_{i}} $
某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语。
示例
一:有很多不同的数学公式可以用来计算TF-IDF。这边的例子以上述的数学公式来计算。
词频 (TF) 是一词语出现的次数除以该文件的总词语数。
假如一篇文件的总词语数是100个,而词语“母牛”出现了3次,那么“母牛”一词在该文件中的词频就是3/100=0.03。
一个计算文件频率 (DF) 的方法是测定有多少份文件出现过“母牛”一词,然后除以文件集里包含的文件总数。
所以,如果“母牛”一词在1,000份文件出现过,而文件总数是10,000,000份的话,其逆向文件频率就是 log(10,000,000 / 1,000)=4。最后的TF-IDF的分数为0.03 * 4=0.12。
二:根据关键字k1,k2,k3进行搜索结果的相关性就变成 TF1*IDF1 + TF2*IDF2 + TF3*IDF3。
比如document1的term总量为1000,k1,k2,k3在document1出现的次数是100,200,50。包含了 k1, k2, k3的docuement总量分别是 1000, 10000,5000。document set的总量为10000。
TF1 = 100/1000 = 0.1 TF2 = 200/1000 = 0.2 TF3 = 50/1000 = 0.05 IDF1 = log(10000/1000) = log(10) = 2.3 IDF2 = log(10000/100000) = log(1) = 0; IDF3 = log(10000/5000) = log(2) = 0.69 这样关键字k1,k2,k3与docuement1的相关性= 0.12.3 + 0.20 + 0.05*0.69 = 0.2645 其中k1比k3的比重在document1要大,k2的比重是0.
三:在某个一共有一千词的网页中“原子能”、“的”和“应用”分别出现了 2 次、35 次 和 5 次,那么它们的词频就分别是 0.002、0.035 和 0.005。
我们将这三个数相加,其和 0.042 就是相应网页和查询“原子能的应用” 相关性的一个简单的度量。
概括地讲,如果一个查询包含关键词 w1,w2,...,wN, 它们在一篇特定网页中的词频分别是: TF1, TF2, ..., TFN。 (TF: term frequency)。 那么,这个查询和该网页的相关性就是:TF1 + TF2 + ... + TFN。
读者可能已经发现了又一个漏洞。在上面的例子中,词“的”站了总词频的 80% 以上,而它对确定网页的主题几乎没有用。我们称这种词叫 应删除词(Stopwords),也就是说在度量相关性是不应考虑它们的频率。
在汉语中,应删除词还有“是”、“和”、“中”、“地”、“得”等等几十个。忽略这些应删除词后,上述网页的相似度就变成了0.007,其中“原子能”贡献了 0.002,“应用”贡献了 0.005。
细心的读者可能还会发现另一个小的漏洞。在汉语中,“应用”是个很通用的词,而“原子能”是个很专业的词,后者在相关性排名中比前者重要。因此我们需要给汉语中的每一个词给一个权重,这个权重的设定必须满足下面两个条件:
-
一个词预测主题能力越强,权重就越大,反之,权重就越小。我们在网页中看到“原子能”这个词,或多或少地能了解网页的主题。我们看到“应用”一次,对主题基本上还是一无所知。因此,“原子能“的权重就应该比应用大。
-
应删除词的权重应该是零。
我们很容易发现,如果一个关键词只在很少的网页中出现,我们通过它就容易锁定搜索目标,它的权重也就应该大。
反之如果一个词在大量网页中出现,我们看到它仍然不很清楚要找什么内容,因此它应该小。概括地讲,假定一个关键词 w 在 Dw 个网页中出现过,那么 Dw 越大,w的权重越小,反之亦然。在信息检索中,使用最多的权重是“逆文本频率指数” (Inverse document frequency 缩写为 IDF ),它的公式为 log(D/Dw) 其中D是全部网页数。
比如,我们假定中文网页数是D=10亿,应删除词“的”在所有的网页中都出现,即Dw=10亿,那么它的IDF=log(10亿/10亿)= log (1) = 0。
假如专用词“原子能”在两百万个网页中出现,即Dw=200万,则它的权重IDF=log(500) =6.2。又假定通用词“应用”,出现在五亿个网页中,它的权重IDF = log(2)则只有 0.7。
也就只说,在网页中找到一个“原子能”的比配相当于找到九个“应用”的匹配。利用 IDF,上述相关性计算个公式就由词频的简单求和变成了加权求和,即 TF1IDF1 + TF2IDF2 +... + TFN*IDFN。在上面的例子中,该网页和“原子能的应用”的相关性为 0.0161,其中“原子能”贡献了 0.0126,而“应用”只贡献了0.0035。这个比例和我们的直觉比较一致了。