拉索回归（LASSO Regularizarion）

目录

• 什么是拉索回归
• 比较 Ridge & LASSO
  • L0 正则
  • 弹性网 Elastoc Net
• 代码实现

---

什么是拉索回归

LASSO: Least Absolute Shrinkage and Selection Operator Regression

岭回归的目标：
使 $J( heta) = MSE(Y, hat{y}; heta) alpha frac{1}{2} sum_{i=1}^n heta^2_i $ 尽可能小

LASSO 回归的目标：
使 $J( heta) = MSE(Y, hat{y}; heta) alpha sum_{i=1}^n | heta_i | $ 尽可能小

LASSO趋向于使得一部分theta值变为0。 所以可作为特征选择用（也是名字中 Selection 的意义）。

---

比较 Ridge & LASSO

下面几组式子 模式比较相像

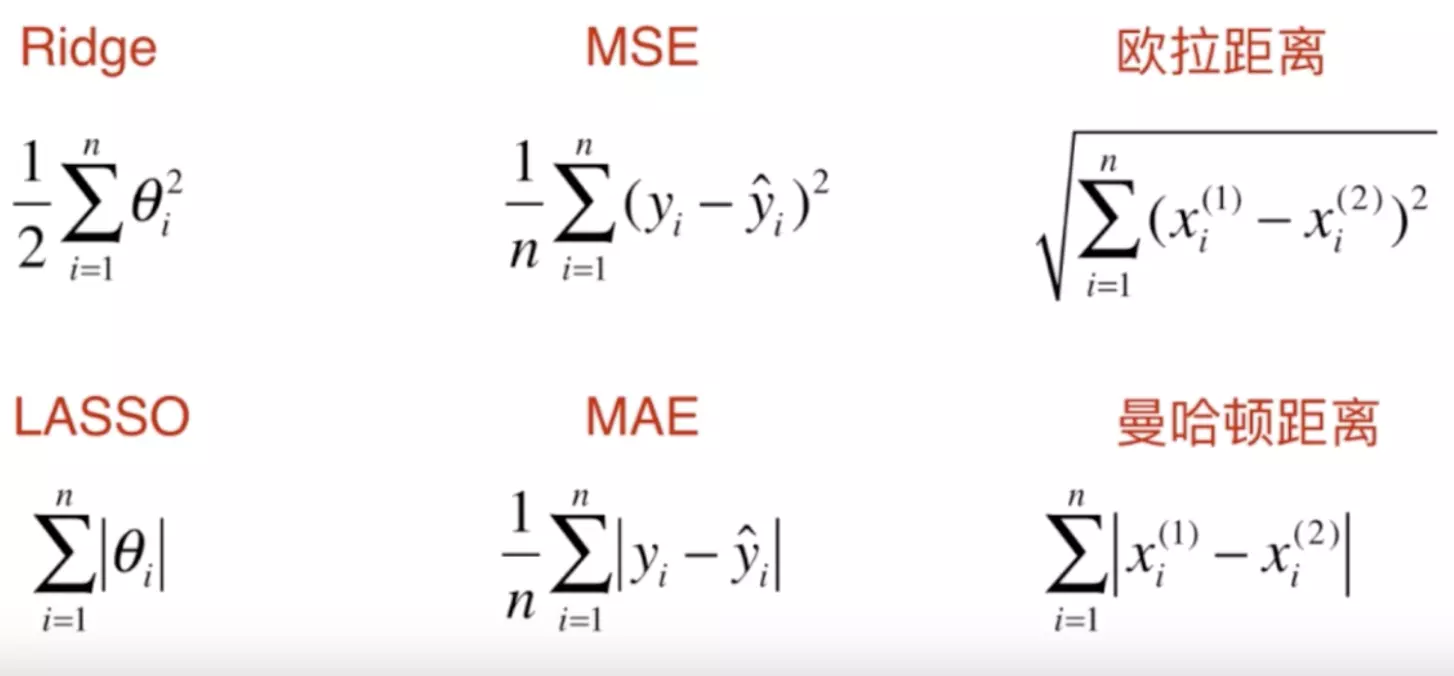
表达不同的衡量标准，但是背后的数学思想非常相似，表达出来的数学含义近乎一致。

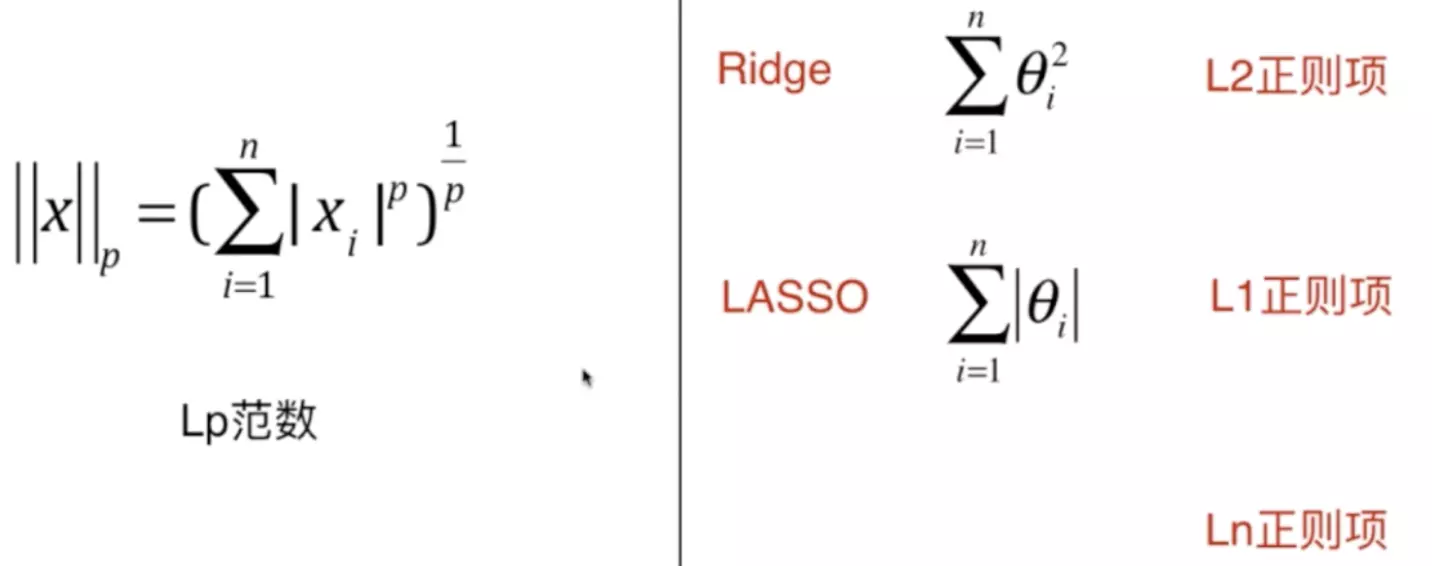
• Ridge & LASSO ：衡量正则化

• MSE & MAE：衡量回归结果的好坏

• 欧拉距离 & 曼哈顿距离：衡量两点之间距离的大小

---

L0 正则

$J( heta)= МЅЕ(у, hat{y}у; heta)+ mіn{非0 heta} $

实际用L1取代，因为L0正则的优化是一个NP难的问题

---

弹性网 Elastoc Net

结合 L1 和 L2 正则项，添加比例 r。

---

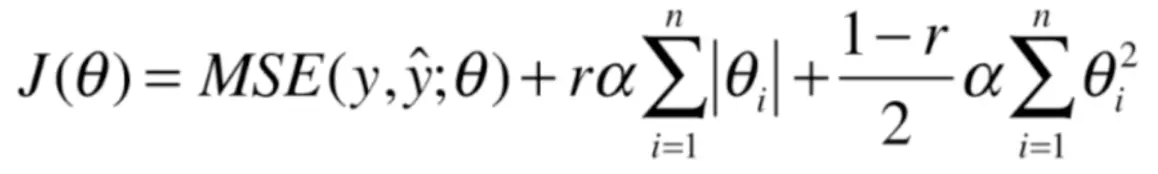
代码实现

import numpy as np
import matplotlib.pyplot as plt
 
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
 
plt.scatter(x, y)
plt.show()

---

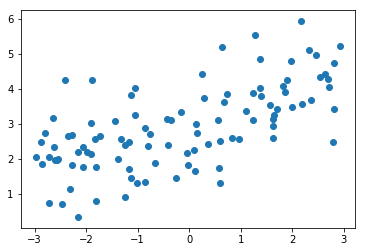
from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
 
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
# 167.94010867293571
 
def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

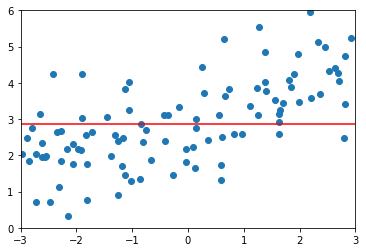
    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(poly_reg)

---

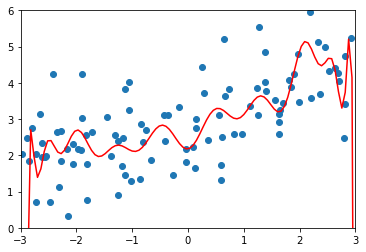
from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])
 
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)

y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
# 1.1496080843259966
 
plot_model(lasso1_reg)

---

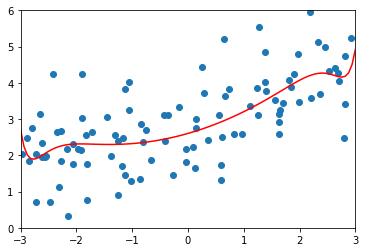
lasso2_reg = LassoRegression(20, 0.1)
lasso2_reg.fit(X_train, y_train)

y2_predict = lasso2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# 1.1213911351818648
 
plot_model(lasso2_reg)

---

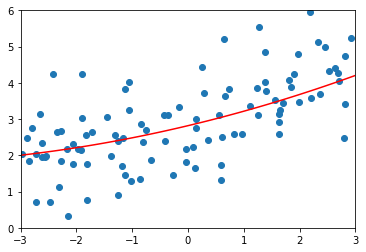
lasso3_reg = LassoRegression(20, 1)
lasso3_reg.fit(X_train, y_train)

y3_predict = lasso3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)
# 1.8408939659515595
 
plot_model(lasso3_reg)

---