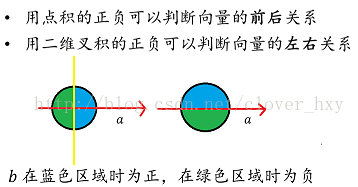
向量的板子
#include<bits/stdc++.h>
#define I inline
using namespace std;
typedef double DB;
struct Vec{
DB x,y;
I Vec(){x=y=0;}
I Vec(DB a){x=a;y=0;}
I Vec(DB a,DB b){x=a;y=b;}
I friend istream&operator>>(istream&cin,Vec&a){return cin>>a.x>>a.y;}
I friend ostream&operator<<(ostream&cou,Vec a){return cou<<a.x<<' '<<a.y;}
I Vec operator-(){return Vec(-x,-y);}
I Vec operator+(Vec a){return Vec(x+a.x,y+a.y);}
I Vec operator-(Vec a){return Vec(x-a.x,y-a.y);}
I Vec operator*(DB a){return Vec(x*a,y*a);}
I Vec operator/(DB a){return Vec(x/a,y/a);}
I friend Vec operator*(DB a,Vec b){b.x*=a,b.y*=a;return b;}
I friend Vec operator/(DB a,Vec b){b.x/=a,b.y/=a;return b;}
I Vec&operator+=(Vec a){x+=a.x,y+=a.y;return*this;}
I Vec&operator-=(Vec a){x-=a.x,y-=a.y;return*this;}
I Vec&operator*=(DB a){x*=a,y*=a;return*this;}
I Vec&operator/=(DB a){x/=a,y/=a;return*this;}
I DB operator*(Vec a){return x*a.x+y*a.y;}
I DB operator^(Vec a){return x*a.y-y*a.x;}
I friend bool operator<(Vec a,Vec b){
return (a^b)>0||((a^b)==0&&Len(a)<Len(b));
}
I friend DB Len(Vec a){
return sqrt(a.x*a.x+a.y*a.y);
}
I friend Vec Turn(Vec a,DB r){
const DB c=cos(r),s=sin(r);
return Vec(a.x*c-a.y*s,a.y*c+a.x*s);
}
};
初阶
向量运算
点积:(x_1x_2+y_1y_2),是一个向量在另一个向量上的投影
叉积:(x_1y_2-x_2y_1),是两个向量形成的平行四边形的有向面积
用途很广,搬一张图
旋转公式
((x,y))转(r)弧度( ightarrow(xcos r-ysin r,ycos r+xsin r))
点到直线距离
算一个叉积,除以底边长就得到了高,也就是点到直线距离。
DB Dis(Vec&a,Vec&b1,Vec&b2){
return fabs((b1-a)^(b2-a))/Len(b1-b2);
}
直线交点&线段交点
点斜式要各种特判,不是理想的实现方法
考虑这样的转化方式:叉积->面积比->高的比->长度比->坐标
如下图,两直线相交于(P),(F)和(G)是垂足,有( riangle A_1PFsim riangle CB_1G),可以推出
而(P=A_1+frac{|A_1P|}{|vec a|}vec{a}),然后就做出来了。
蒟蒻到现在好像还是背不了代码,只能背下面这张图了TAT

如何判断线段相交呢?先把直线交点求出来,再点积判一下位置关系不就好啦
Vec LineCross(Vec a1,Vec a2,Vec b1,Vec b2){
a2-=a1;b2-=b1;
return b2^a2?a1+(b2^(b1-a1))/(b2^a2)*a2:Vec(NAN,NAN);
}
Vec SegCross(Vec&a1,Vec&a2,Vec&b1,Vec&b2){
Vec c=LineCross(a1,a2,b1,b2);
return (a1-c)*(a2-c)>0||(b1-c)*(b2-c)>0?Vec(NAN,NAN):c;
}
判断点是否在多边形内
过点任作一条射线(当然平行坐标轴的最方便啦),与多边形交奇数次则在多边形内。
凸包
极角排序
可以用atan2,也可以直接用叉积判断。
把最下面的点的坐标找出来,把所有点整体平移,这时候所有点都不在(x)轴下面了,在(180°)内叉积可以起到比较方向的作用。
代码见凸包部分。
求凸包
单调栈维护。如图,((P_i-P_{t-1})×(P_t-P_{t-1})ge0),则(P_t)不在凸包上,需要弹掉。

洛谷P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows
I bool Polar(Vec&a,Vec&b){return (a^b)>0||((a^b)==0&&Len(a)<Len(b));}
//即Vec模板里重载的小于号。共线向量把短的放前面,求凸包的时候方便弹掉
I int Convex(Vec*a,Vec*e){
R n=e-a,k=0;
for(R i=1;i<n;++i)
if(a[i].y<a[k].y||(a[i].y==a[k].y&&a[i].x<a[k].x))k=i;
swap(a[0],a[k]);
const Vec tmp=a[0];
for(R i=0;i<n;++i)a[i]-=tmp;
sort(a+1,a+n,Polar);
R*st=new int[n],p=0;
for(R i=1;i<n;st[++p]=i++)
while(p&&((a[i]-a[st[p-1]])^(a[st[p]]-a[st[p-1]]))>=0)--p;
for(R i=0;i<=p;++i)a[i]=a[st[i]]+tmp;
return p+1;
}
int main(){
R n;cin>>n;
for(R i=1;i<=n;++i)cin>>a[i];
n=Convex(a+1,a+n+1);
DB ans=Len(a[1]-a[n]);
for(R i=1;i<n;++i)ans+=Len(a[i+1]-a[i]);
printf("%.2lf
",ans);
return 0;
}
判断点是否在凸包内
需要令凸包最下面的点为((0,0)),不要还原。
把点的坐标也做相应的变换之后,丢进数组里lower_bound找到与它极角最接近的两个点形成的线段,叉积判即可。
bool Inside(Vec*a,Vec*e,Vec v){
R i=lower_bound(a,e,v)-a-1;
return ((a[i+1]-a[i])^(v-a[i]))>=0;
}
多边形面积
对于凸多边形的理解:将多边形划分成若干个三角形,每个三角形的面积是两个向量叉积的(frac12)。
update:其实任意多边形面积都可以用三角剖分法求,详见洛谷日报 计算几何初步 by wjyyy。
DB PolygonArea(Vec*a,Vec*e){
R n=e-a;DB s=0;
for(R i=2;i<n;++i)s+=(a[i-1]-a[0])^(a[i]-a[0]);
return s/2;
}
进阶算法
凸包
旋转卡壳
利用凸包的单调性,在枚举点的时候更新决策点(对踵点)并更新答案。
洛谷P1452 Beauty Contest
int main(){
R n;cin>>n;
for(R i=1;i<=n;++i)cin>>a[i];
n=Convex(a+1,a+n+1);
DB ans=0;
a[++n]=a[1];//最后加一个点
for(R i=1,p=1;i<n;++i){
while(Dis(a[p],a[i],a[i+1])<Dis(a[p+1],a[i],a[i+1]))p=p%n+1;
ans=max(ans,max(Len2(a[p]-a[i]),Len2(a[p]-a[i+1])));
}
printf("%.0lf
",ans);
return 0;
}
半平面交
XZY巨佬提到了一种(O(n^2))的算法。其实,如果不是在线插入的话,可以做到(O(nlog n))。
我们用有向直线(一个点和一个方向向量)表示半平面,以下默认半平面在有向直线的左侧。
对有向直线按方向向量的极角排序,维护一个双端队列,存储当前构成半平面的直线以及相邻两直线的交点。
每次加入一条有向直线,如果队首/队尾的交点在直线右侧(用叉积判)则弹掉队首/队尾的直线。
为什么这样是对的呢?因为加入直线的单调性,所以要被弹出的直线一定在队首或队尾。感兴趣的话可以自己手画一些例子来理解。
需要注意的细节:
- 加入直线时,先弹队尾,再弹队首。
- 最后还要检查队尾交点是否在队首直线的右侧,如果是也要弹掉。
- 特判平行直线,在右侧的要弹掉。
- 如果题目给出的半平面不一定有限制边界,则应该手动加入一个INF边界。
另有洛谷P3222 [HNOI2012]射箭 的题解
模板题:洛谷P4196 [CQOI2006]凸多边形
struct Line{
Vec p,v;DB ang;
I Line(){}
I Line(Vec a,Vec b){p=a,v=b-a,ang=atan2(v.y,v.x);}
I bool operator<(Line&a){return ang<a.ang;}
I bool Right(Vec&a){return (v^(a-p))<-EPS;}
I friend Vec Cross(Line&a,Line&b){return a.p+(b.v^(b.p-a.p))/(b.v^a.v)*a.v;}
}a[N],q[N];
DB HalfPlane(Line*a,Line*e){
R n=e-a,h=0,t=0;
sort(a,e);q[0]=a[0];
for(R i=1;i<n;++i){
while(h<t&&a[i].Right(k[t-1]))--t;
while(h<t&&a[i].Right(k[h]))++h;
if(q[t].ang!=a[i].ang)q[++t]=a[i];
else if(a[i].Right(q[t].p))q[t]=a[i];
if(h<t)k[t-1]=Cross(q[t-1],q[t]);
}
while(h<t&&q[h].Right(k[t-1]))--t;
k[t]=Cross(q[t],q[h]);
return PolygonArea(k+h,k+t+1);
}
int main(){
R n,m,t=0;
cin>>n;
for(R i=1;i<=n;++i){
Vec fst,lst,now;
cin>>m>>fst;lst=fst;
for(R j=2;j<=m;++j)
cin>>now,a[++t]=Line(lst,now),lst=now;
a[++t]=Line(lst,fst);
}
printf("%.3lf
",HalfPlane(a+1,a+t+1));
return 0;
}
闵可夫斯基和
对于欧氏空间的两个点集(A,B),其闵可夫斯基和为点集(C={a+b|ain A,bin B})
其中加法就是向量加法。
接下来我们只讨论凸包的闵可夫斯基和。

一个四边形,一个三角形,两个凸包的闵可夫斯基和会长什么样子呢?
因为凸包的特性,我们只需要取其中一个凸集所有最外层的点,将另一个凸多边形沿这个点向量移动,就可以得到闵可夫斯基和。

观察一下它的特点:外面正好有(7)个点,(7)条边,有没有注意到(7=4+3)呢?
实际上,对于任意两个凸包来说,它们的闵可夫斯基和与它们的每一条边按极角序顺次相连所得的图形都是全等的,也是一个凸包。
那岂不是很好求?二路归并即可。需要处理三点共线的情况,了撇一点的话直接扔进Convex函数里再求一遍凸包就好了。
洛谷P4557 [JSOI2018]战争
typedef long long DB;//不涉及小数运算,直接开longlong
int Convex(Vec*a,Vec*e,Vec&bs){
R n=e-a,k=0,p=0;
for(R i=1;i<n;++i)
if(a[i].y<a[k].y||(a[i].y==a[k].y&&a[i].x<a[k].x))k=i;
swap(a[0],a[k]);bs+=a[0];
for(R i=n-1;~i;--i)a[i]-=a[0];
sort(a,e);
for(R i=1;i<n;st[++p]=i++)
while(p&&((a[i]-a[st[p-1]])^(a[st[p]]-a[st[p-1]]))>=0)--p;
for(R i=0;i<=p;++i)a[i]=a[st[i]];//做出来没还原
return a[p+1]=0,p+1;
}
void Minkowski(R n,R m){
for(R i=n;i;--i)a[i]-=a[i-1];
for(R j=m;j;--j)b[j]-=b[j-1];
for(R i=1,j=1,k=0;i<=n||j<=m;++k)
c[k]=c[k-1]+(i<=n&&(j>m||a[i]<b[j])?a[i++]:b[j++]);
}
int main(){
ios::sync_with_stdio(0);
R n=in(),m=in(),q=in();
Vec bs=0,v;
for(R i=0;i<n;++i)cin>>a[i];
for(R i=0;i<m;++i)cin>>b[i],b[i]=-b[i];
n=Convex(a,a+n,bs);
m=Convex(b,b+m,bs);
Minkowski(n,m);
n=Convex(c,c+n+m+1,v);
while(q--)
cin>>v,cout<<Inside(c,c+n,v-bs)<<'
';
return 0;
}
其它
最小圆覆盖
把点集random_shuffle
第一层枚举一个点,如果不在当前圆中,令其为圆心,半径设为(0)。
第二层枚举另一个点,如果不在当前圆中,将圆更新为以当前两个点的连线为直径的圆。
第三层枚举另一个点,如果不在当前圆中,将圆更新为当前三个点的外接圆。
期望复杂度(O(n))。
洛谷P1742 最小圆覆盖
typedef long double DB;//此题略卡精度
I void PerpLine(Vec a1,Vec a2,Vec&b1,Vec&b2){//中垂线
b1=(a1+a2)/2;b2=b1+Turn(a1-a2);
}
I void CircleCoverage(Vec*a,Vec*e,Vec&O,DB&r){
R n=e-a;
for(R i=0;i<n;++i){
if(Len(a[i]-O)<=r)continue;
O=a[i],r=0;
for(R j=0;j<i;++j){
if(Len(a[j]-O)<=r)continue;
O=(a[i]+a[j])/2,r=Len(a[i]-a[j])/2;
Vec a2=O+Turn(a[i]-a[j]),b1,b2;
for(R k=0;k<j;++k){
if(Len(a[k]-O)<=r)continue;
PerpLine(a[i],a[k],b1,b2);
O=LineCross(O,a2,b1,b2),r=Len(a[i]-O);
}
}
}
}
int main(){
R n;cin>>n;
for(R i=1;i<=n;++i)cin>>a[i];
srand(20020307);
random_shuffle(a+1,a+n+1);
Vec O;DB r=0;
CircleCoverage(a+1,a+n+1,O,r);
cout<<fixed<<setprecision(10)<<r<<endl<<O<<endl;
return 0;
}
自适应辛普森积分
求函数的定积分,应用于算不规则图形的面积。采用二次函数来拟合。
不断分割区间并迭代,直到误差控制在EPS以内。
因为误差和区间长度有关,所以可以将EPS也进行迭代,每次除以(2)。
洛谷P4526 【模板】自适应辛普森法2
#include<bits/stdc++.h>
#define DB double
using namespace std;
DB a,EPS=1e-6;
inline DB f(DB x){
return pow(x,a/x-x);
}
inline DB Calc(DB l,DB r){
return (r-l)*(f(l)+f(r)+4*f((l+r)/2))/6;
}
DB Simpson(DB l,DB r,DB ans,DB EPS){
DB m=(l+r)/2,al=Calc(l,m),ar=Calc(m,r);
return fabs(al+ar-ans)<EPS?ans:Simpson(l,m,al,EPS/2)+Simpson(m,r,ar,EPS/2);
}
int main(){
cin>>a;
if(a<0)puts("orz");
else printf("%.5lf
",Simpson(EPS,20,Calc(0,20),EPS));
return 0;
}