大家好,我是程序员吴师兄,欢迎来到 图解剑指 Offer 结构化专栏,在这个专栏里我将和大家一起学习如何用结构化的思维来思考、解题、写代码,希望能帮助你即使在面试的时候紧张也能做对。
今天分享的题目来源于 LeetCode 上的剑指 Offer 系列 面试题 12. 矩阵中的路径。
题目汇总链接:https://www.algomooc.com/hi-offer
一、题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。
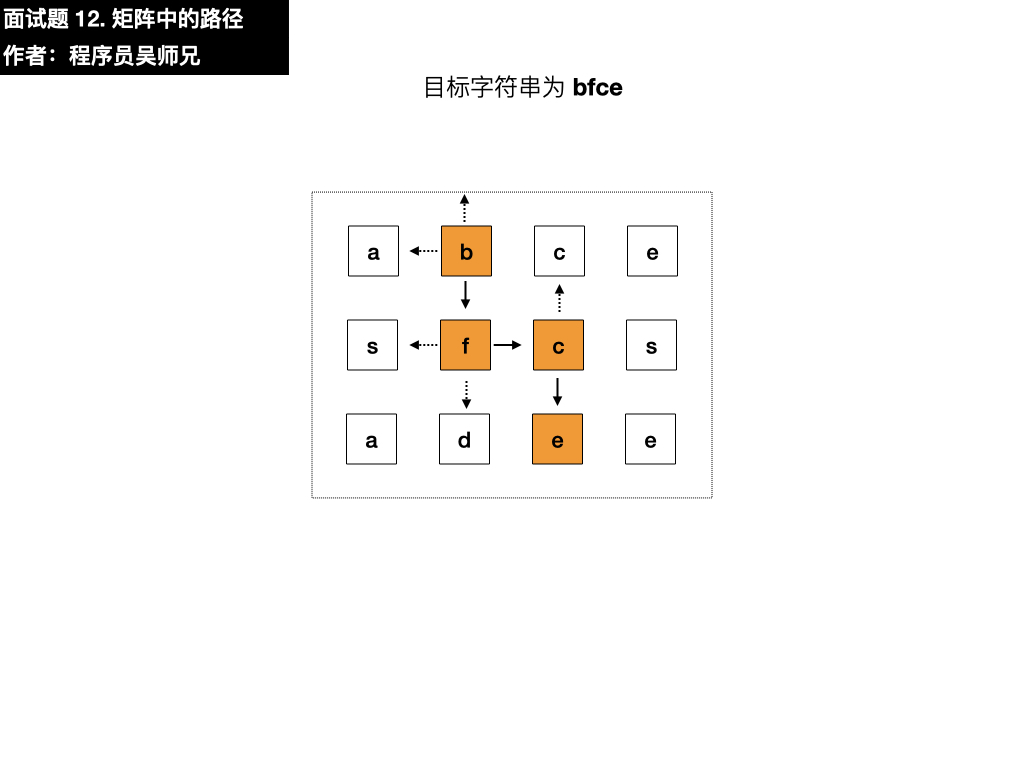
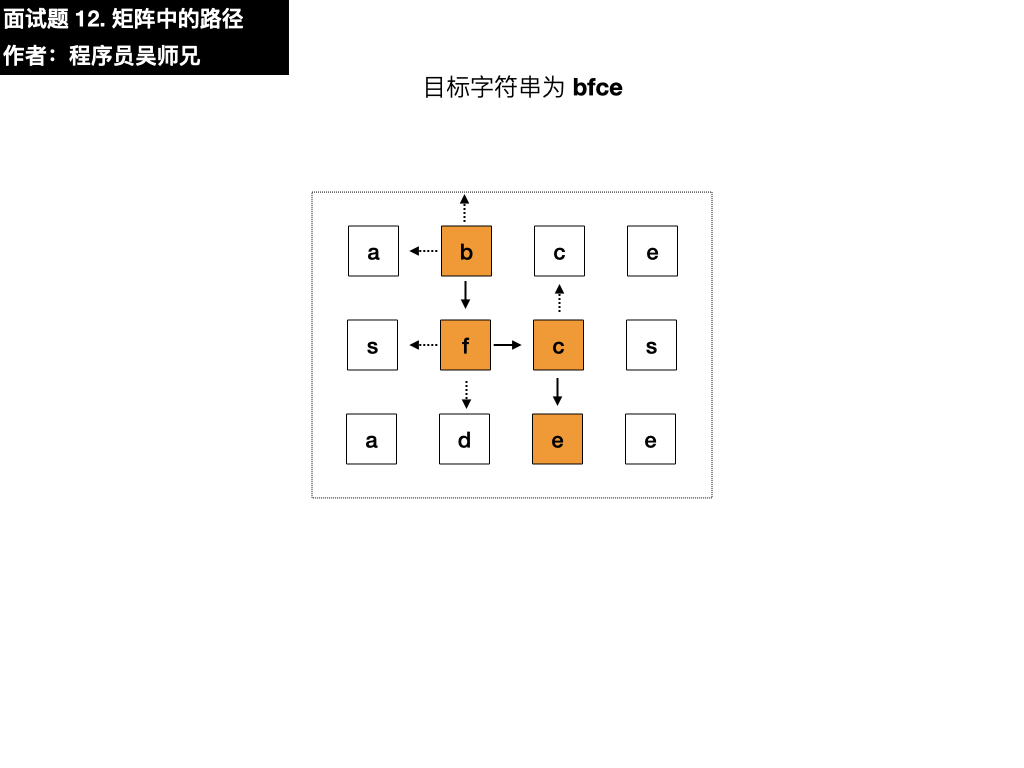
如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
提示:
1 <= board.length <= 2001 <= board[i].length <= 200
二、题目解析
我们依旧用 四步分析法 进行结构化的分析。
- 模拟:模拟题目的运行。
- 规律:尝试总结出题目的一般规律和特点。
- 匹配:找到符合这些特点的数据结构与算法。
- 边界:考虑特殊情况。
1、模拟
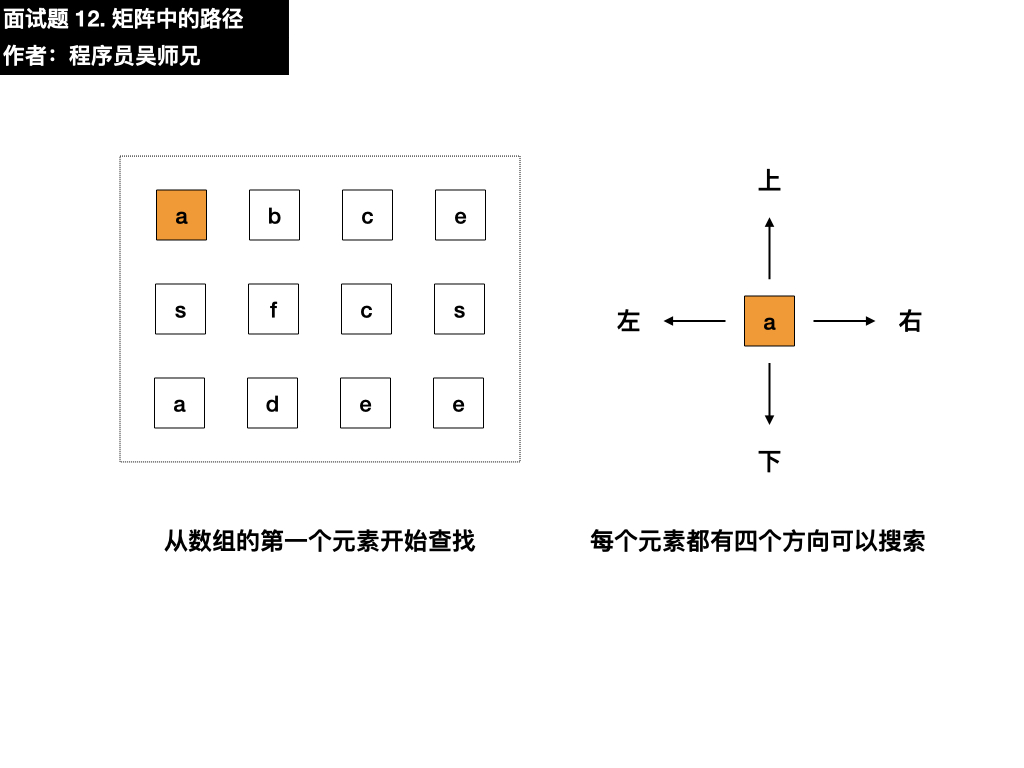
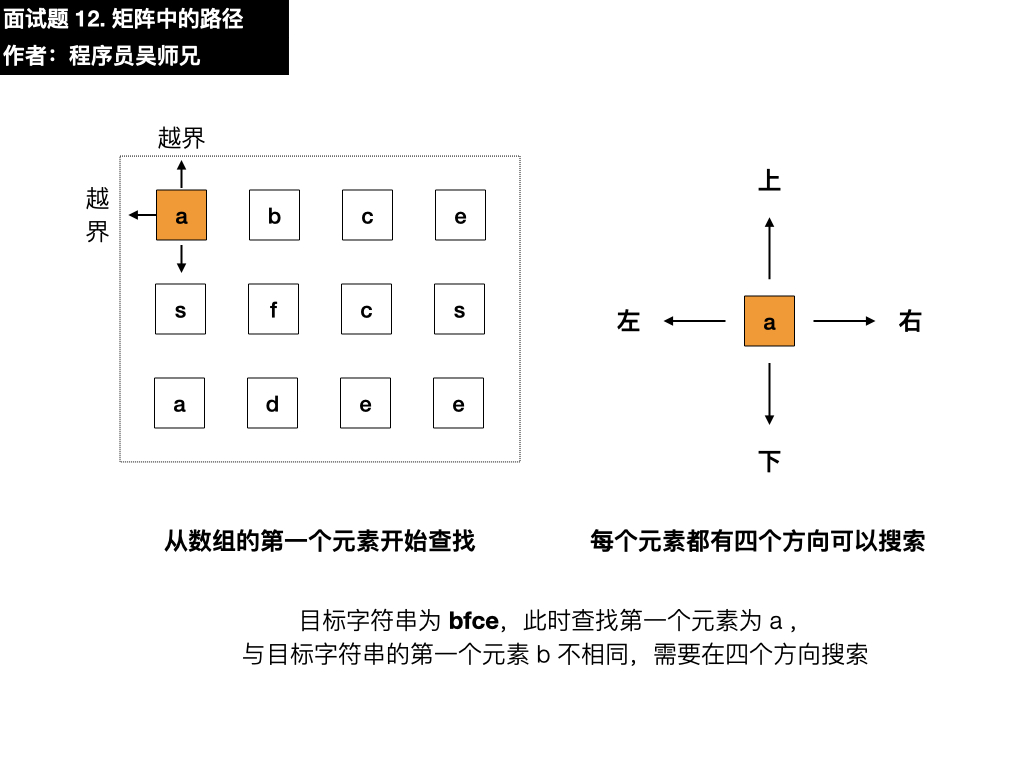
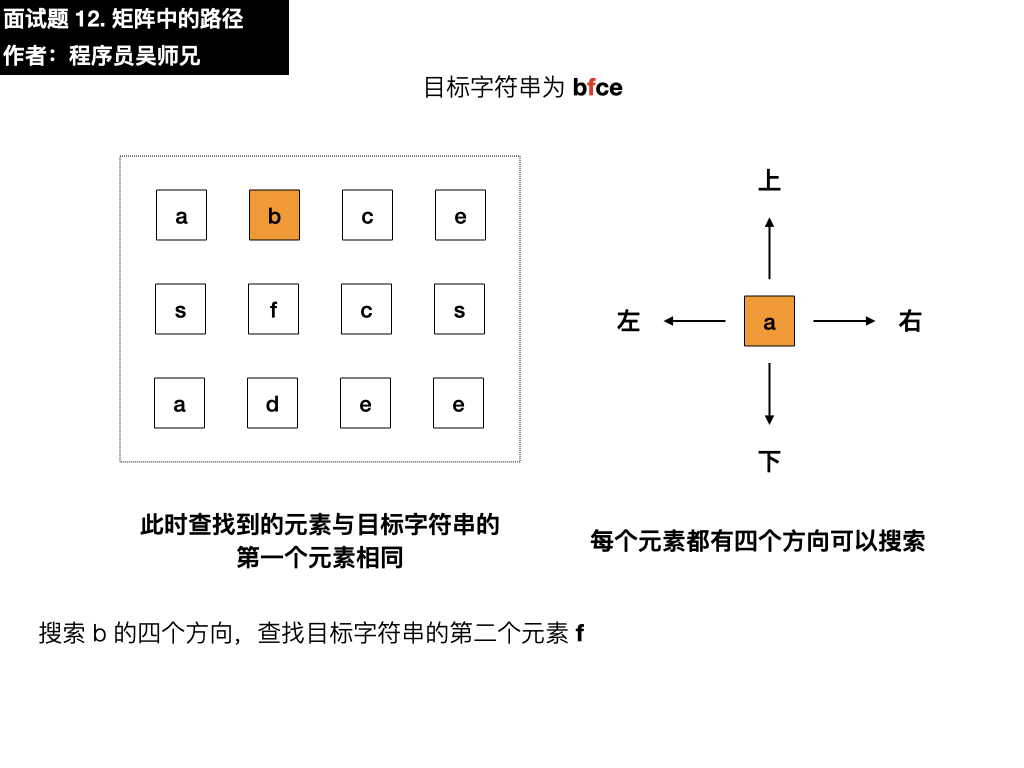
首先看一下矩阵的初始状态。

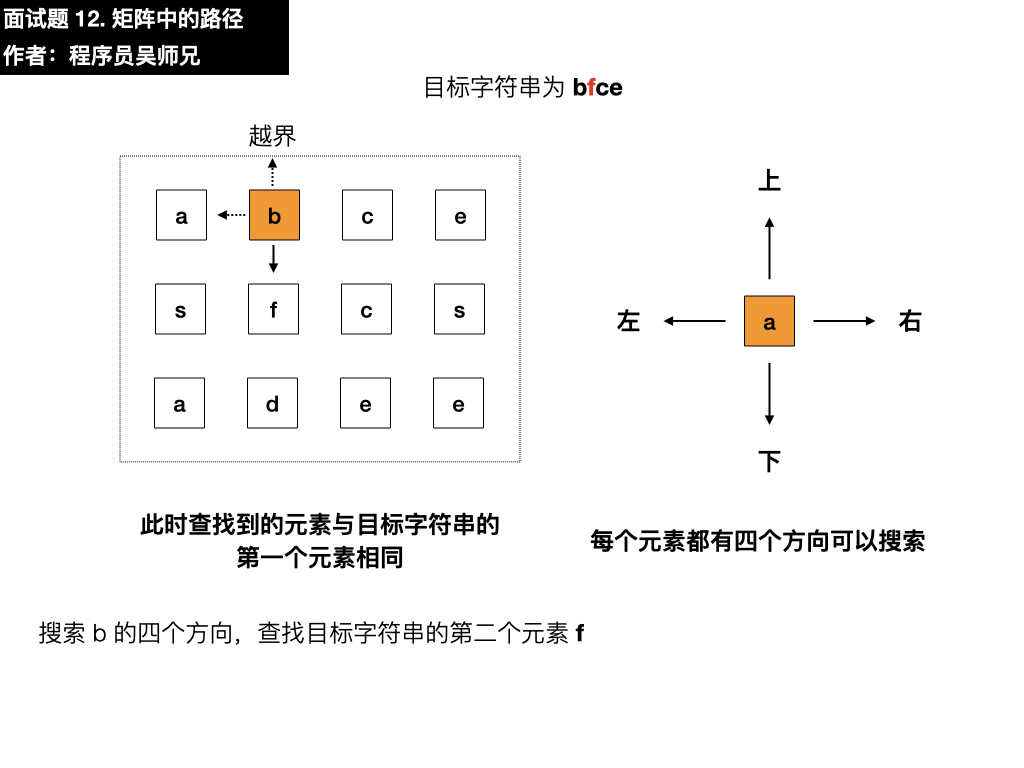
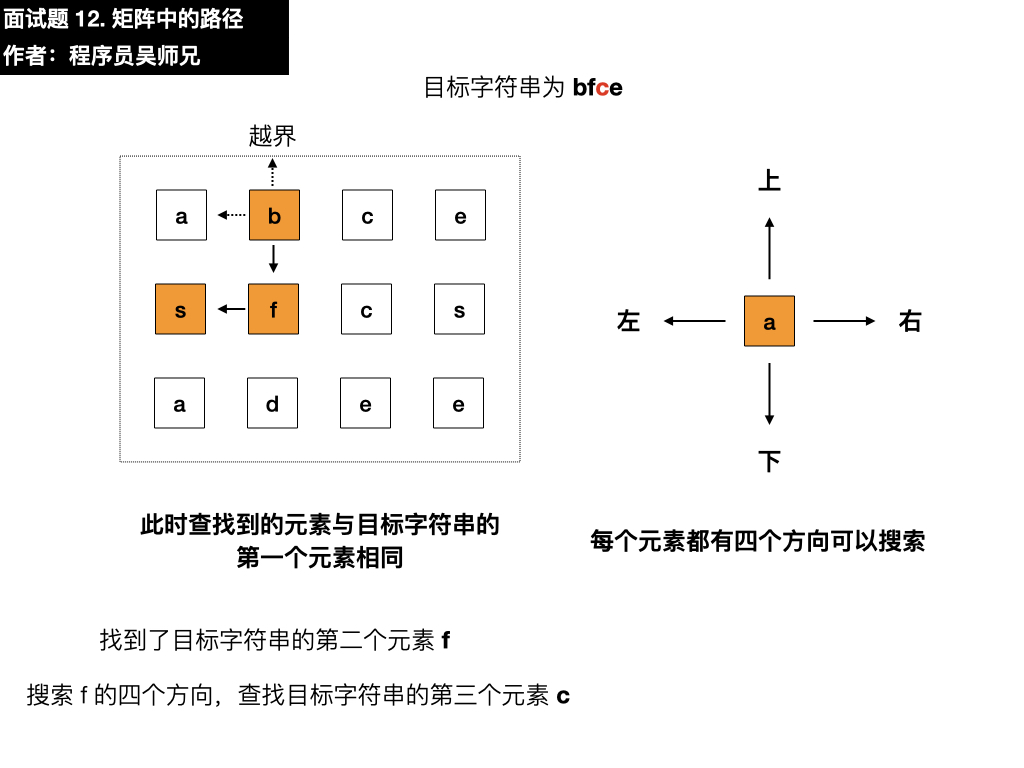
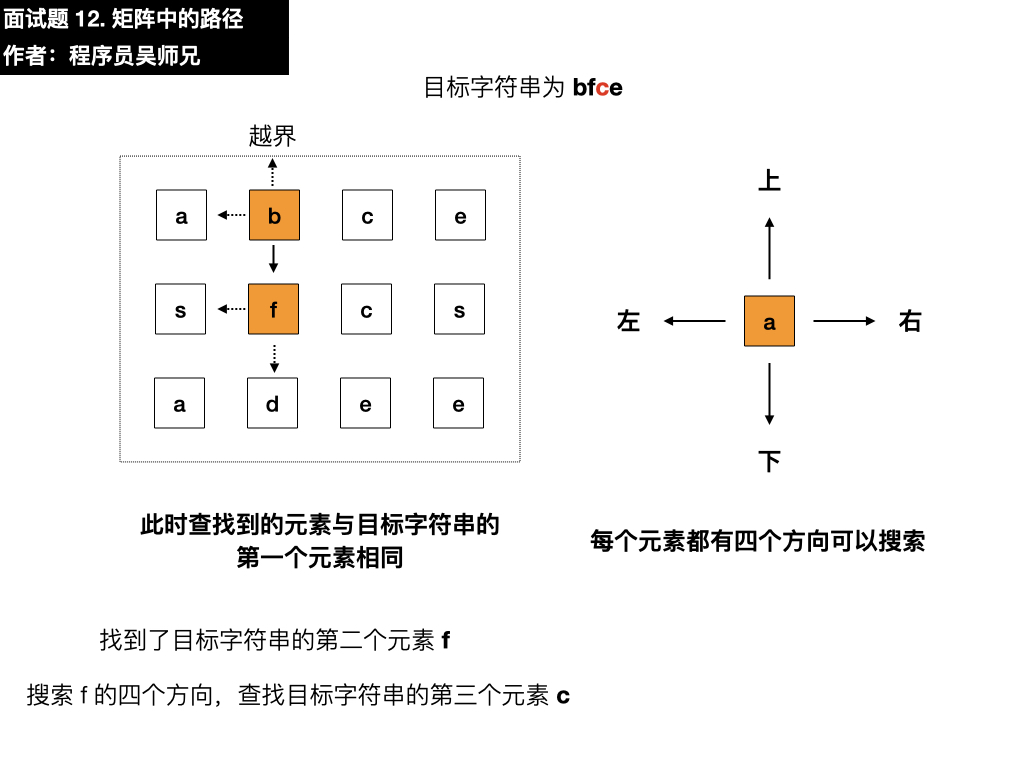
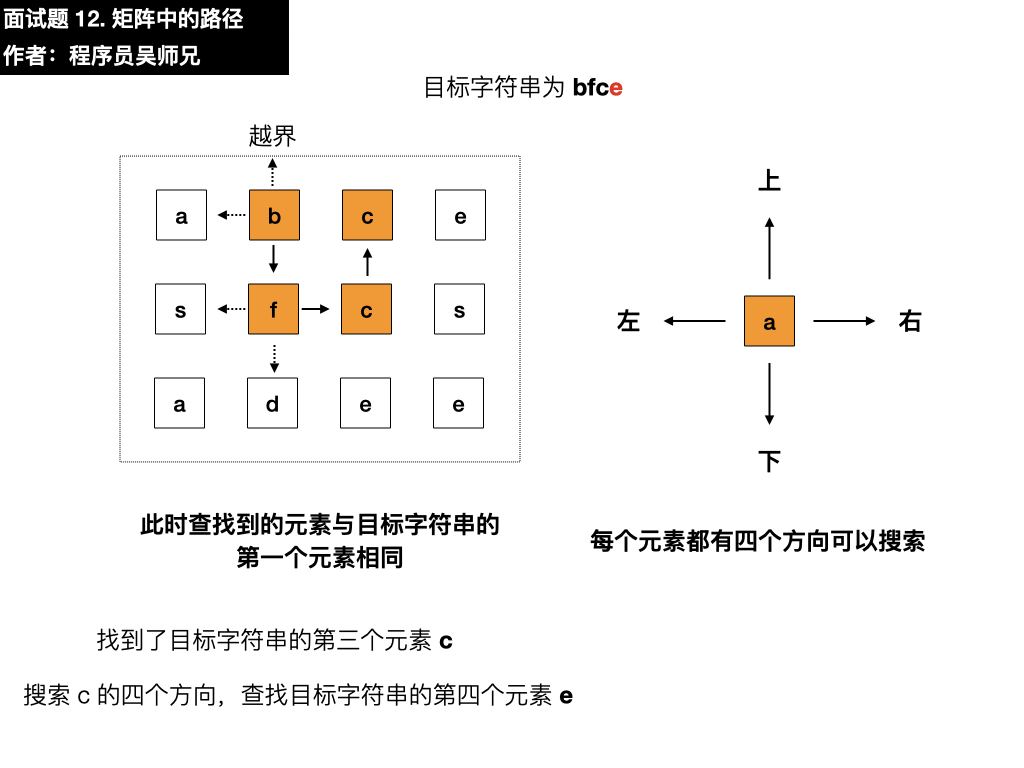
我们需要在这个矩阵中寻找目标字符串 bfce,第一步要做的就是先匹配上目标字符串的第一个元素 b ,我们从矩阵的第一行第一列的元素开始匹配,找到了 a 。

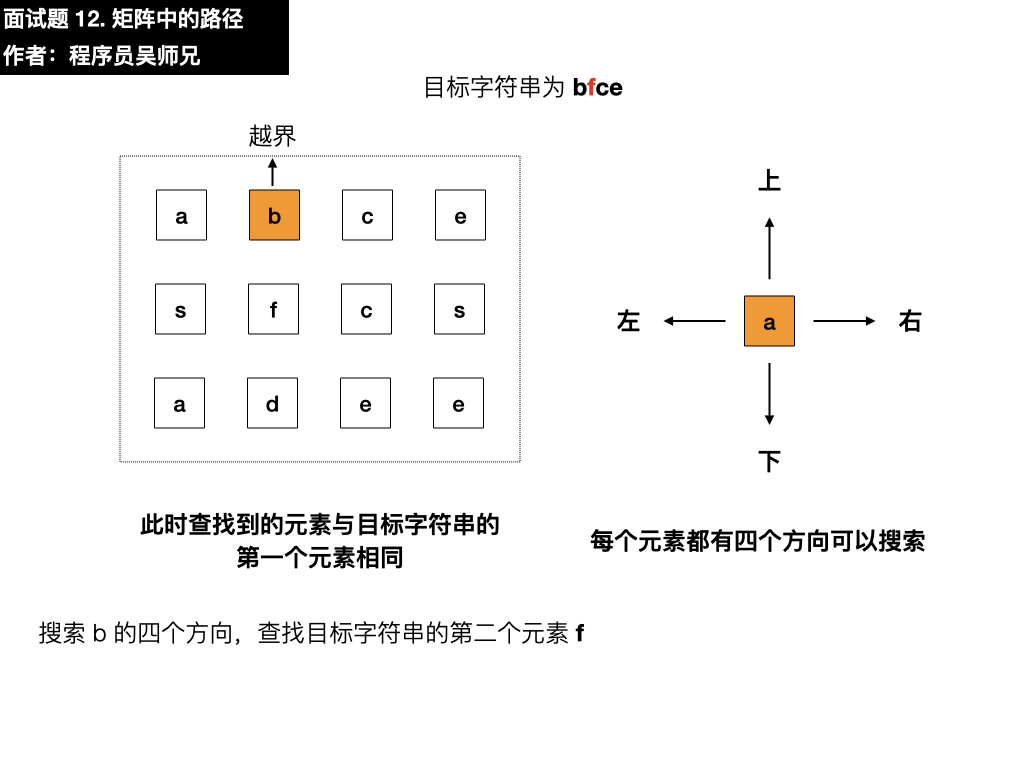
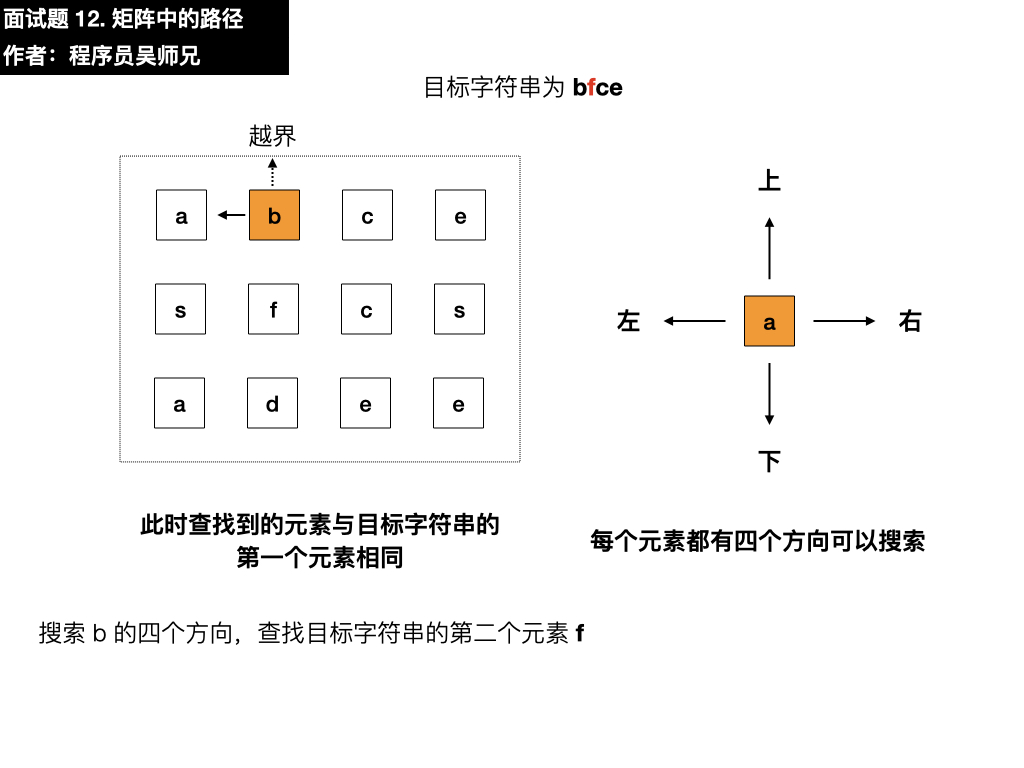
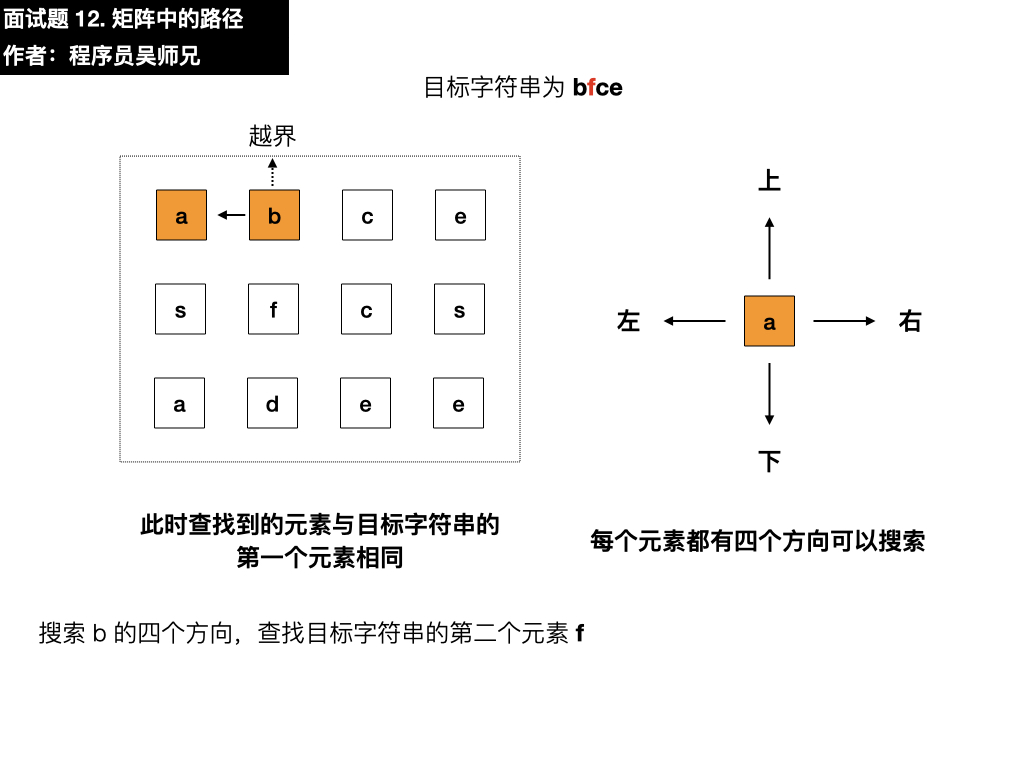
目标字符串为 bfce,此时查找第一个元素为 a ,与目标字符串的第一个元素 b 不相同,需要在四个方向搜索,看看能不能找到符合要求的元素,我们按照上左下右的顺序进行遍历寻找。
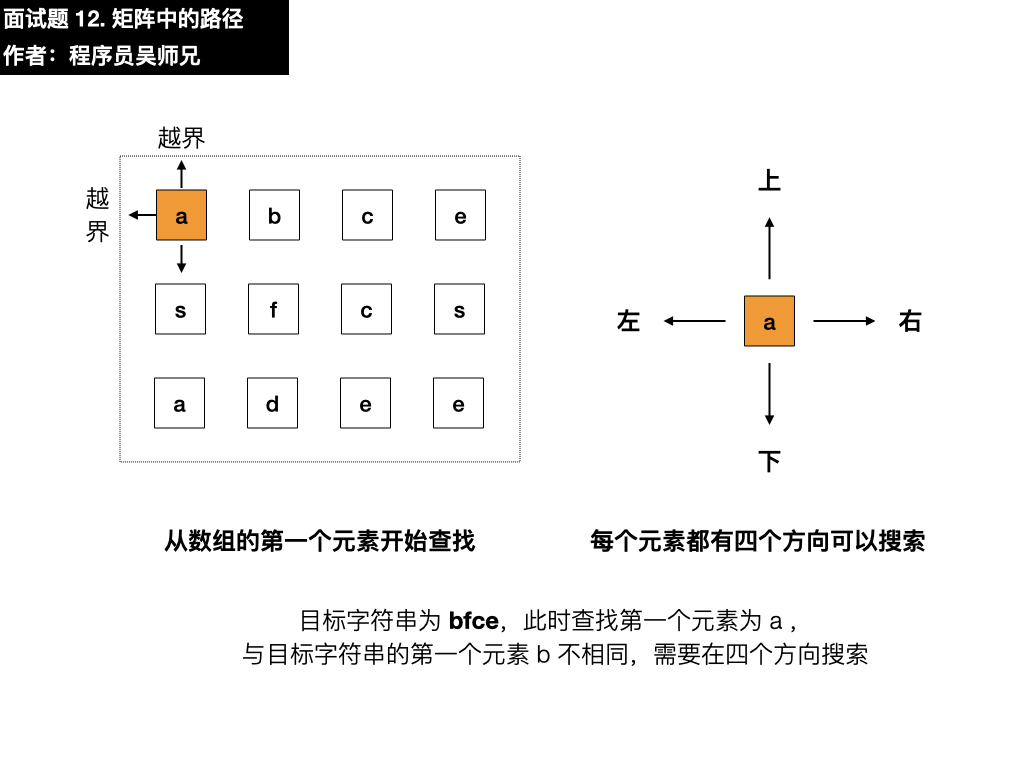
- 上:越界了
- 左:越界了
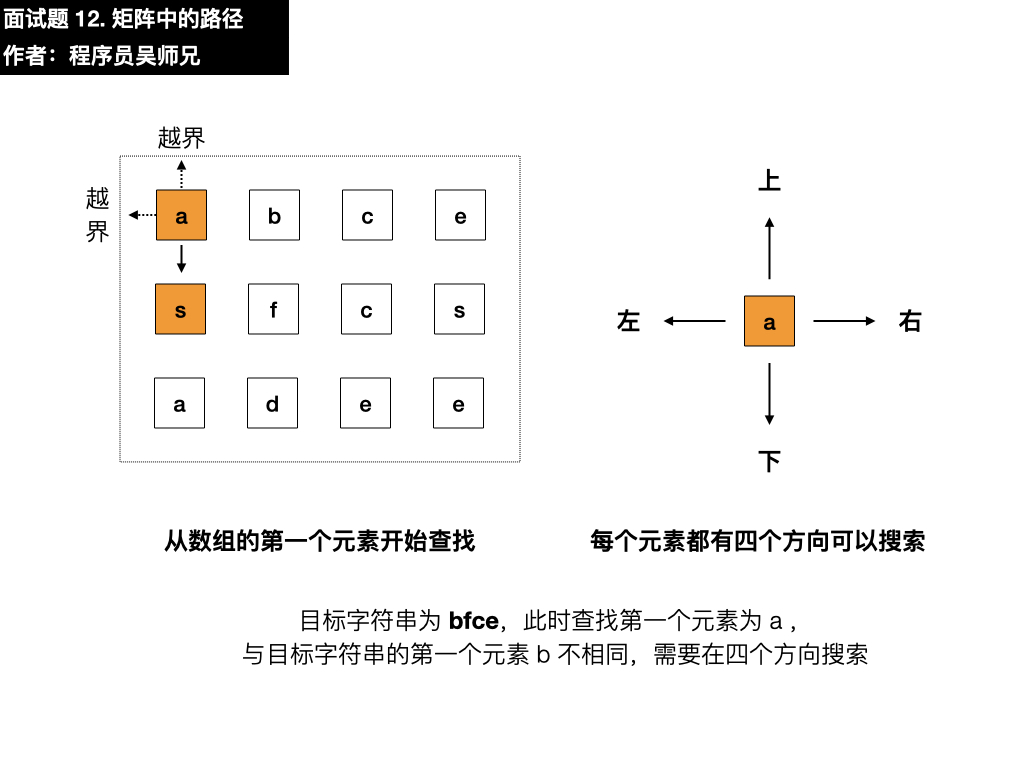
- 下:是 s ,与目标元素 b 不相同
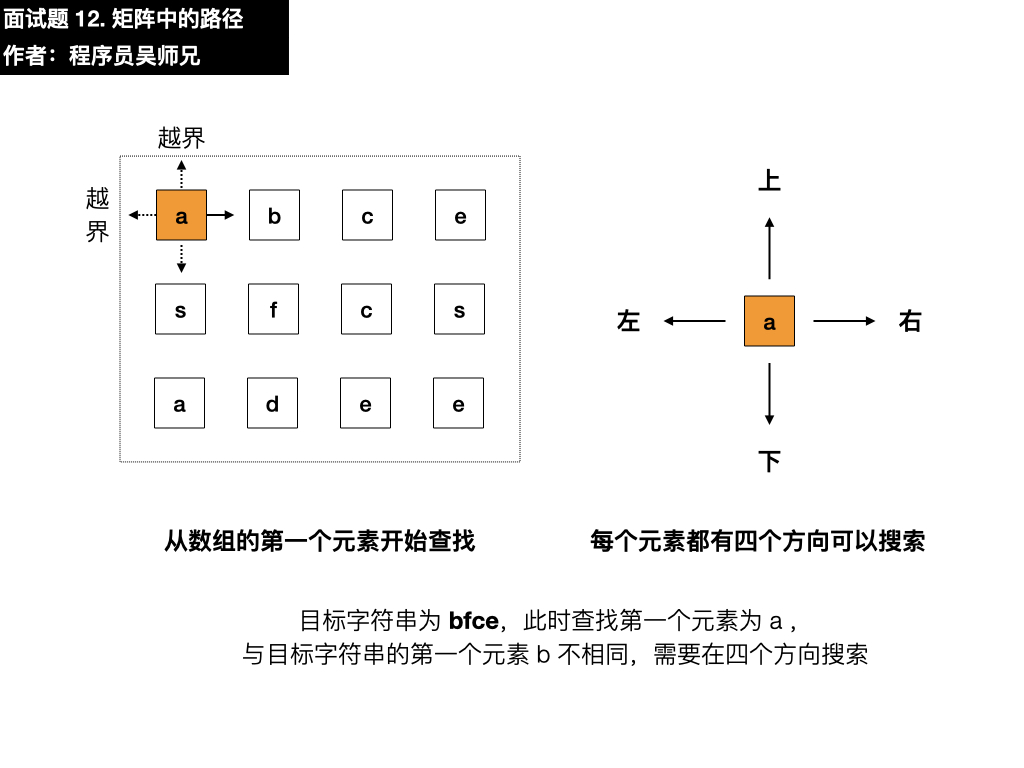
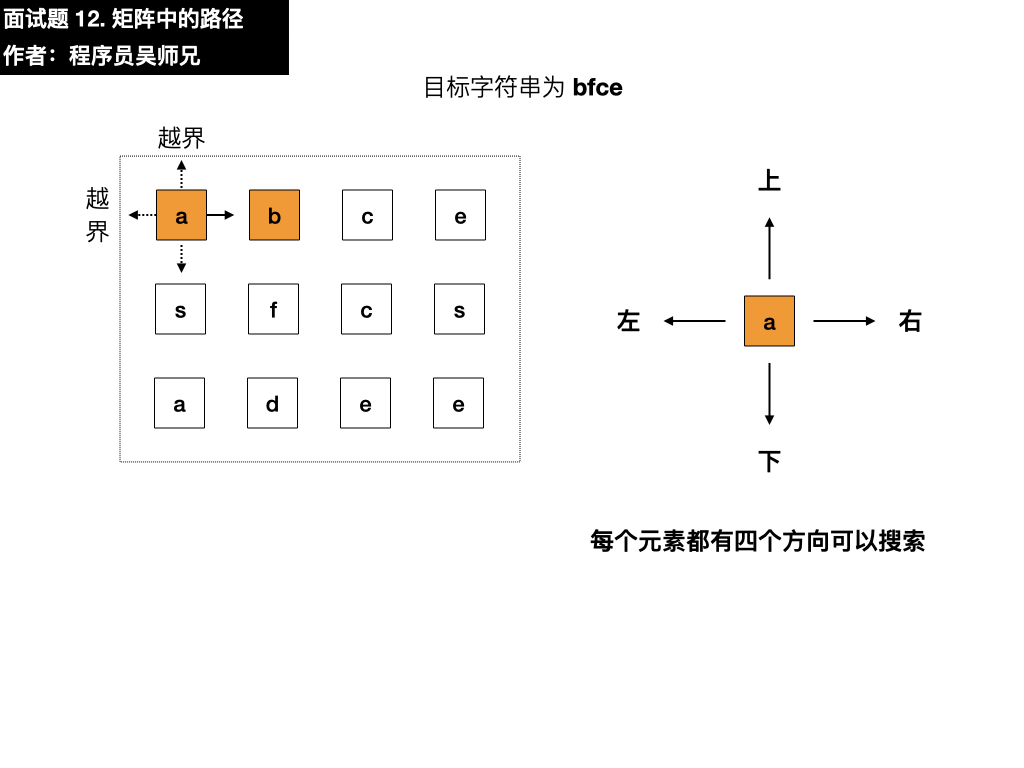
- 右:是 b,符合要求,依葫芦画瓢找第二个元素
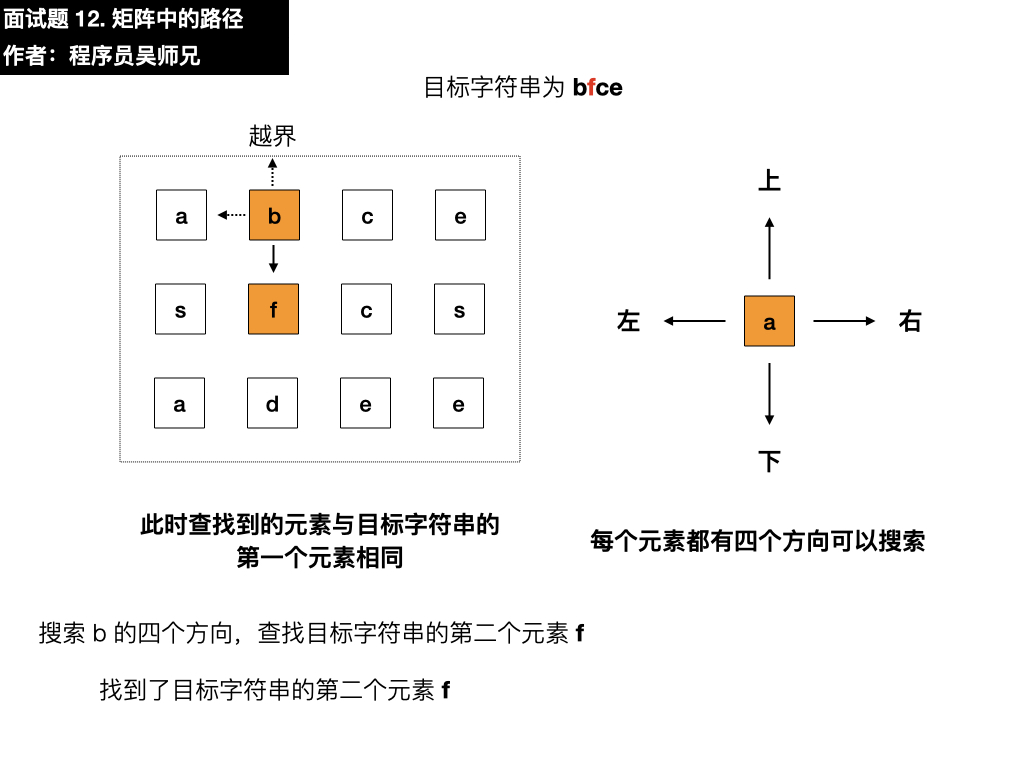
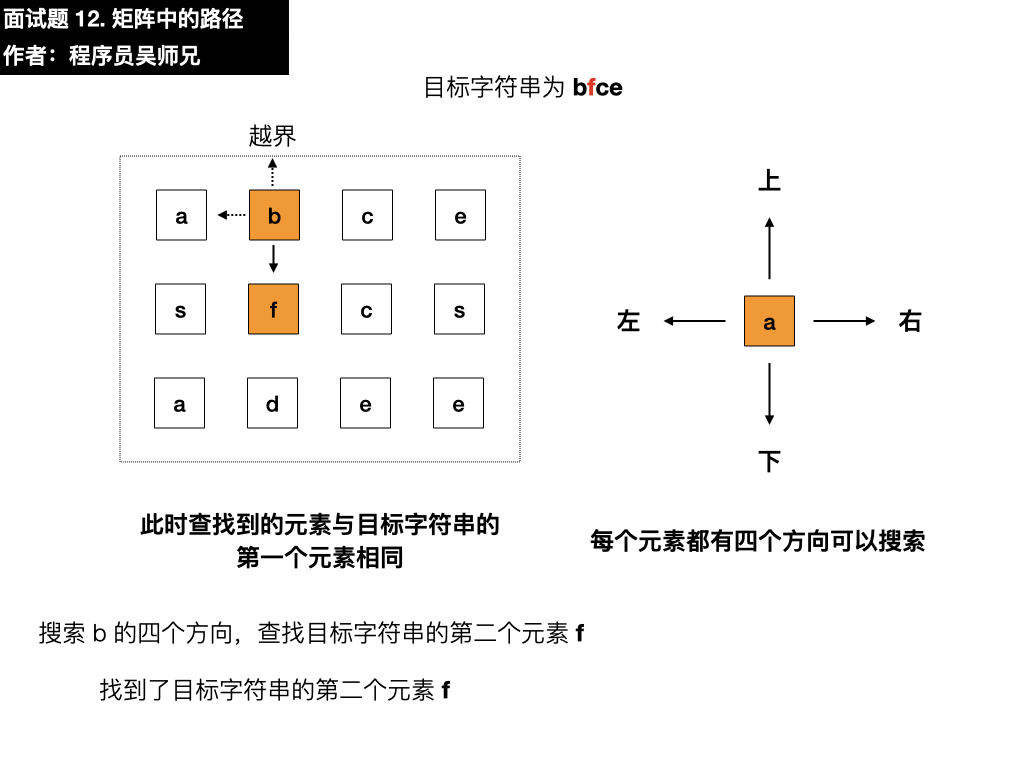
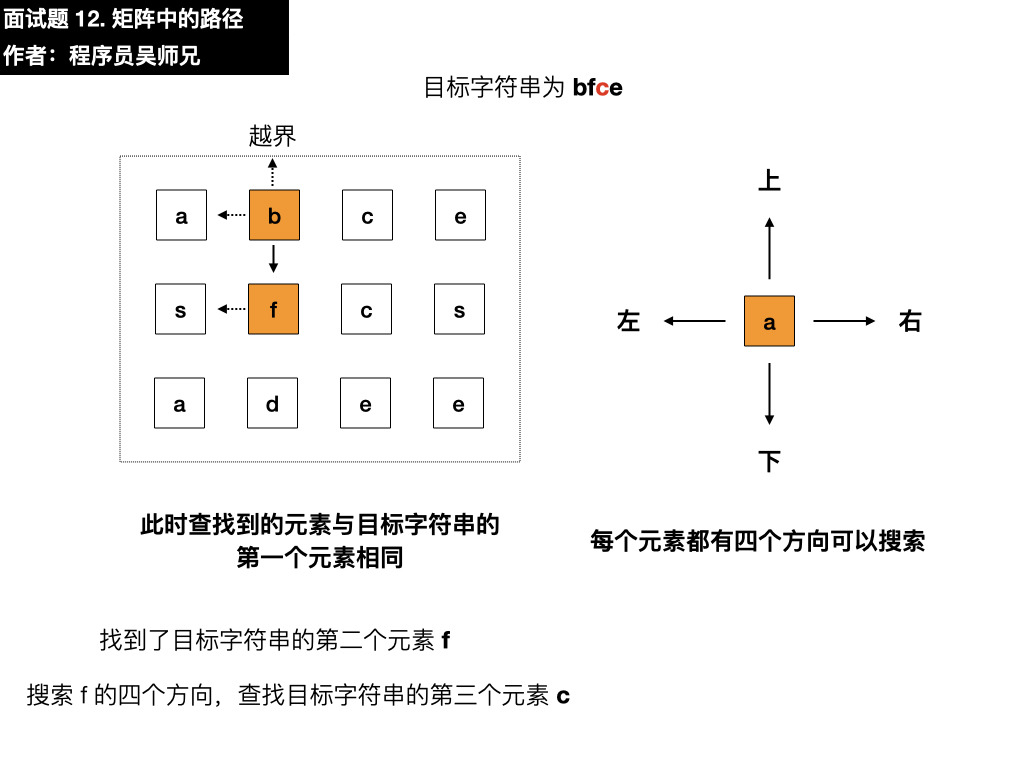
- 上:越界了
- 左:是 a,与目标元素 f 不相同
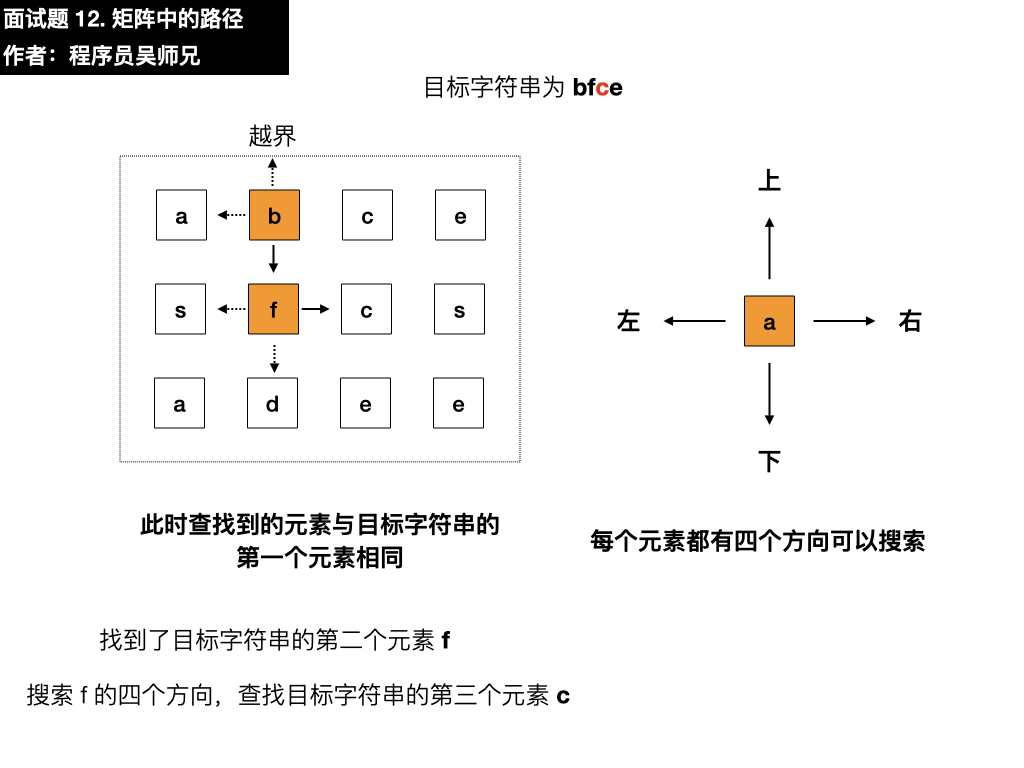
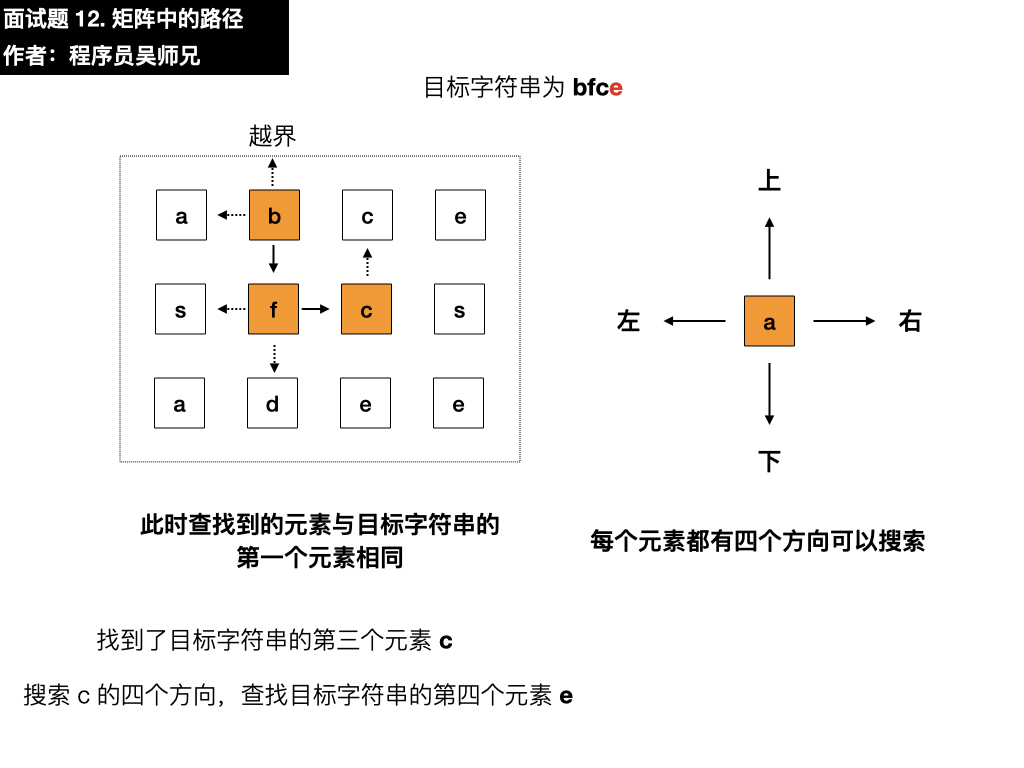
- 下:是 f,与目标元素 f 相同,符合要求,依葫芦画瓢找第三个元素
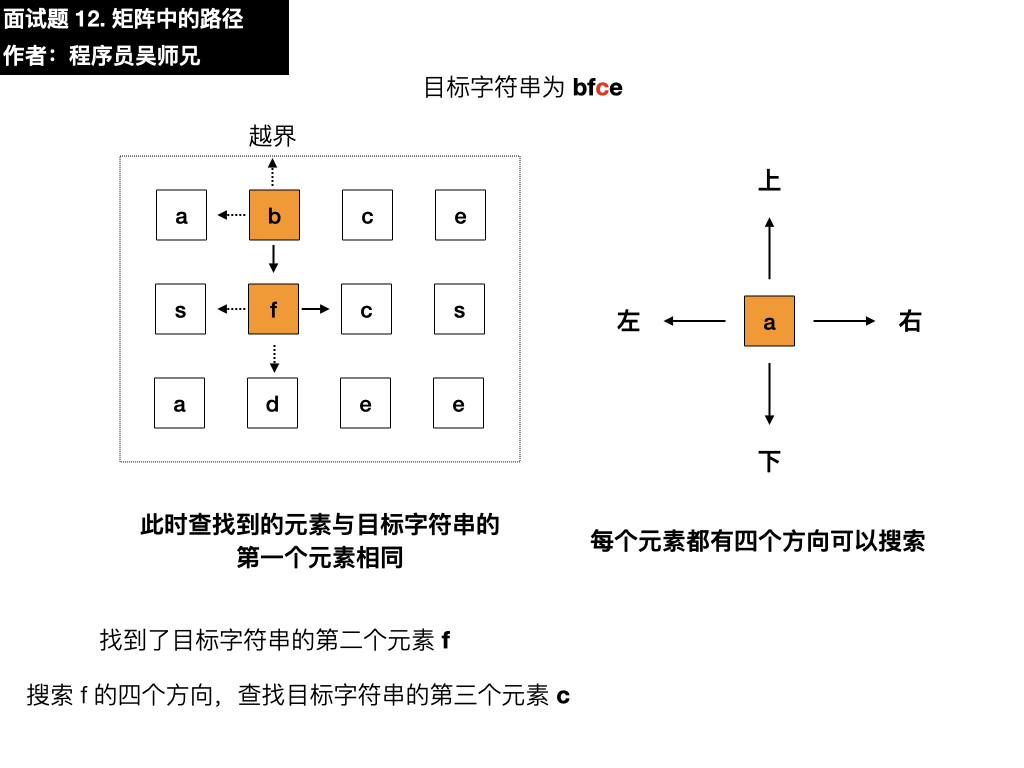
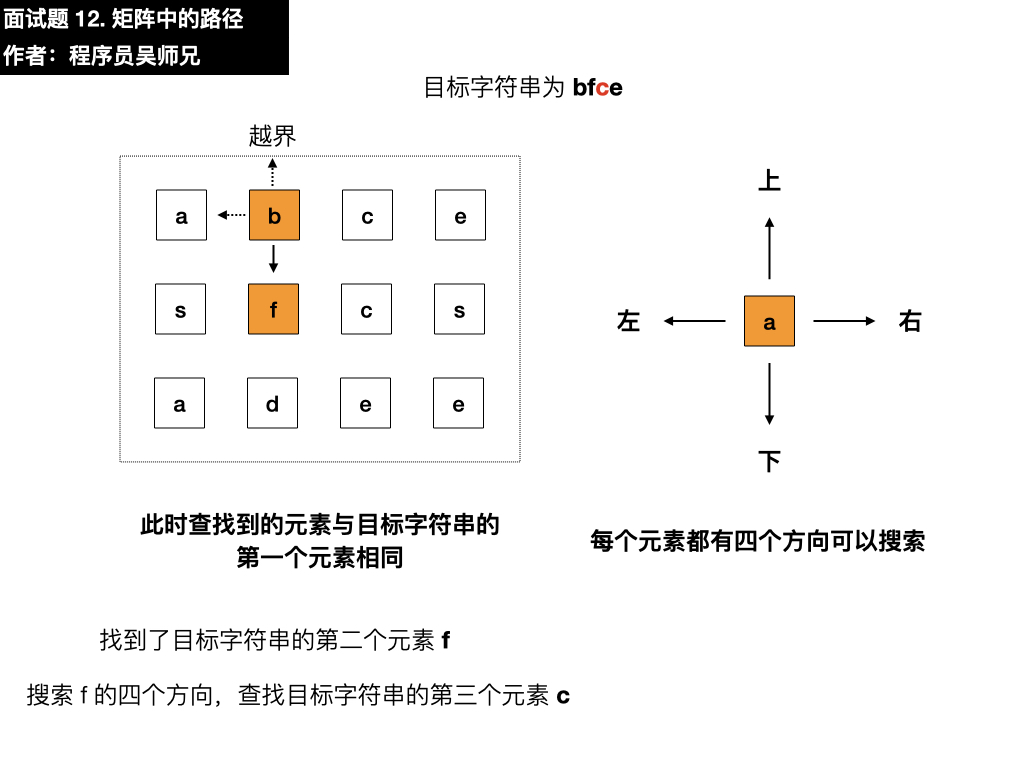
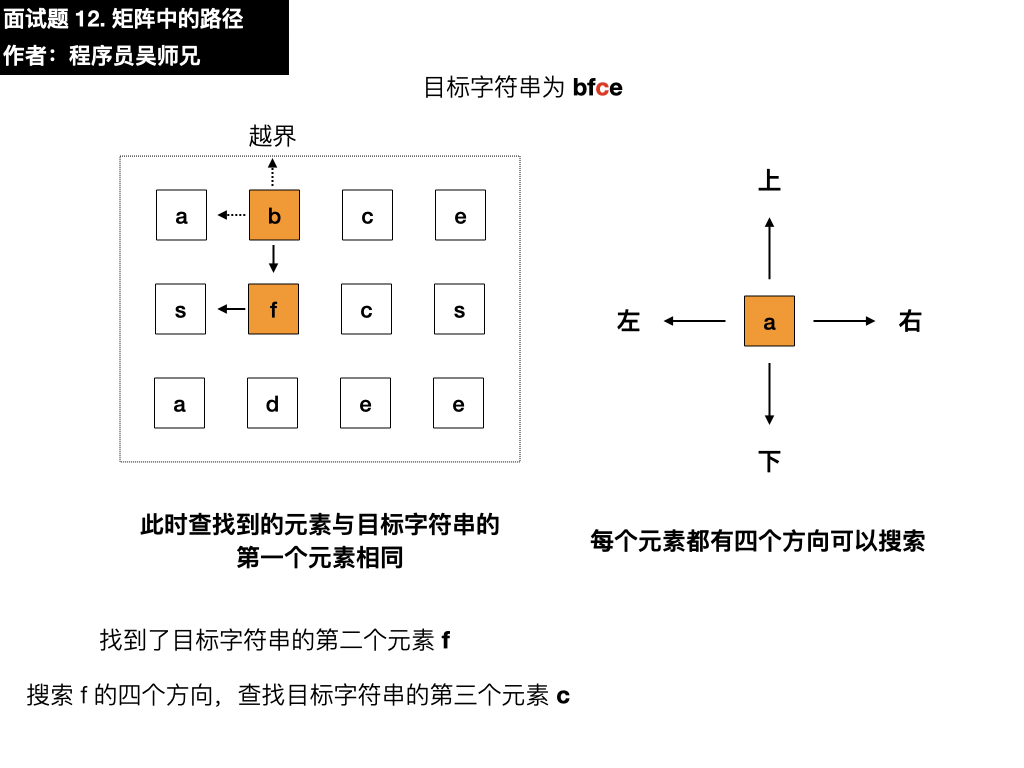
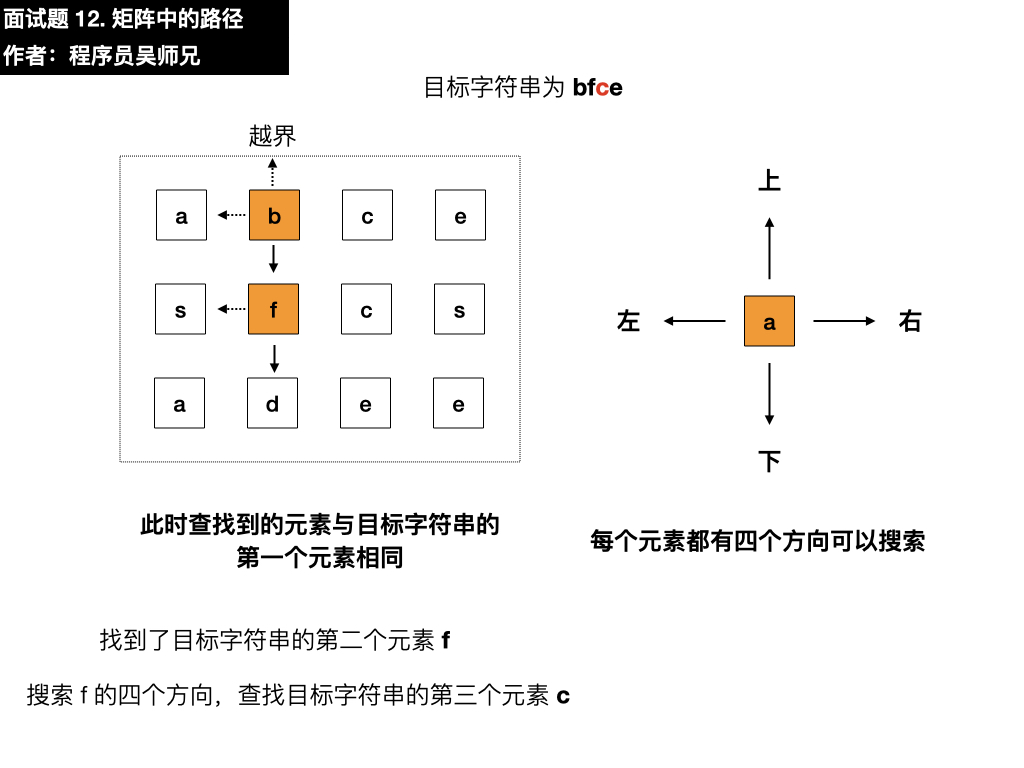
- 上:根据题目要求不需要考虑
- 左:是 s,与目标元素 c 不相同
- 下:是 d,与目标元素 c 不相同
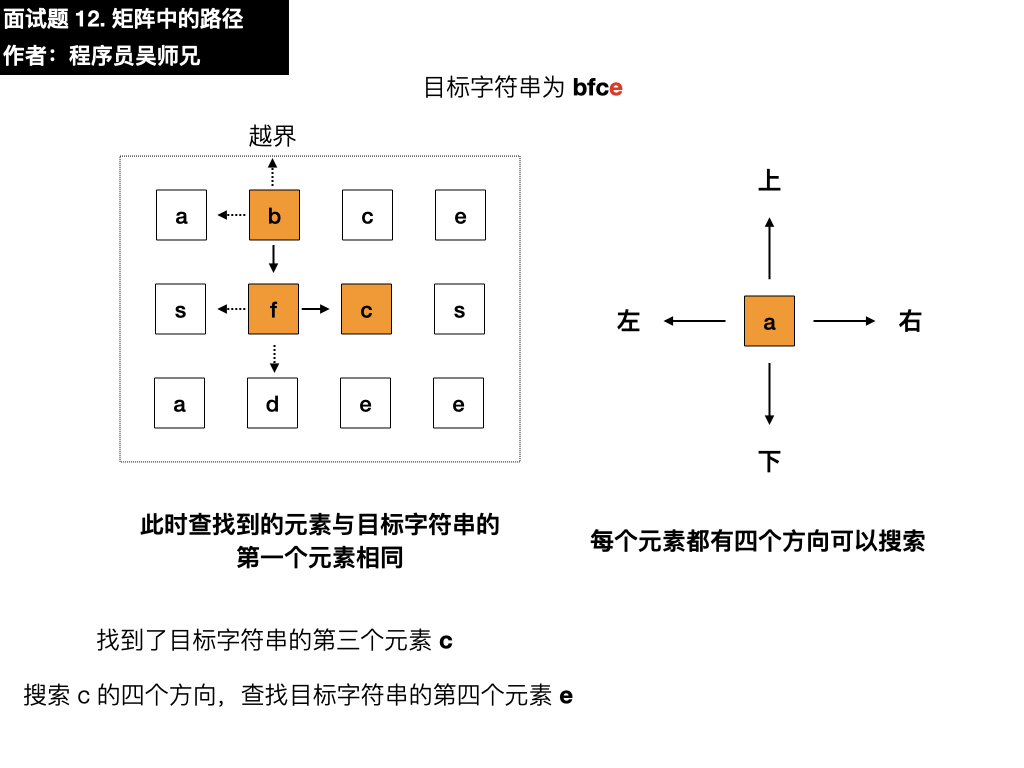
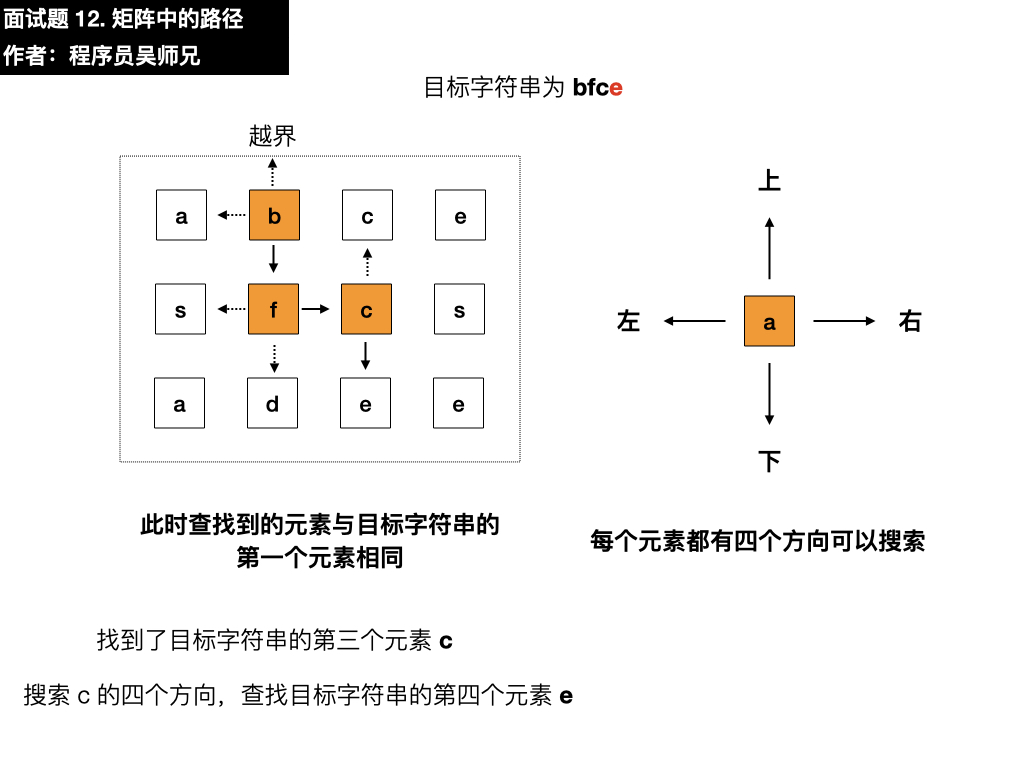
- 右:是 c,与目标元素 c 相同,符合要求,依葫芦画瓢找第四个元素
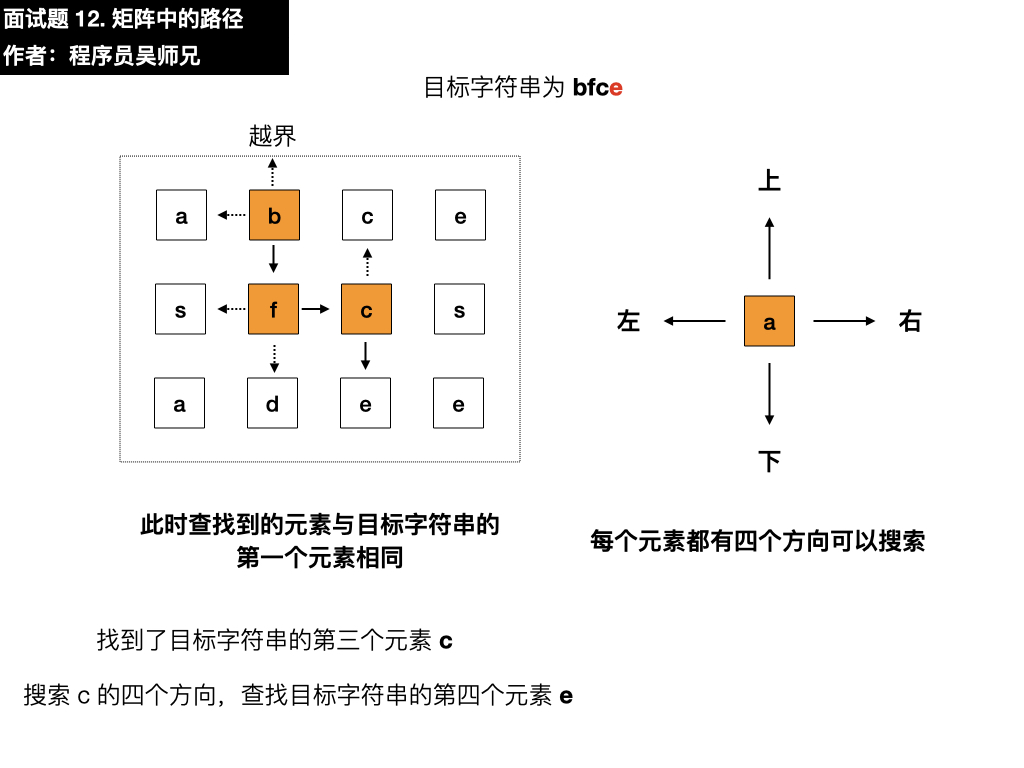
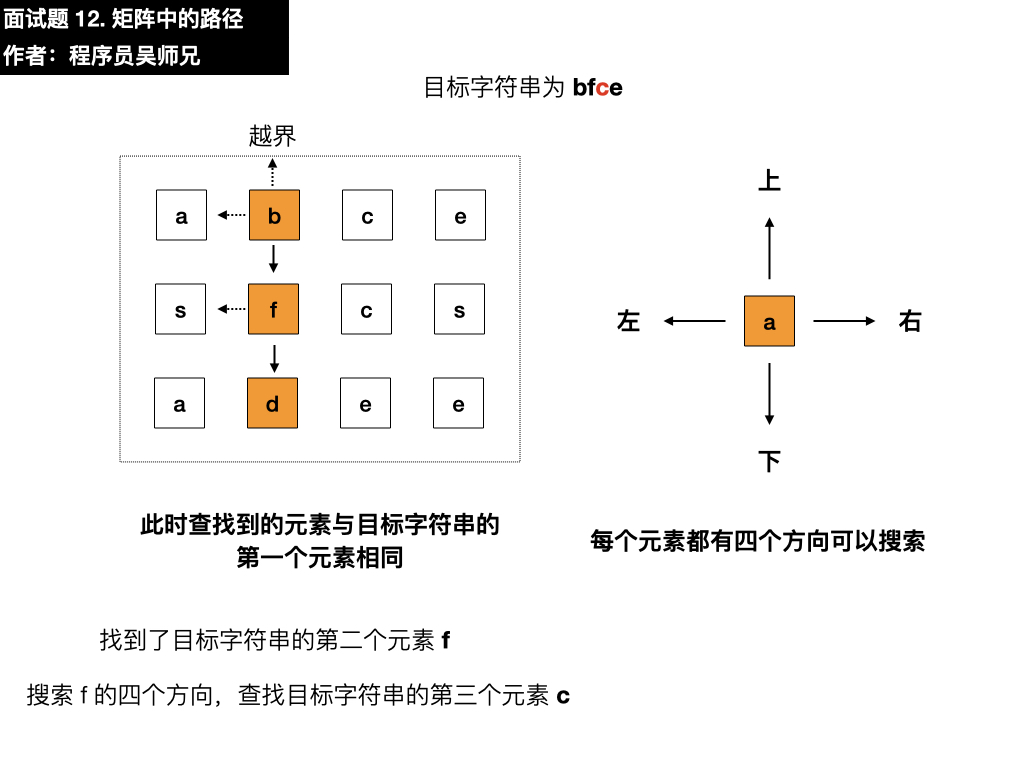
- 上:是 c,与目标元素 e 不相同
- 左:根据题目要求不需要考虑
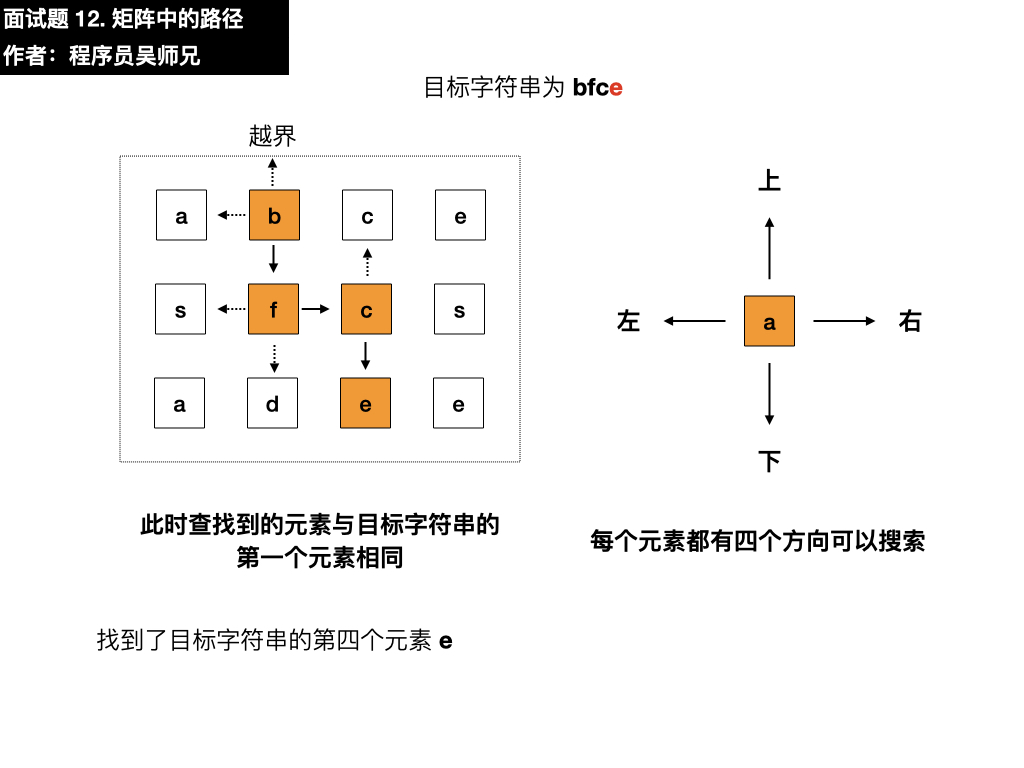
- 下:是 e,与目标元素 e 相同,符合要求,寻找结束,匹配成功,返回 true
2、规律
- 1、在搜索过程中,如果当前元素与目标元素不匹配,则回退到之前的节点再搜索
- 2、在搜索过程中,如果当前元素与目标元素相匹配,则按照上左下右的方向进行再次搜索匹配剩下的元素
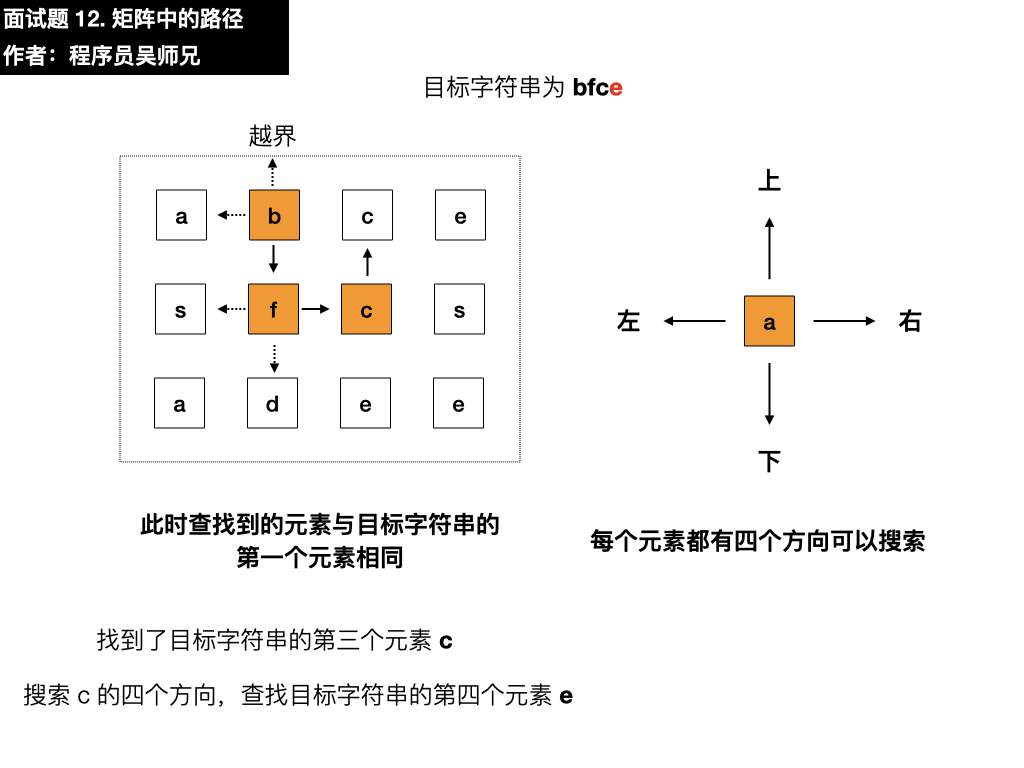
- 3、在搜索过程中,搜索当前元素的上左下右方向的元素时,会出现重复访问之前元素的情况,比如搜索匹配成功的第三个元素 c 的四个方向时,会重复访问一下 f。
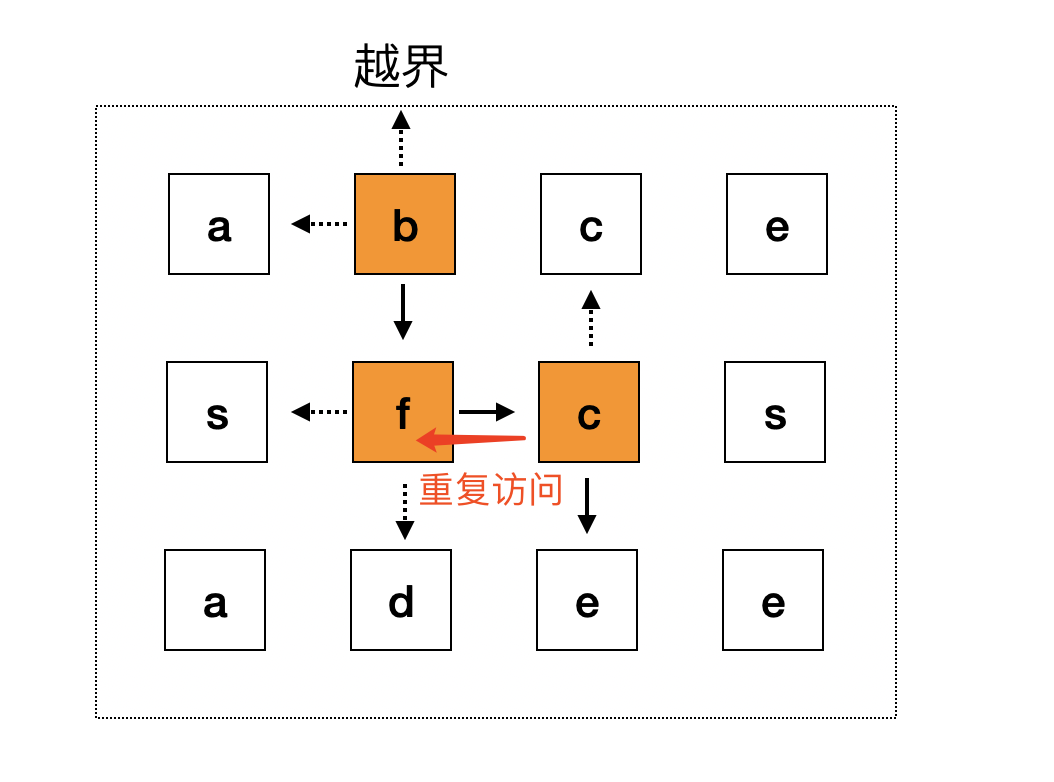
为了保证不重复访问节点,可以将这条路径上已经访问过的节点,修改为不在 word 当中的一个字符,保证以后再次访问时不会重复访问,这里我们将其修改为特殊字符 # 。
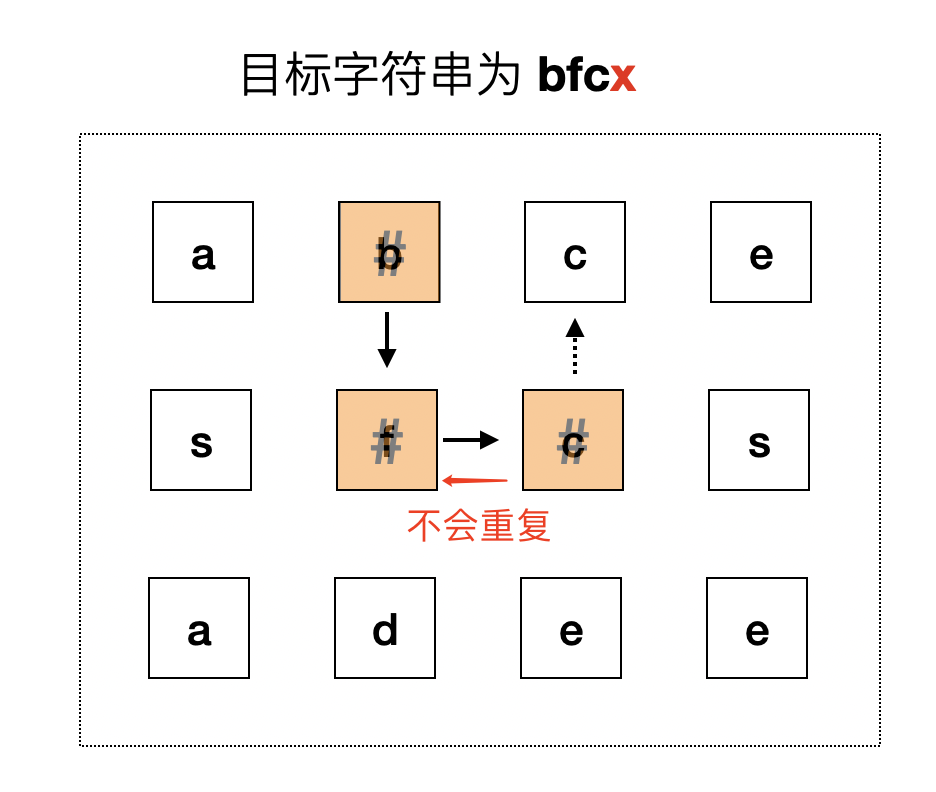
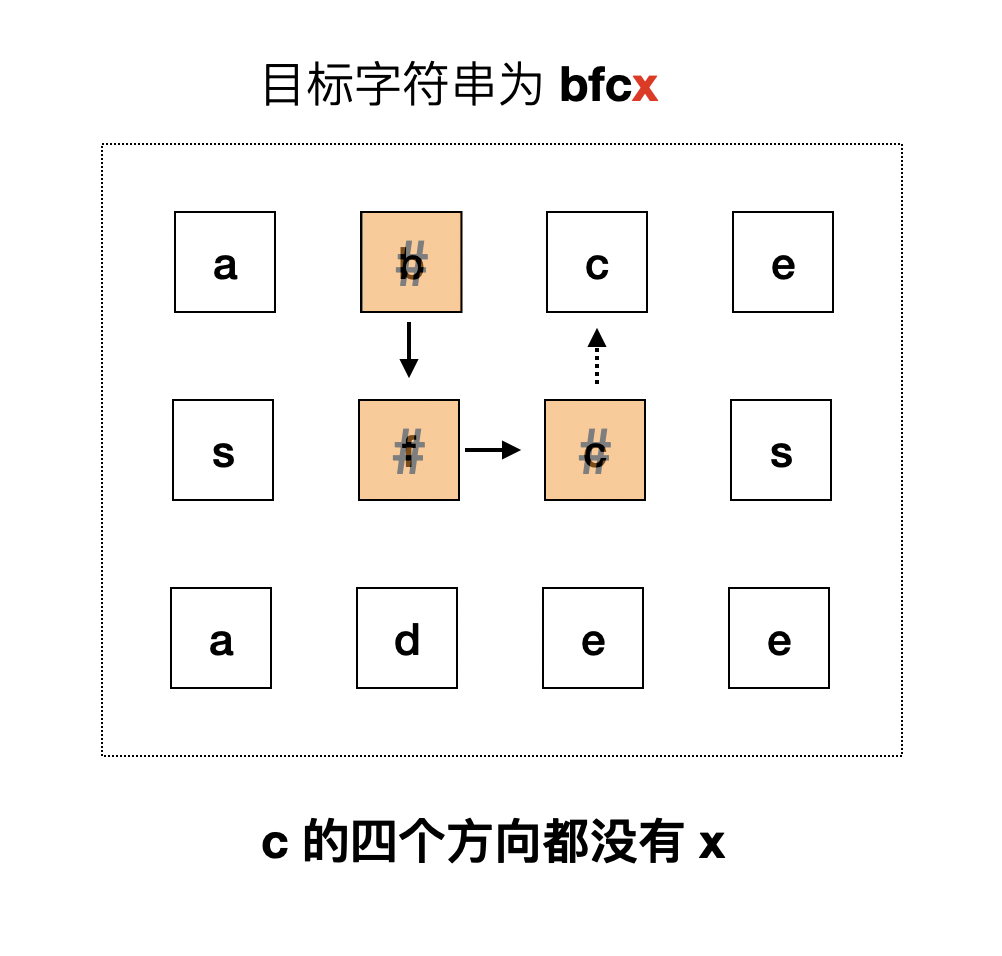
修改完后会出现一种情况,当前的节点元素与目标元素相匹配,但是在它的四个方向的节点中都找不到可以匹配到目标下一元素的节点。
比如此时当前元素 c 与目标元素 c 相匹配,但是目标下一元素为 x,而在当前元素的四个方向上都找不到 x ,需要把这个点回退,根据之前的操作,当前的节点被修改为了 #,所以为了能够回退成功,再回退操作时需要重新将 # 修改回原来的元素。
3、匹配
本题提供了一个矩阵,矩阵是一个二维数组,需要我们在二维数组中进行搜索,为了能够覆盖所有的情况,必然要使用两个嵌套的循环。
在搜索过程中,当遇到匹配成功的元素,搜索其下一元素的操作与当前的操作一致,即可以使用递归。
-
递归参数: 当前元素在矩阵
board中的行列索引i和j,当前目标字符在word中的索引k。 -
终止条件:
-
返回 false:
(1) 行或列索引越界
(2) 当前矩阵元素与目标字符不同
(3) 当前矩阵元素已访问过
-
返回 true:
k = len(word) - 1,即字符串word已全部匹配。
-
-
递推工作:
- 标记当前矩阵元素: 将
board[ i ] [ j ]修改为特殊字符 # ,代表此元素已访问过,防止之后搜索时重复访问。 - 搜索下一节点: 朝当前元素的 上、左、下、右 四个方向开启下层递归。
- 回退时还原当前矩阵元素: 将
board[ i ] [ j ]元素还原至初始值,即 word[k] 。
- 标记当前矩阵元素: 将
-
返回值: 返回布尔量
res,代表是否搜索到目标字符串。
4、边界
- 1、行越界
- 2、列越界
- 3、矩阵元素已访问过
三、动画描述
点击下方链接进行查看
https://www.algomooc.com/263.html
四、图片描述




五、参考代码
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
class Solution {
public boolean exist(char[][] board, String word) {
// 先将字符串进行拆分,一个一个元素进行匹配
char[] words = word.toCharArray();
// 通过两层嵌套,覆盖所有的情况
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
// 以该元素为起始点,递归检查是否符合要求
if(dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
// 边界情况判断
// 行越界
// 列越界
// 矩阵元素已访问过
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
// 之前已经和目标字符串匹配成功了 length - 1 个字符,此时又匹配成功了最后一个元素,直接返回结果
if(k == word.length - 1) return true;
// 标记当前矩阵元素,将其修改为特殊字符 # ,代表此元素已访问过,防止之后搜索时重复访问。
board[i][j] = '#';
// 搜索元素的四个方向 上 左 下 右,匹配下一个目标元素
boolean res = dfs( board , word , i , j - 1 , k + 1 )
|| dfs( board , word , i - 1 , j , k + 1 )
|| dfs( board , word , i , j + 1 , k + 1 )
|| dfs( board , word , i + 1 , j , k + 1 );
// 回退时还原当前矩阵元素
board[i][j] = word[k];
// 返回结果
return res;
}
}
注意 :搜索元素的四个方向 上 左 下 右,匹配下一个目标元素时的代码不要拆分,否则会出现超出时间限制,因为这样做相当于每一个方向都进行了搜索,而事实上不需要,只需要找到一条符合要求的路径即可。
boolean up = dfs(board, word, i, j - 1, k + 1);
boolean left = dfs(board, word, i - 1, j , k + 1);
boolean down = dfs(board, word, i, j + 1, k + 1);
boolean right = dfs(board, word, i + 1, j , k + 1);
boolean res = up || left || down || right;

六、复杂度分析
时间复杂度
时间复杂为 O( 4k M N ),其中 M,N 分别为矩阵行列长度, K 为字符串 word 的长度,每个字符都有 4 个方向。
空间复杂度
空间复杂度为 O(K) 。
七、相关标签
- 深度优先搜索
- 递归
- 数组
- 回溯
八、参考阅读
2、https://leetcode-cn.com/problems/ju-zhen-zhong-de-lu-jing-lcof/