题目描述
一条单向的铁路线上,依次有编号为 1, 2, …, n1,2,…,n 的 nn 个火车站。每个火车站都有一个级别,最低为 11 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 xx ,则始发站、终点站之间所有级别大于等于火车站 xx 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是 55 趟车次的运行情况。其中,前 44 趟车次均满足要求,而第 55 趟车次由于停靠了 33 号火车站( 22级)却未停靠途经的 66 号火车站(亦为 22 级)而不满足要求。
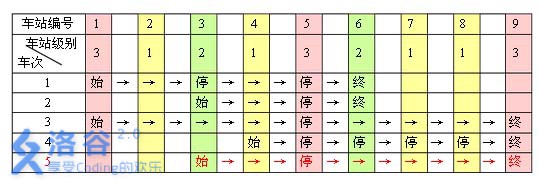
现有 mm 趟车次的运行情况(全部满足要求),试推算这 nn 个火车站至少分为几个不同的级别。
输入输出格式
输入格式:
第一行包含 22 个正整数 n, mn,m ,用一个空格隔开。
第 i + 1i+1 行 (1 ≤ i ≤ m)(1≤i≤m) 中,首先是一个正整数 s_i(2 ≤ s_i ≤ n)si(2≤si≤n) ,表示第 ii 趟车次有 s_isi 个停靠站;接下来有 s_isi个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式:
一个正整数,即 nn 个火车站最少划分的级别数。
输入输出样例
说明
对于 20\%20% 的数据, 1 ≤ n, m ≤ 101≤n,m≤10 ;
对于 50\%50% 的数据, 1 ≤ n, m ≤ 1001≤n,m≤100 ;
对于 100\%100% 的数据, 1 ≤ n, m ≤ 10001≤n,m≤1000 。
Solution:
本题经典的拓扑序DP,关键是建图卡时,需要线段树优化建图。
首先由每次的停车情况可以确定出那些没有停车的点的等级一定小于停车了的点的等级,于是从没有停车的点向停车的点连边。
然后可以确定出一张图,在图上跑拓扑序,顺便就能递推出每个点的等级了。
问题是建图时最坏是$n^3$的复杂度,但是我们发现每个点总是一段连续的点连向它。
于是想到用线段树优化建图,这东西比较神奇,一般长这样:
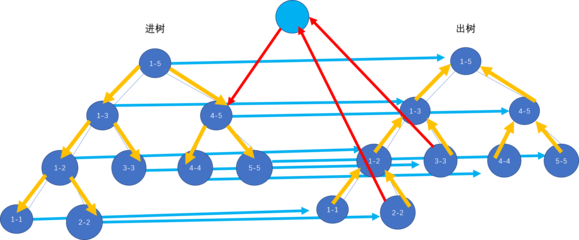
其实比较简单,就是在建树的时候维护一下子节点和父节点的边关系(注意两棵树边的方向不同),然后每次建图直接由一棵树的区间向一个虚点连边,再由该虚点向另一棵树的某一区间连边,具体实现视情况而定。
本题的话是一段区间连向一个点,于是我们只要建一棵子节点连向父节点的线段树就够了,然后就每次都多建一个虚点(不能只用一个,否则边的直接相连关系会混乱),一段区间向虚点连边,再由虚点向所连点对应的叶子节点连边。
最后就只需要跑一遍拓扑序,非叶子节点就直接由到达它的点更新,而叶子节点层数+1,处理出每个叶子节点最大的层数就是最少要的等级了。
注意实现的细节比较多。
代码:
#include<bits/stdc++.h> #define il inline #define ll long long #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) #define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--) using namespace std; const int N=1505; int h[N<<3],to[N*700],net[N*700],cnt,n,m,tp,stp[N],rd[N<<3],ar[N],f[N<<3]; bool nd[N<<3]; queue<int>q; il int gi(){ int a=0;char x=getchar(); while(x<'0'||x>'9')x=getchar(); while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return a; } il void add(int u,int v){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,rd[v]++;} il void build(int l,int r,int rt){ tp=max(tp,rt); if(l==r){ar[l]=rt,nd[rt]=1;return;} int m=l+r>>1; add(rt<<1,rt),build(lson); add(rt<<1|1,rt),build(rson); } il void update(int L,int R,int l,int r,int rt){ if(L>R)return; if(L<=l&&R>=r){add(rt,tp);return;} int m=l+r>>1; if(L<=m) update(L,R,lson); if(R>m) update(L,R,rson); } il void bfs(){ For(i,1,tp) if(!rd[i]) q.push(i),f[i]=nd[i]; while(!q.empty()){ int u=q.front();q.pop(); for(int i=h[u];i;i=net[i]){ rd[to[i]]--; f[to[i]]=max(f[u]+nd[to[i]],f[to[i]]); if(!rd[to[i]]) q.push(to[i]); } } } int main(){ n=gi(),m=gi(); build(1,n,1); int tot,ans=0; while(m--){ tot=gi();tp++; For(i,1,tot) stp[i]=gi(); For(i,1,tot-1) add(tp,ar[stp[i]]),update(stp[i]+1,stp[i+1]-1,1,n,1); add(tp,ar[stp[tot]]); } bfs(); For(i,1,n) ans=max(ans,f[ar[i]]); cout<<ans; return 0; }