UVA11294 Wedding

题目描述

PDF

输入输出格式

输入格式：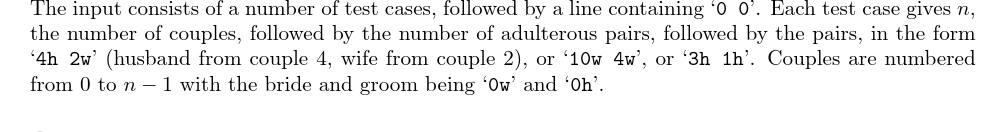

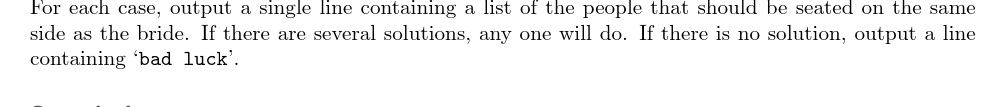
输出格式：

输入输出样例

输入样例#1：

10 6
3h 7h
5w 3w
7h 6w
8w 3w
7h 3w
2w 5h
0 0

输出样例#1：

1h 2h 3w 4h 5h 6h 7h 8h 9h

Solution：

　　本题2-SAT模板，建图细节还是蛮多的。

　　2-SAT简单来讲，就是对于每个元素只有真假两种情况，然后对于给定的二元约束方程组（约束条件比如：$x=1||y=0$），求解满足条件的解。

　　很显然可以爆搜，$O(2^n)$爆炸。

　　而2-SAT的就是在$dfs$基础上，保持不回溯，这样的最坏复杂度是$O(nm)$（即每个点都要遍历$m$条边）。

　　那么具体实现时，将点$i$拆为$2*i$和$2*i+1$两点，分别表示$i$为真或$i$为否。然后建边则需要推导，对于$i=1||j=1$此类约束条件，不难想到，需要连边$2*i+1 ightarrow 2*j$（表示的是当$i$为假时，则为满足条件必须使$j$为真），同理还需建边$2*j+1 ightarrow 2*i$（对称性建边）。接下来对于没有被标记的点逐一考虑，先假设$i$它为真，然后标记节点$2*i$，并沿着有向边标记所有能标记的节点。如果标记过程中发现某个变量对应的两个节点都被标记了，则$i$为真不成立，直接清除刚才的标记（非回溯，用栈维护dfs序实现），然后再假设$i$为假，标记$2*i+1$，继续过程。若两次标记都行不通，说明无解。

　　回到本题，我们不难发现以下约束条件：

　　　　1、当$ih,jh$冲突时，则$ih,jw$在$0w$边或者$jh,iw$在$0w$边，等价于$ih=1||jw=1$，直接建边$2*i ightarrow 2*j+1$和边$2*j ightarrow 2*i+1$。

　　　　2、当$ih,jw$冲突时，则$ih,jh$在$0w$边或者$iw,jw$在$0w$边，等价于$ih=jh$，直接建边$2*i ightarrow 2*j$和$2*j+1 ightarrow 2*i+1$。

　　那么建好边后，将$0$染为$1$，跑一下2-SAT，判断有无解，有解就判断一下染色的位置输出就好了。

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=100005;
int n,m,to[N],h[200],net[N],cnt,col[200],stk[2000],tot;

il void add(int u,int v) {to[++cnt]=v,net[cnt]=h[u],h[u]=cnt;}

il bool dfs(int u){
    if(col[u^1]) return 0;
    if(col[u]) return 1;
    col[u]=1;
    stk[++tot]=u;
    for(int i=h[u];i;i=net[i])
        if(!dfs(to[i]))return 0;
    return 1;
}

il bool check(){
    col[0]=1;
    if(!dfs(0))return 0;
    For(i,1,n-1) {
        if(col[i<<1]||col[i<<1|1])continue;
        tot=0;
        if(!dfs(i<<1)){
            while(tot) col[stk[tot--]]=0;
            if(!dfs(i<<1|1)) return 0;
        }
    }
    return 1;
}

int main(){
    char a[2],b[2];
    int la,lb,x,y;
    while(scanf("%d%d",&n,&m)==2){
        if((!n)&&(!m))break;
        cnt=0,memset(h,0,sizeof(h)),memset(col,0,sizeof(col));
        while(m--){
            scanf("%d%s%d%s",&x,a,&y,b);
            la=(a[0]=='h'?0:1),lb=(b[0]=='h'?0:1),
            add((x<<1)+la,(y<<1|1)-lb),add((y<<1)+lb,(x<<1|1)-la);
        }
        if(!check()) puts("bad luck");
        else {
            For(i,1,n-1) 
                if(col[i<<1|1]) printf("%dh ",i);
                else printf("%dw ",i);
                printf("
");
            }
    }
    return 0;    
}