P2165 [AHOI2009]飞行棋

题目描述

给出圆周上的若干个点，已知点与点之间的弧长，其值均为正整数，并依圆周顺序排列。 请找出这些点中有没有可以围成矩形的，并希望在最短时间内找出所有不重复矩形。

输入输出格式

输入格式：

第一行为正整数N，表示点的个数，接下来N行分别为这N个点所分割的各个圆弧长度

输出格式：

所构成不重复矩形的个数

输入输出样例

输入样例#1： 

8
1
2
2
3
1
1
3
3

输出样例#1： 

3

说明

N<=20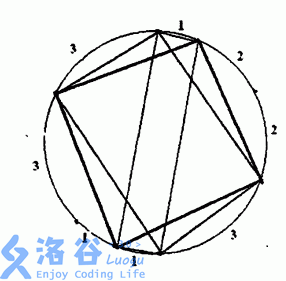

Solution:

　　本题看似很水（确实很水），自己的想法却不够简便。

　　开始写了个暴力枚举$4$个点然后判断，老是处理不了重复的情况搞了半天一直$40$分。

　　其实，我们只需要处理出前缀和，然后$n^2$枚举$i,j$，当$s[j]-s[i]==s[n]/2$时，计数器$ans++$，因为我们知道矩形的两条邻边所成的圆周角$=pi$，所以弧长为$frac{c}{2}$（$c$为圆的周长），于是我们这样统计出来的是满足条件的成对角的点对个数，那么最后的答案就是$ans*(ans-1)/2$（简单的组合，每个点对可以和剩下$ans-1$个点对搭配组成矩形，然后每个会重复算一次，所以除以$2$就$OK$了）。

代码：

#include<bits/stdc++.h>
#define il inline
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
using namespace std;
const int N=100;
int n,a[N],s[N],ans;
il void solve(){
    For(i,1,n) For(j,1,n)if(s[j]-s[i]==s[n]/2)ans++;
    cout<<ans*(ans-1)/2;
}
int main(){
    ios::sync_with_stdio(0);
    cin>>n;
    For(i,1,n)cin>>a[i];
    For(i,1,n)s[i]=s[i-1]+a[i];
    solve();
    return 0;
}