理解题意后分两种情况:
1.b在a的上方: min(dep[p]-1,k)*(ll)siz[p] 因为(p点上方肯定有父亲结点b,我们不用管b是谁)
2.b在a的下方: (dep(p)+1 ~ dep(p)+k矩形框内的所有点子树个数和
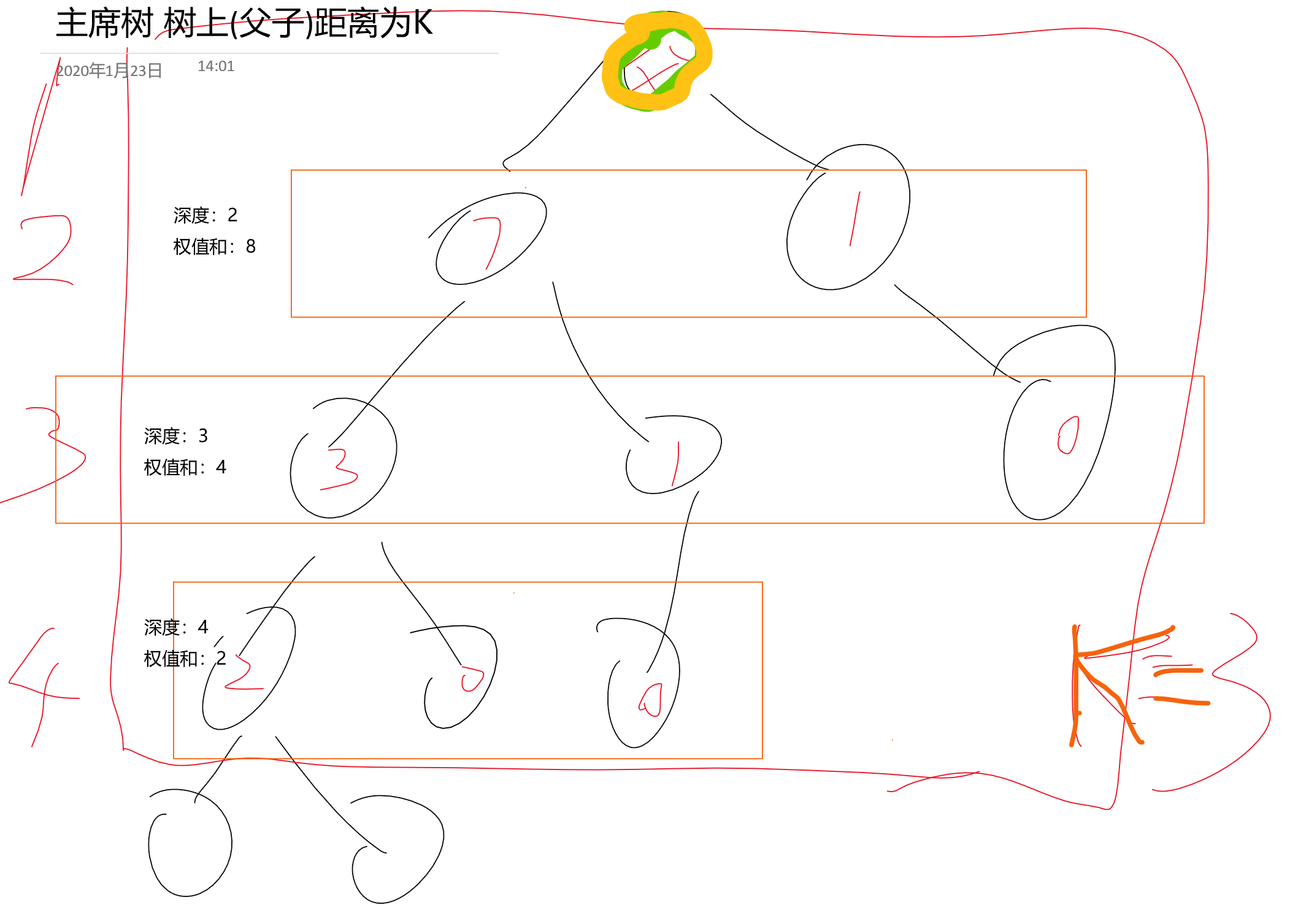
所以思路:主席树维护同一深度下的各个结点子树个数和;下标是深度,权值维护的是子树个数和;在dfs序in和out时间戳上建立主席树,把树上问题转变为区间序列问题,利用dfs序时间戳的性质(子树编号在入时间戳和出时间戳的区间内),查询以p为根子树;所以问题就转变为了查询时间戳内区间内距离为k的点权和(相当于查询 矩形框 框住部分的点的个数了)。用线段树维护貌似也是可以的。
灵魂画手
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,q;
const int maxn = 3e5+10;
vector<int> g[maxn];
int depth[maxn];
ll size[maxn];
int e = 0;
int in[maxn],out[maxn],root[maxn];
int ma_siz[maxn],ma_dep[maxn];
struct Node{
ll v;
int lc,rc;
}T[maxn*24];
//递归计算dfs序 size子树大小 depth深度
void dfs(int x,int fa){
in[x] = ++e;
size[x] = 1;
depth[x] = depth[fa] + 1;
for(int i=0;i<g[x].size();i++){
int v = g[x][i];
if(v != fa){
dfs(v,x);
size[x] += size[v];
}
}
out[x] = e;
}
//主席树update
void update(int pre,int cur,int pos,ll v,int l,int r){
if(l == r){
T[cur].v = T[pre].v + v;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid){
T[cur].lc = ++e;
T[cur].rc = T[pre].rc;
update(T[pre].lc,T[cur].lc,pos,v,l,mid);
}else{
T[cur].rc = ++e;
T[cur].lc = T[pre].lc;
update(T[pre].rc,T[cur].rc,pos,v,mid+1,r);
}
T[cur].v = T[T[cur].lc].v + T[T[cur].rc].v;
}
//查询区间ql~qr的权值(子树个数和) emmm是不是直接用权值线段树也是可以的啊
ll query(int pre,int cur,int ql,int qr,int l,int r){
if(ql <= l && r <= qr){
return T[cur].v - T[pre].v;
}
int mid = (l + r) >> 1;
ll res = 0;
if(ql <= mid) res += query(T[pre].lc,T[cur].lc,ql,qr,l,mid);
if(qr > mid) res += query(T[pre].rc,T[cur].rc,ql,qr,mid+1,r);
return res;
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>q;
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,1);
for(int i=1;i<=n;i++){
size[i]--;
ma_siz[in[i]] = size[i]; //新序号-dfs序上的权值:子树个数
ma_dep[in[i]] = depth[i]; //新序号-dfs序上的下标:所在位置为深度dep
}
for(int i=1;i<=n;i++){
root[i] = ++e;
update(root[i-1],root[i],ma_dep[i],ma_siz[i],1,n);
}
while(q--){
int p,k;
cin>>p>>k;
cout<<(ll)min(depth[p]-1,k)*size[p] + (ll) query(root[in[p]],root[out[p]],depth[p]+1,min(depth[p]+k,n),1,n)<<endl;
}
return 0;
}