线段树区间更新 费马小定理|魔豆传奇

程序设计：魔豆传奇
《魔豆传奇》是2004年的一部动画片。里面有很多奇怪的魔豆，具有奇特且强大的能力。
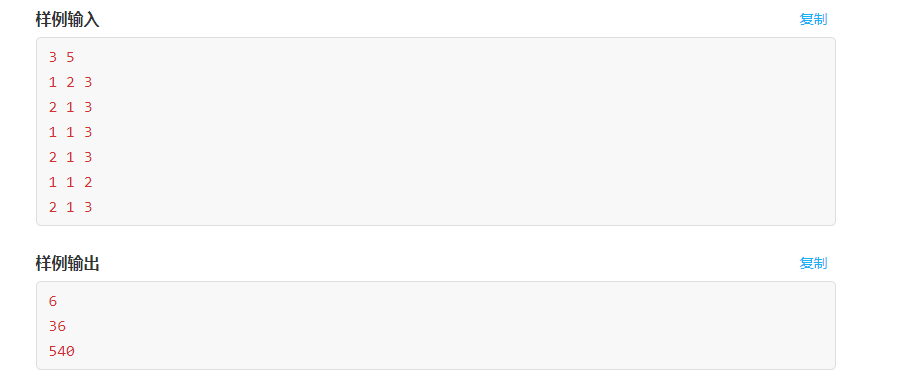
偶然间，蒜头君获得了一排已经发芽的魔豆，每株的最初高度为ai 。
蒜头君每天都会选择对一段区间的魔豆浇水，或查看一段区间魔豆的高度和。
魔豆每一次被浇水，其高度会变为之前高度的立方。
也就是说，蒜头君有两种操作：
1.使序列中下标在区间[L,R] 中的每个数变成自己的立方。
2.查询序列中下标在区间[L,R]中的数值和。
由于魔豆高度过大，查询时你需要输出数值和对1046513837 取模的结果。

题解：

线段树做法：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define LL long long
#define mod 1046513837

int n, m;
int a[100010], f[400010][30], tmp[30], lazy[400010];

//更新lazy标记 
void push(int t)
{
    if (!lazy[t]) return;
    //下放标记 
    lazy[t + t] = (lazy[t + t] + lazy[t]) % 28;
    lazy[t + t + 1] = (lazy[t + t + 1] + lazy[t]) % 28;
    //更新子区间2*t 
    for (int i = 0; i < 28; ++i) tmp[i] = f[t + t][i];
    for (int i = 0; i < 28; ++i) f[t + t][i] = tmp[(i + lazy[t]) % 28];
    //更新子区间2*t+1 
    for (int i = 0; i < 28; ++i) tmp[i] = f[t + t + 1][i];
    for (int i = 0; i < 28; ++i) f[t + t + 1][i] = tmp[(i + lazy[t]) % 28];
    lazy[t]=0;
}

void build(int t, int l, int r)
{
    if (l == r)
    {
        f[t][0] = a[l];//初始值 就是a数组的值 
        for (int i = 1; i < 28; ++i)
        {
            f[t][i] = (LL)f[t][i - 1] * f[t][i - 1] % mod * f[t][i - 1] % mod; //f数组第二维 表示第i个3次方  可以从0个3次方初始值递推 
        }
        return;
    }
    int mid = (l + r) / 2;
    build(t + t, l, mid);
    build(t + t + 1, mid + 1, r);
    for (int i = 0; i < 28; ++i) f[t][i] = (f[t + t][i] + f[t + t + 1][i]) % mod; //当前区间f数组 f[t][i]等于 两个子区间的和 
}

//更新 
void modify(int t, int l, int r, int x, int y)
{
    if (x <= l && r <= y)
    {
        lazy[t] = (lazy[t] + 1) % 28;
        for(int i = 0; i < 28; ++i) tmp[i] = f[t][i];
        for(int i = 0; i < 28; ++i) f[t][i] = tmp[(i + 1) % 28];
        return;
    }
    push(t);
    int mid = (l + r) / 2, res = 0;
    if (x <= mid) modify(t + t, l, mid, x, y);
    if (y > mid) modify(t + t + 1, mid + 1, r, x, y);
    for(int i = 0; i < 28; ++i) f[t][i] = (f[t + t][i] + f[t + t + 1][i]) % mod;
}

int sum(int t, int l, int r, int x, int y)
{
    if (x <= l && r <= y) return f[t][0];
    push(t);//求t结点时 下放更新 t的值 
    int mid = (l + r) / 2, res = 0;
    if (x <= mid) res += sum(t + t, l, mid, x, y);
    if (y > mid) res += sum(t + t + 1, mid + 1, r, x, y);
    for (int i = 0; i < 28; ++i) f[t][i] = (f[t + t][i] + f[t + t + 1][i]) % mod;
    return res % mod;
}

int main()
{
    memset(lazy, 0, sizeof(lazy));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    build(1, 1, n);
    for (int i = 1; i <= m; ++i)
    {
        int o, l, r;
        scanf("%d%d%d", &o, &l, &r);
        if (o == 2) printf("%d
", sum(1, 1, n, l, r));
        else modify(1, 1, n, l, r);
    }
    return 0;
}