三角数字
Q: 什么是三角数字?
A: 据说一群在毕达哥拉斯领导下工作的古希腊的数学家,发现了在数学序列1,3,6,10,15,21,……中有一种奇特的联系。这个数列中的第N项是由第N-1项加N得到的。
由此,第二项是由第一项(1)加上2,得3。第三项是由第二项(3)加上3得到6,依次类推。
这个序列中的数字被称为三角数字,因为它们可以被形象化地表示成对象的一个三角形排列。 
Q: 如何使用循环求第N项?
A: 示例:TriangleNumber.java
Q: 如何使用递归求第N项?
A: 导致递归的方法直接返回而没有再一次进行递归调用,此时我们称为基值情况(base case)。
A: 每一个递归方法都有一个基值(中止)条件,以防止无限地递归下来,避免由此引发的程序崩溃,这一点至关重要。
A: 示例:TriangleNumber.java
Q: 到底发生了什么?
A: 通过插入一些输出语句来跟踪观察参数和返回值,示例:TriangleNumber.java
输出结果如下:
Enter a number = 5 Entering n = 5 Entering n = 4 Entering n = 3 Entering n = 2 Entering n = 1 Returning 1 Returning 3 Returning 6 Returning 10 Returning 15 Triangle = 15
A: calcN()方法调用自身时,它的形参从5开始,每次减1。这个方法反复地调用自身,直到方法的形参减少到1,于是方法返回。 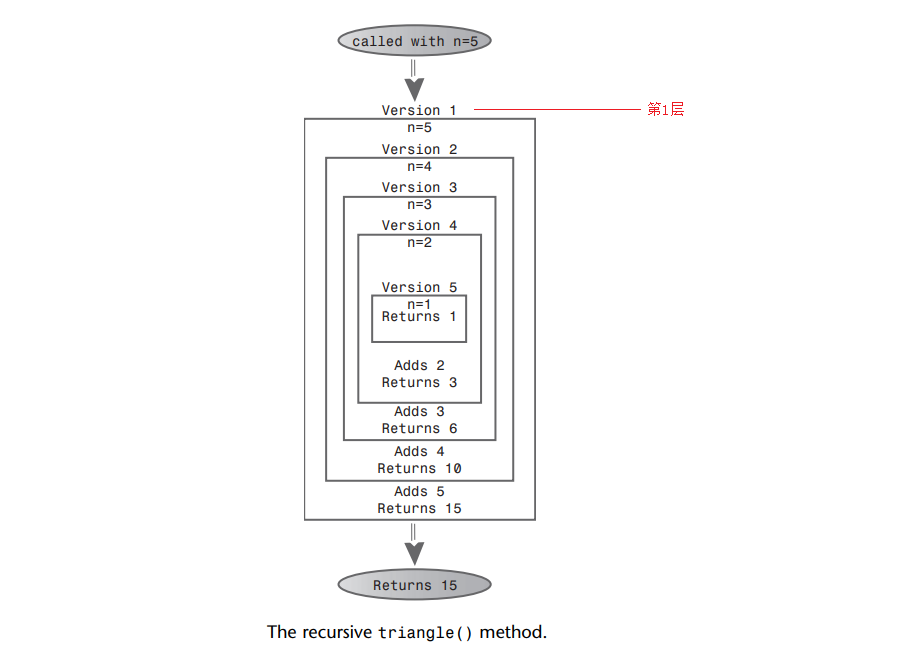
A: 这会引发一系列的返回序列,每当返回时,这方法把调用它的形参N与其调用下一层方法的返回值相加。直到结果返回给main()。
A: 返回值概括了三角数字序列。
A: 注意,在最内层返回1之前,实际上同一时刻有5个不同的calcN()方法实例存在。最外层传入的参数是5;最内层传入的参数是1。
Q: 递归方法的特征有哪些?
A: 递归算法的关键特征:
- 调用自身
- 当它调用自身的时候,它这样做是为了解决更小的问题
- 存在某个足够简单的问题的层次,在这一层算法不需要调用自己就可以直接解答,且返回结果。
Q: 递归方法是否是高效率的?
A: 调用一个方法会有一定的额外开销。控制必须从这个调用的位置转移到这个方法的开始处。除此之外,传给这个方法的参数和这个方法的返回的地址都要被压入到一个内部的栈,为的是这个方法可以访问参数值和知道返回到哪里。
A: 就calcN()这个方法来讲,因为有上述开销,可能while循环方法执行的速度比递归要快,在此示例中递归的代价也许不断太高。
A: 另外一个低效率反映在系统内存空间存储所有的中间参数以及返回值,如果有大量的数据需要存储,这就会引起栈溢出的问题。
A: 人们常常采用递归,是因为它从概念上简化了问题,而不是因为它本质上更有效率。
最大公约数
Q: 如何求两个正整数的最大公约数?
A: 12与16的最大公约数是4,一般记为(12,16)=4。
12、15、18的最大公约数是3,记为(12,15,18)=3。
A: 在求解最大公约数的几种方法中,辗转相除法最为出名,也叫欧几里德算法。
Q: 最大公约数的代码实现?
A: 示例:Gcd.java
变位字
Q: 什么是变位字(anagrams)?
A: 假设想要列出一个指定单词的所有变位字,也就是列出该词的全排列。我们称这个工作是变位一个单词。比如,全排列abc,会产生
abc acb bac bca cba cab
排列的数量是单词字母数的阶乘。所以算法至少时间O(n!)的。
A: 实际上,全排列算法对大型的数据是无法处理的,而一般情况下也不会要求我们去遍历一个大型数据的全排列。
A: n 个元素的全排列问题可转化为求n - 1个元素的全排列问题(递归设计)
A: 全排列的递归算法:
- 集合X中元素的全排列记为perm(X)
- (ri)perm(X) 表示在全排列 perm(X)的每一个排列前加上前缀得到的排列。
- R的全排列可归纳定义如下:
1) 当 n = 1 时,perm(R) = (r),其中 r 是集合 R 中唯一的元素;
2) 当 n > 1 时,perm(R) 由 (r1)perm(R1),(r2)perm(R2),…,(rn)perm(Rn)构成。
Q: 变位字的代码实现?
A: 示例:AnagramTestCase.java

递归的二分查找
Q: 如何用递归取代循环?
A: 在前面第2章"数组"中讨论过的二分查找,当时使用的是基于循环的方法来实现,现在可以改为使用递归的方法来实现。
A: 在递归的方法中,不用改变left或者right,而用left或者right的新值作为参数反复调用recFind()方法,它每一次调用自己都比上一次的范围更小。
A: 当最内层的方法找到了指定的数据项,方法返回这个数据项所在数组的下标。于是这个值依次从每一层recFind()中返回,最后,find()返回值给类用户。可以把示例中的DEBUG开关打开仔细观察,如下图。 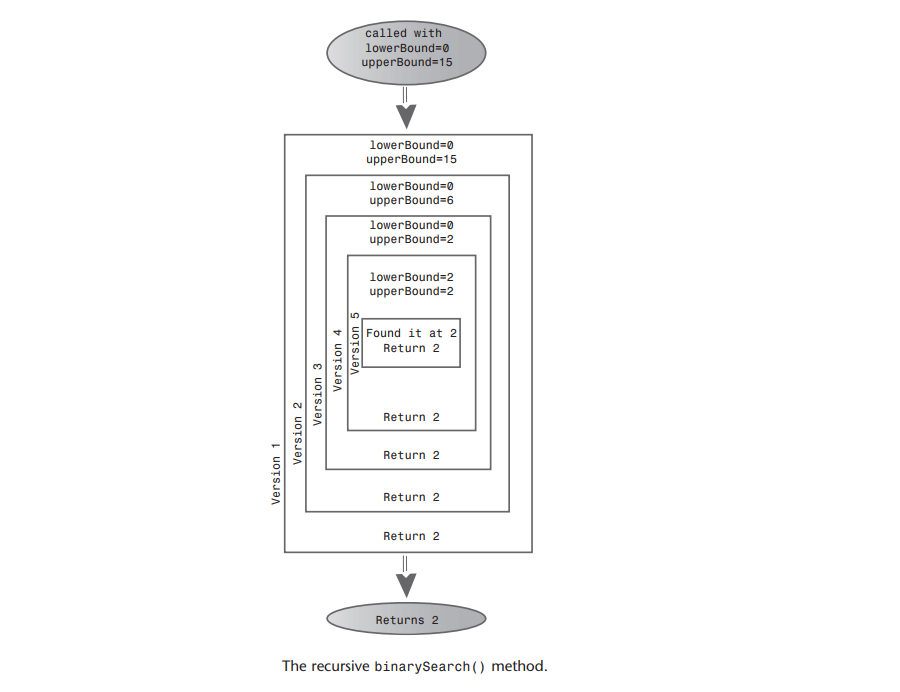
A: 递归的方法和循环的方法有同样的大O效率:O(logN)。递归的二分查找在代码量上更为简洁,但是它的速度可能会慢一些。
Q: 什么是分治算法?
A: 凡治众如治寡,分数是也。 —《孙子兵法》
大概意思就是:治理大军团就象治理小部队一样有效,是依靠合理的组织、结构、编制。
A: 将一个难以直接解决的大问题,合理分割成一些规模较小的相同问题,以便各个击破,这个策略就叫分而治之(分治法)。
A: 递归的二分查找是分治算法的一个例子。把一个大问题分成两个相对来说更小的问题,并且分别解决每一个小问题。对每一个小问题的解决方法是一样的:把每个小问题分成两个更小的问题,并且解决它们。这个过程一直持续下去直到易于求解的基值情况,就不用再继续分了。
A: 分治算法通常要回到递归。
汉诺(Hanoi)塔问题
Q: 汉诺塔问题?
A: 用子树的概念进行递归是解决汉诺塔难题的方法。假设想要把所有的盘子从源塔座上(from)移动到目标塔座上(to),有一个可以使用的中介塔座(inter)。假定在from上有n个盘子,算法如下:
- 从from移动上面n-1个盘子的子树到inter上;
- 从from移动剩余的盘子(即最大的盘子)到塔座to上;
- 从inter移动子树到to
A: 当开始的时候,原塔座是A,中介塔座是B,目标塔座是C,如下图显示了这种情况的三个步骤。如下图, 
当然这个方法并没有解决如何把包括盘子1、2和3的子树移动到塔座B上,要想解决这个问题,我们就得使用递归的思路,按照上面的三个步骤来套:从塔座A上移动最上面的两个盘子的子树到中介塔座C上,接着从A移动盘子3到塔座B上,然后把子树从塔座C移回到塔座B上。
接下来就是如何把两个盘子的子树从塔座A上移动到塔座C上呢?从塔座A上移动只有一个盘子(盘子1)的子树到塔座B上,这就是基值条件:当移动一个盘子的时候,只要移动它就可以了,没有其他的事情要做。然后从塔座A移动更大的盘子(盘子2)到塔座C,并且把这颗子树(盘子1)重新放置在这个更大的盘子上。
Q: 汉诺塔的代码实现?
A: 示例:Tower.java
归并排序
Q: 如何归并两个有序数组?
A: 在介绍归并排序算法之前,我们先看如何归并两个有序数组A和B。
A: 将两个有序表合并成一个有序表,称为二路归并。
A: 假设有两个有序数组,不要求有相同的大小。设数组A有4个元素,数组B有6个元素,它们要被归并到数组C。如下图: 
Q: 归并排序的代码实现?
A: 示例:MergeSort.java
A: 归并排序的思想是把一个数组分为两半,排序每一半,然后用merge()方法把数组的两半归并成一个有序的数组。如何来为每一部分排序呢?递归。反复地分割数组,直到得到的子数组只含有一个数据项,这就是基值条件。
A: 当初始的数组大小是2的n次幂的时候,最容易理解,如下图, 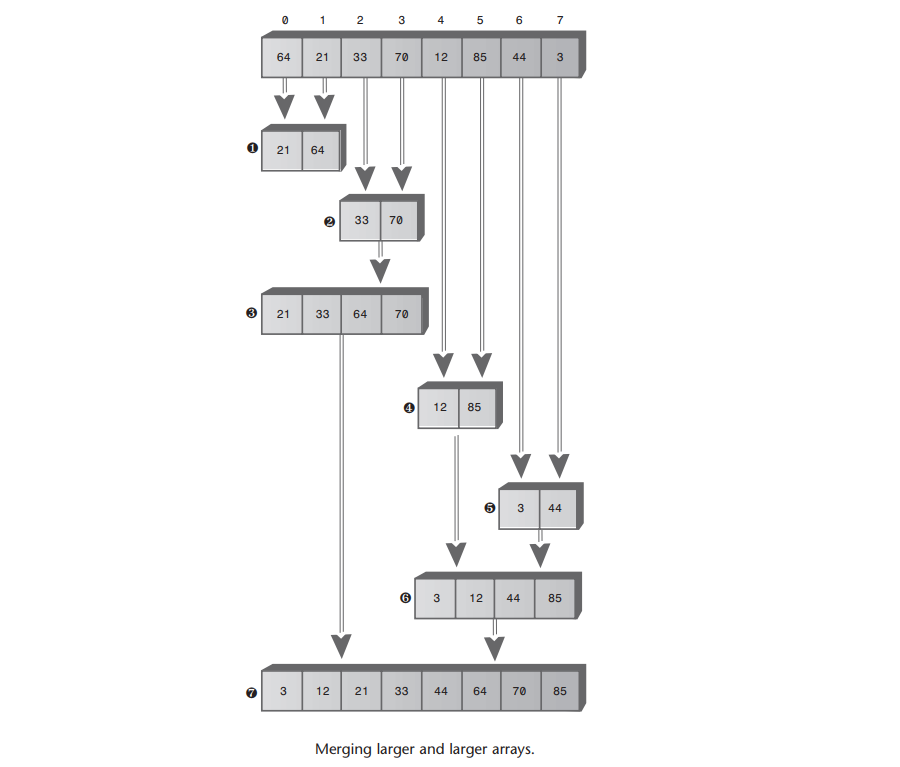
A: 当数组的大小不是2的n次幂的时候,必须要归并不同size的数组,如下图,数组的size是12的情况,这里是一个size为2的数组要和一个size为1的数组归并为一个size为3的数组。 
A: 如果把DEBUG开关打开,就可以打印如下的日志:
Entering 0 ~ 3
Will sort left half of 0 ~ 1
Entering 0 ~ 1
Will sort left half of 0 ~ 0
Entering 0 ~ 0
Base-Case Return 0 ~ 0
Will sort right half of 1 ~ 1
Entering 1 ~ 1
Base-Case Return 1 ~ 1
Will merge halves into 0 ~ 1
Return 0 ~ 1
Will sort right half of 2 ~ 3
Entering 2 ~ 3
Will sort left half of 2 ~ 2
Entering 2 ~ 2
Base-Case Return 2 ~ 2
Will sort right half of 3 ~ 3
Entering 3 ~ 3
Base-Case Return 3 ~ 3
Will merge halves into 2 ~ 3
Return 2 ~ 3
Will merge halves into 0 ~ 3
Return 0 ~ 3
与上面的图所展示的情况几乎吻合。
A: 有人可能会问,所有的这些子数组都存放在什么地方?在这个算法中,创建了一个和初始数组一样大小的工作空间数组,这些子数组就存储在这个空间数组里面,也就是说原始数组的子数组被复制到工作空间数组的相应空间上,在每一次归并之后,工作数组的内容被复制回原来的数组。
Q: 归并排序的效率?
A: 冒泡排序、插入排序和选择排序要用O(N2)时间,而归并排序只要O(N*logN)。如果N是10000,那么N2就是100000000,而N*logN只是40000。如果为这么多数据项排序用归并排序的话,需要40秒,那么插入排序则会需要将近28个小时。
A: 如何知道这个O(N*logN)时间呢?假设归并排序中复制和比较时最费时的操作,递归的调用和返回不增加额外的开销。
A: 复制的次数
考虑图(Merging larger and larger arrys)中,首行下面的每一个单元都代表从数组复制到工作空间中的一个数据项。7个标数字的步骤显示了需要有24次复制。对于有8个数据项的情况,复制的次数和O(N*logN)成正比。
实际上,这些数据项不仅被复制到数组workspace中,而且也会被复制回原数组中,这会使得复制的次数增加了一倍。下表初略地表达了这个信息。 
另一种用来看计算复制次数的方法是,排序8个数据项需要有3层,每一层包含8次复制,一层意味着所有元素都复制到相同大小的子数组中。所以就有3*8=24次复制了。
当N不是2的倍数时,比较的次数会落在2的乘方以内。对于12个数据项,总共有8次复制,并且对于100个数据项,总共有1344次复制。
A: 比较的次数
在归并排序算法中,比较的次数总是比复制的次数稍微少一些。那么少多少呢?
假设数据项的个数是2的乘方,对于每一个独立的归并操作,比较的最大次数总是比正在被归并的数据项个数少1,并且比较的最少次数是正在被归并的数据项数目的一半。
下图表明了试图归并各有4个数据项的两个数组时的两种场景,最差情况和最好情况。 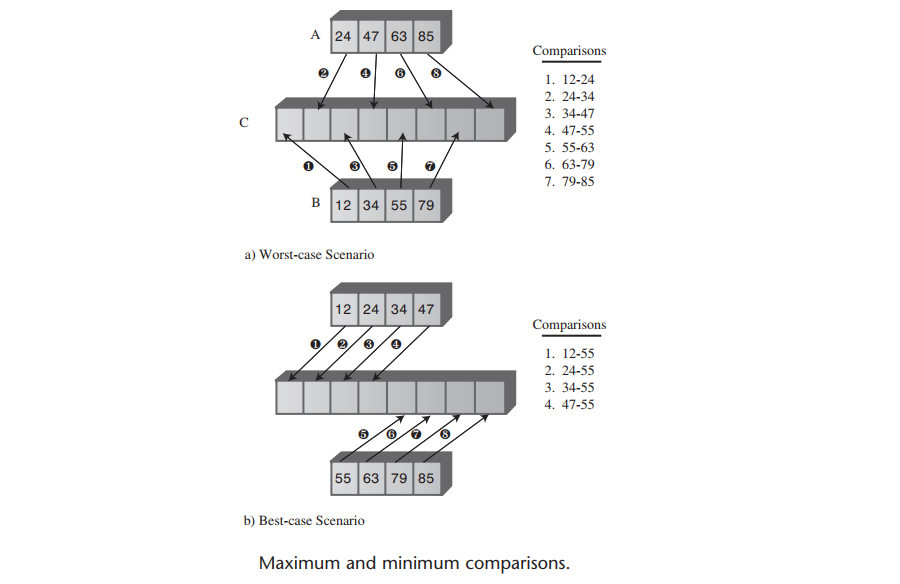
A: 重新来看图(Merging larger and larger arrys),可以看到为8个数据项进行排序,需要有7次归并操作,正在被归并的数据项个数以及相应的比较次数如下表所示, 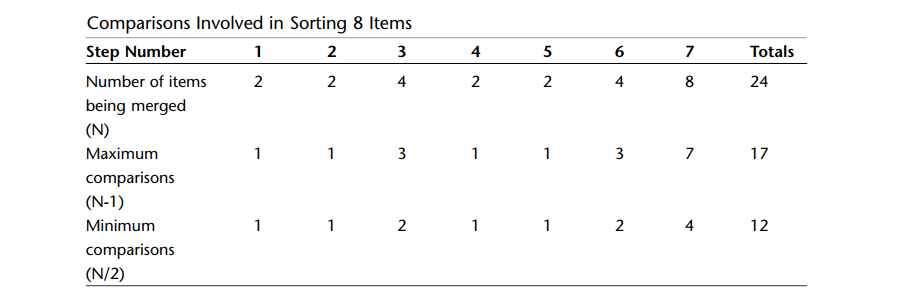
对于每一次归并,最大的比较次数比数据项的个数少一,我们把所有归并的比较次数加在一起得到总数17,最小的比较次数总是被归并的数据项个数的一半,总数为12。相似的算术运算得到如表(Number of Operations When N Is a Power Of 2)中最后一栏“比较次数栏”里。
A: 排序一个指定数组的实际比较次数依赖于数据是如何排列的,但是这个数字一定会在最大比较次数和最小比较次数之间。
消除递归
Q: 递归和栈的关系?
A: 递归和栈之间有一个紧密的联系。
事实上,大部分编译器都是使用栈来实现递归的。
当调用一个方法时,编译器会把这个方法的所有参数及其返回地址都压入栈中,然后把控制权交给这个方法。当这个方法返回时,这些值退栈,参数消失了,并且控制权重新回到返回地址处。
A: 任意一个递归方法都可以转换为基于栈的方法来模拟,一个方法的内部实现大致经历如下几步:
- 当一个方法被调用时,它的形参以及返回地址被压入一个栈中;
- 这个方法可以通过获取栈顶元素的值来访问它的参数;
- 当这个方法要返回时,它查看栈以获得返回地址,然后这个地址以及方法的所有形参退栈,并且销毁。
Q: 如何用栈模拟一个递归?
A: 我们以三角数字的递归转化为基于栈的方法来说明,示例:TriangleNumber.java,如下图:
函数的执行可根据6个指令地址来执行每一个细微的逻辑:
1) 初次调用会执行0x01地址的指令,把用户输入的值以及函数返回值地址0x06压入栈;
2) 在函数的入口0x02,会检查它的参数是否为1(通过栈顶元素获取),如果参数是1,这就是基值条件,则将控制权交给0x05(即函数出口)执行。
如果参数不是1,则将递归地调用自身(0x03),这个递归的调用由参数n-1和返回值地址0x04入栈,以及控制权交给0x02执行。
3) 从递归调用返回的过程中,0x04执行了函数返回值加上它的参数n,然后这个方法退出0x05。
4) 当函数退出时,最后的Param对象退栈,这个信息不再需要。因此会执行0x06结束while死循环。 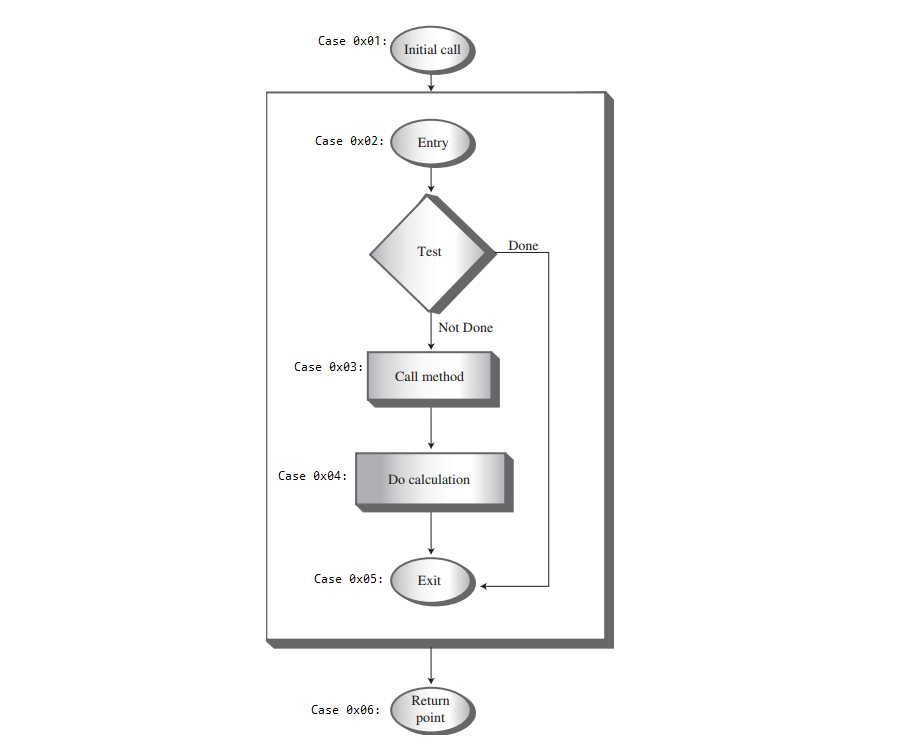
一些有趣的递归应用
Q: 求一个数的乘方?
A: 比如2^8,我们可以会求表达式2*2*2*2*2*2*2*2的值,但是如果y的值很大,这个会显得表达式很冗长。那么由没有更快一点方法呢?一个解决的方法是重新组织这个问题,只要可能就拿2的方次相乘,而不是乘以2。
A: 这个方案以数学等式xy=(x2)y/2为基础。可以使用递归的思路来解决这个问题,基值条件就是当y=1的时候就返回。
A: 如下图,是以318为例的递归过程,其中要注意递归在返回的过程中,只要y是一个奇数,就得额外地乘以一个x。 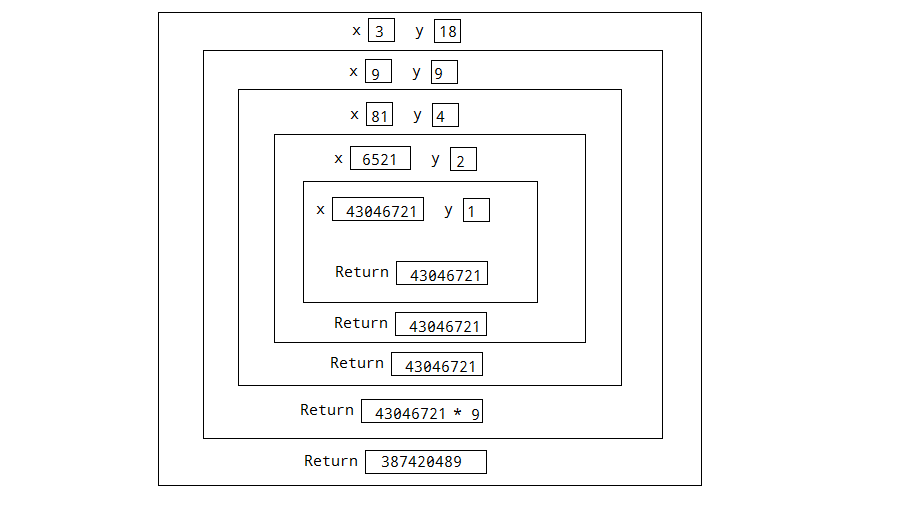
A: 示例:Math.java
Q: 背包问题(The Knapsack Problem)?
A: 背包问题是计算机科学中的经典问题,在最简单的形式中,包括试图将不同重量的数据项放到背包中,以使背包最后达到了指定的总重量。不需要把所有的选项都放入背包中。
A: 假设想要让背包精确地承重20磅,并且有 5 个可以放入的数据项,它们的重量分别是11 磅,8 磅,7 磅,6 磅,5 磅。这个问题可能对于人类来说很简单,我们大概就可以计算出8磅+7磅 + 5磅=20磅。但是如果让计算机来解决这个问题,就需要给计算机设定详细的指令了。
算法如下:
1) 如果在这个过程的任何时刻,选择的数据项的总和符合目标重量,那么工作便完成了。
2) 从选择的第一个数据项开始,剩余的数据项的加和必须符合背包的目标重量减去第一个数据项的重量,这是一个新的目标重量。
3) 逐个的试每种剩余数据项组合的可能性,但是注意不要去试所有的组合,因为只要数据项的和大于目标重量的时候,就停止添加数据。
4) 如果没有合适的组合,放弃第一个数据项,并且从第二个数据项开始再重复一遍整个过程。
5) 继续从第三个数据项开始,如此下去直到你已经试验了所有的组合,这时才知道有没有解决方案。
A: 示例:Knapsack.java
Q: 组合:选择一支队伍?
A: 在数学中,组合是对事物的一种选择,而不考虑他们的顺序。
A: 比如有5个登山队员,名称为 A,B,C,D和E。想要从这五个队员中选择三个队员去登峰,这时候如何列出所有的队员组合。(不考虑顺序)
如何来写这样一个程序打印所有的组合呢?ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE
A: 使用递归的解决方案,它包括把这些组合分成两个部分:由A开始的组合和不是由A开始的组合。假设把从5个人中选出3个人的组合简写为(5,3)。规定n是这群人的大小,并且K是组队的大小。那么根据法则可以得到:
(n, k)=(n-1, k-1)+(n-1, k)
A: 可以把这个问题看成是一棵树,在第一行是(5,3),在第二行是(4,3)和(4,2),依次类推,这个树中的节点对应于递归方法的调用,下图显示了例子(5,3)的样子。 
基值条件是指没有意义的组合:某个数字是0以及队员数大于人群数的情况。组合(1,1)是合法的,但是继续分解它就没有必要了。在这个图中,虚线表示了基值条件,这时需要返回,而不是继续分解了。
A: 当沿着树往下走时,需要记住访问过的节点序列。这如何做到呢? 示例:Combination.java
小结
- 一个递归的方法每次用不同的参数值反复调用自身
- 某种参数值使递归的方法返回,而不再调用自身,这种称为基值条件
- 当递归方法返回时,递归过程通过逐渐完成各层方法实例的未执行部分,而从最内层返回到最外层的原始调用处
- 一个单词的全排列可以通过反复地轮换它的字母以及全排列它最右边的n-1个字母来递归得到
- 任何可以用递归完成的操作都可以用一个栈来实现
- 递归的方法可能效率低,如果是这样的话,有时可以用一个简单的循环或者一个基于栈的方法来替代它
参考
- 《Java数据结构和算法》Robert Lafore 著,第6章 - 递归
