0902测试（垫底）

自开学以后，效率奇低。

洛谷P3938 斐波那契

题目描述

  小 C 养了一些很可爱的兔子。 有一天，小 C 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍：一对兔子从出生后第二个月起，每个月刚开始的时候都会产下一对小兔子。我们假定， 在整个过程中兔子不会出现任何意外。

  小 C 把兔子按出生顺序，把兔子们从 1 开始标号，并且小 C 的兔子都是 1 号兔子和 1 号兔子的后代。如果某两对兔子是同时出生的，那么小 C 会将父母标号更小的一对优先标 号。

  如果我们把这种关系用图画下来，前六个月大概就是这样的：

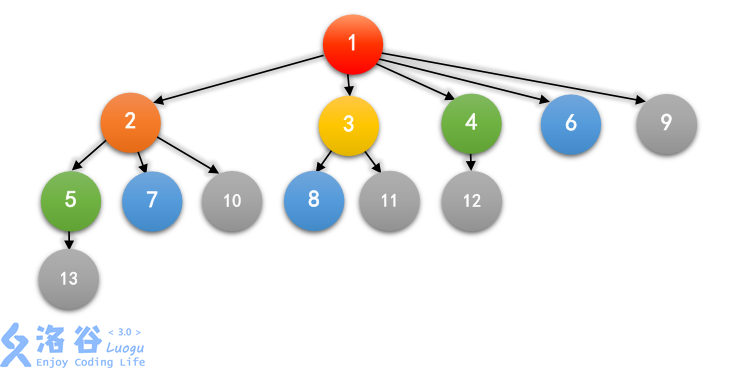
  其中，一个箭头 A → B 表示 A 是 B 的祖先，相同的颜色表示同一个月出生的兔子。
  为了更细致地了解兔子们是如何繁衍的，小 C 找来了一些兔子，并且向你提出了 m 个 问题：她想知道关于每两对兔子 a_i 和 b_i​ ，他们的最近公共祖先是谁。你能帮帮小 C 吗？
  一对兔子的祖先是这对兔子以及他们父母（如果有的话）的祖先，而最近公共祖先是指 两对兔子所共有的祖先中，离他们的距离之和最近的一对兔子。比如，5 和 7 的最近公共祖 先是 2，1 和 2 的最近公共祖先是 1，6 和 6 的最近公共祖先是 6。
输入格式
  从标准输入读入数据。 输入第一行，包含一个正整数 m。 输入接下来 m 行，每行包含 2 个正整数，表示 aia_iai​ 和 bib_ibi​ 。
输出格式
  输出到标准输出中。 输入一共 m 行，每行一个正整数，依次表示你对问题的答案。
输入输出样例

  输入 #1
  5
  1 1
  2 3
  5 7
  7 13
  4 12
  输出 #1
  1
  1
  2
  2
  4

解析

  第一眼看到这题是懵逼的，因为我连斐波那契数列的递推式都不知道为什么是那个亚子

  手玩一会后发现还是可做的

  斐波那契数列的递推式f[i]=f[i-1]+f[i-2]

  f[i-1]表示i-1月时有多少只兔子，它应该加上新生的兔子数量，而新生的兔子数量与能繁殖的兔子的数量相等

  而在i-1月时能繁殖的兔子的数量就是f[i-2]

  所以新的兔子都是前f[i-2]只兔子生的。

  所以f[i-1]+1,f[i-1]+2,f[i-1]+3......f[i]-1,f[i]的父亲分别是1,2,3......f[i-2],即1,2,3......f[i]-f[i-1]

  所以，对于每个兔子，拿它的编号减去最大的小于它的斐波那契数就可以得到它的父亲。

  然后暴力求公共祖先就行了。

  另外，对于所有的兔子，每个斐波那契数最多减去一次，因为f[i]<f[i-1]*2  ,  f[i]-f[i-1]<f[i-1]

  代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,en1,en2;
long long a,b,q1[65],q2[65],fib[65];
int main()
{
    fib[1]=1ll;fib[2]=2ll;
    for(int i=3;i<=62;i++)fib[i]=fib[i-1]+fib[i-2];
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld",&a,&b);
        q1[en1=1]=a;q2[en2=1]=b;
        for(int k=60;k;k--)
        {
            if(q1[en1]>fib[k])en1++,q1[en1]=q1[en1-1]-fib[k];
            if(q2[en2]>fib[k])en2++,q2[en2]=q2[en2-1]-fib[k];
        }
        while(en1>1&&en2>1&&q1[en1-1]==q2[en2-1])en1--,en2--;
        printf("%lld
",q1[en1]);
    }
}

洛谷P3939 数颜色

题目描述

 小 C 的兔子不是雪白的，而是五彩缤纷的。每只兔子都有一种颜色，不同的兔子可能有 相同的颜色。小 C 把她标号从 1 到 n 的 n 只兔子排成长长的一

排，来给他们喂胡萝卜吃。 排列完成后，第 i 只兔子的颜色是 ai​。俗话说得好，“萝卜青菜，各有所爱”。

小 C 发现，不同颜色的兔子可能有对胡萝卜的

不同偏好。比如，银色的兔子最喜欢吃金色的胡萝卜，金色的兔子更喜欢吃胡萝卜叶子，而 绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要

求，小 C 十分苦恼。所以，为了使得胡萝卜喂得更加准确，小 C 想知道在区间 [l_j,r_j] 里有多少只颜色为 c_j的兔子。

不过，因为小 C 的兔子们都十分地活跃，它们不是很愿意待在一个固定的位置；与此同时，小 C 也在根据她知道的信息来给兔子们调整位置。所以，

有时编号为 x_j和 x_j+1的两 只兔子会交换位置。 小 C 被这一系列麻烦事给难住了。你能帮帮她吗？

输入格式

从标准输入中读入数据。 输入第 1 行两个正整数 n,m。

输入第 2 行 n个正整数，第 i 个数表示第 i只兔子的颜色 a_i​。

输入接下来 mmm 行，每行为以下两种中的一种：

“1 l_j r_j c_j​” ：询问在区间 [l_j,r_j] 里有多少只颜色为 c_j​的兔子；

“2 x_j​”：x_j​ 和 x_j+1两只兔子交换了位置。

输出格式

输出到标准输出中。

对于每个 1 操作，输出一行一个正整数，表示你对于这个询问的答案。

输入 #1
6 5
1 2 3 2 3 3 
1 1 3 2
1 4 6 3 
2 3
1 1 3 2 
1 4 6 3
输出 #1
1
2
2
3

解析

  一开始还以为是什么毒瘤数据结构，但一看交换只是相邻的交换

  我们考虑每种颜色看一个vector,一开始把相同颜色的坐标从小到大放进去

  显然每个vector都是单增的

  我们试着维护它的单调性

  如果交换的两个颜色异色，那么就二分它们在vector中的位置，找到后坐标加1

  因为两个颜色相邻，所以并不影响数组的单调性

  而如果两个颜色相同，我们就没有必要去换。

  查询的话，直接二分就好了，注意特判一下不存在的情况（不然就像我一样丢80分）

  （考试下来才知道lower_bound套vector的话要写begin和end）

  代码

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
vector<int>g[300005];
int n,m,co[300005];
int check(int x,int c)
{
    int l=0,r=g[c].size()-1,ans=0,mid;
    while(l<=r)
    {
        mid=(l+r)/2;
        if(x<=g[c][mid])ans=mid,r=mid-1;
        else l=mid+1;
    }
    return ans;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&co[i]),g[co[i]].push_back(i);
    for(int i=1,op,l,r,c,x;i<=m;i++)
    {
        scanf("%d",&op);
        if(op==1)
        {
            scanf("%d%d%d",&l,&r,&c);
            if(g[c].size()==0){puts("0");continue;}
            if(g[c][g[c].size()-1]<l){puts("0");continue;}
            if(g[c][g[c].size()-1]<r){printf("%d
",g[c].size()-check(l,c));continue;}
            int l1=check(l,c),r1=check(r,c);printf("%d
",r1-l1+(g[c][r1]==r));
        }
        if(op==2)
        {
            scanf("%d",&x);
            if(co[x]==co[x+1])continue;
            int x1=check(x,co[x]),x2=check(x+1,co[x+1]);
            g[co[x]][x1]++;g[co[x+1]][x2]--;swap(co[x],co[x+1]);
        }
    }
}

洛谷P3940 分组

题目描述

  小 C 在了解了她所需要的信息之后，让兔子们调整到了恰当的位置。小 C 准备给兔子 们分成若干个小组来喂恰当的胡萝卜给兔子们吃。

  此时， n 只兔子按一定顺序排成一排，第 i 只兔子的颜色是 a_​i 。由于顺序已经是被 调整好了的，所以每个小组都应当是序列上连续的一段。

  在分组前，小 C 发现了一个规律：有些兔子会两两发生矛盾。并且，两只兔子会发生矛 盾，当且仅当代表他们的颜色的数值之和为一个正整数的平方。

  比如，1色兔子和2色兔子 不会发生矛盾，因为3不是任何一个正整数的平方；而 1 色兔子却会和 3 色兔子发生矛盾， 因为 4=2^2。小 C 认为，

  只要一个小组内的矛盾不要过大就行。因此，小 C 定义了一个小组的矛盾值 k，表示在这个小组里，至少需要将这个组再一次分成 k 个小团体；

  每个小团体并不需 要是序列上连续的一段，但是需要使得每个小团体内任意两只兔子之间都不会发生矛盾。

  小C要求，矛盾值最大的小组的矛盾值 k 不超过 K 就可以了。当然，这样的分组方法可能会有很多个；为了使得分组变得更加和谐，小 C 想知道，

  在保证分组数量最少的情况下，字典序最小的方案是什么。你能帮帮她吗？

  字典序最小的方案是指，按顺序排列分组的间隔位置，即所有存在兔子 i 和 i+1 在 不同组的位置 i，

  和其它所有相同分组组数相同的可行方案相比总有第一个不同的位置比其 它方案小的方案。

输入格式

  从标准输入中读入数据。输入第 1 行两个正整数 n,K。

  输入第 2 行 n 个正整数，第 i 个数表示第 i 只兔子的颜色 a_i​。

输出格式

  输出到标准输出中。输出第 1 行一个正整数 m，为你至少需要将兔子分为多少个小组。输出第 2 行m−1个从小到大的排列的正整数，第 i 个数 s_i表示

  s_i和s_i+1在你的方案里被分到了两个小组。如果 m=1，那么请输出一个空行。

输入输出样例

  输入
  5 2
  1 3 15 10 6
  输出
  2
  1

解析

  先考虑字典序最小如何解决。

  考虑已经将前面i个分好组，如果第i+1个能和第i个分为一组，为了组数最小就应该加入前面的组，因为i+1如果分到前面，它对后面的组不会产生限制。

  所以能加入前面组时尽量加。但这样只能让组数最小，而且会让相同组数时字典序最大。不过我们可以倒过来处理，最后再倒回来就好了。

  观察数据发现就两种情况，K=1和K=2。

  当K=1的时候，直接倒过来贪心处理，能和之前的兔子分为一组就分成一组，用一个数组映射一下每种颜色的兔子有多少只，加入时直接查询是否有与它矛盾的颜色，如果有就新开一组。

  当K=2的时候，如果把两种颜色之间有矛盾看作点与点之间有边，那么在一个组里的颜色代表的点连边后必须构成一个二分图。

  那么我们用带权并查集维护，当加入一个兔子时，看它颜色所代表的点与当前图中哪些点能连边。连边时，如果发现两个点属于同一个连通块且到根节点的距离的奇偶性相等，那么新加入的边就会让它们形成奇环，无法构成二分图，那么就应该直接新开一组。

  另外，注意自环（即一种颜色与自己矛盾）。若一种与自己矛盾的颜色的个数超过1，那么就不能再有其他颜色与它们矛盾，否则必定构成奇环。

  代码如下

#include<map>
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=131075;vector<int>G[maxn];
int n,K,cnt,a[maxn],mp[maxn*2+5],ans[maxn],ori[maxn*2+5],val[maxn*2+5],isa[maxn*2+5];
int find(int x){if(!ori[x])return x;int t=ori[x];ori[x]=find(ori[x]);val[x]^=val[t];return ori[x];}
void solve1()
{
    mp[a[1]]=1;
    for(int i=2;i<=n;i++)
    {
        int flag=0;for(int j=512;j>=0&&j*j>=a[i];j--)flag|=mp[j*j-a[i]];
        if(flag){ans[++cnt]=i;for(int j=ans[cnt-1];j<=ans[cnt];j++)mp[a[j]]=0;}mp[a[i]]=1;
    }
    printf("%d
",cnt+1);for(int i=cnt;i;i--)printf("%d%c",n-ans[i]+1,i==1?'
':' ');if(!cnt)puts("");
}
void solve2()
{
    for(int i=1;i<=131072;i++)for(int j=1;j*j<=i+131072;j++)if(j*j>i)G[i].push_back(j*j-i);
    for(int i=0;i*i<=131072*2;i+=2)isa[i*i/2]=1;mp[a[1]]=1;
    for(int i=2,flag=0;i<=n;mp[a[i]]++,flag=0,i++)
    {
        if(mp[a[i]]>=2&&isa[a[i]])flag=1;
        else
        {
            if(mp[a[i]]&&isa[a[i]])
                for(int j=0,lim=G[a[i]].size();j<lim&&!flag;j++)
                    flag|=(mp[G[a[i]][j]]&&G[a[i]][j]!=a[i]);
            else
                for(int j=0,lim=G[a[i]].size();j<lim&&!flag;j++)
                {
                    int fx=find(a[i]),fy=find(G[a[i]][j]);if(!mp[G[a[i]][j]])continue;
                    if(isa[G[a[i]][j]]&&mp[G[a[i]][j]]>=2)flag=1;
                    if(fx!=fy){ori[fx]=fy;val[fx]=val[G[a[i]][j]]^val[a[i]]^1;}
                    if(fx==fy&&val[a[i]]==val[G[a[i]][j]])flag=1;
                }
        }
        if(flag){ans[++cnt]=i;for(int j=ans[cnt-1];j<=ans[cnt];j++)mp[a[j]]=0,ori[a[j]]=0,val[a[j]]=0;}
    }
    printf("%d
",cnt+1);for(int i=cnt;i;i--)printf("%d%c",n-ans[i]+1,i==1?'
':' ');if(!cnt)puts("");
}
int main()
{
    scanf("%d%d",&n,&K);
    for(int i=n;i;i--)scanf("%d",&a[i]);
    if(K==1){solve1();return 0;}
    if(K==2){solve2();return 0;}
}