题目:给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素
归并排序
思路及算法
由题目给出的性质可知,这个矩阵的每一行均为一个有序数组。问题即转化为从这 n 个有序数组中找第 k 大的数,可以想到利用归并排序的做法,归并到第 k 个数即可停止。
一般归并排序是两个数组归并,而本题是 n 个数组归并,所以需要用小根堆维护,以优化时间复杂度。
public int kthSmallest2(int[][] matrix, int k){
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
@Override
public int compare(int[] a, int[] b) {
return a[0] - b[0];
}
});
int n = matrix.length;
for (int i = 0; i < n; i++) {
pq.offer(new int[]{matrix[i][0], i, 0});
}
//维护最左侧的一列最小值候选人,当有序队列弹出7个最小值,此时队列中的最小值即为所求
for (int i = 0; i < k - 1; i++) {
int[] now = pq.poll();
if (now[2] != n - 1) {
pq.offer(new int[]{matrix[now[1]][now[2] + 1], now[1], now[2] + 1});
}
}
return pq.poll()[0];
}
时间复杂度:O(klogn),归并 k 次,每次堆中插入和弹出的操作时间复杂度均为logn。
空间复杂度:O(n),堆的大小始终为 n。
其实解决这个问题的关键,在于维护一组“最小值候选人”
在整个矩阵中,每次弹出矩阵中最小的值,第k个被弹出的就是我们需要的数字。
现在我们的目的很明确:每次弹出矩阵中最小的值。你需要保证最小值必然从这组候选人中产生,于是每次只要从候选人中弹出最小的一个即可。
我们来选择第一组候选人,在这里可以选择第一列,因为每一个数字都是其对应行的最小值,全局最小值也必然在其中。然后使用ProrityQueue有序队列来存储这一组候选人,就能保证每次从队列中弹出的都是候选人中的最小值。
例:
选取以下矩阵,开始的候选人为第一列,然后每次选择候选人中的最小值弹出,然后被弹出的那一行的候选人右移以为记得到该行新的候选人,当某一行的值弹完后将候选人队列中长度减1即可,知道弹出第k-1个值,此时最小值队列的值即为所求第k小的值。
步骤如下图所示:
二分查找
思路及算法
由题目给出的性质可知,这个矩阵内的元素是从左上到右下递增的(假设矩阵左上角为 matrix[0][0])。以下图为例:
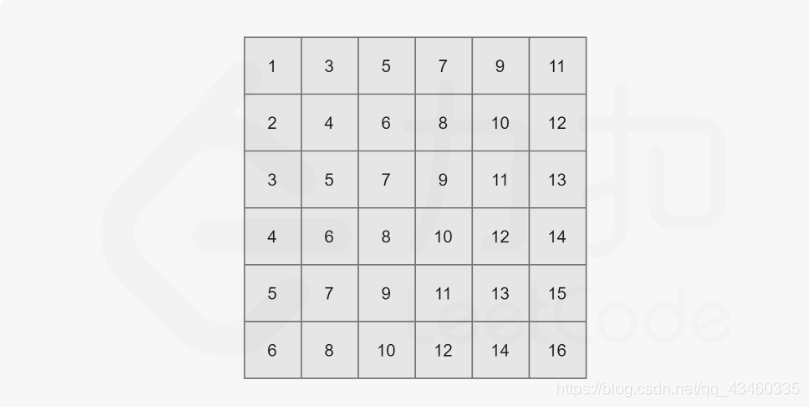
我们知道整个二维数组中 matrix[0][0] 为最小值,matrix[n−1][n−1] 为最大值,现在我们将其分别记作 l 和 r。
可以发现一个性质:任取一个数 mid 满足l≤mid≤r,那么矩阵中不大于 mid 的数,肯定全部分布在矩阵的左上角。
例如下图,取 mid=8:
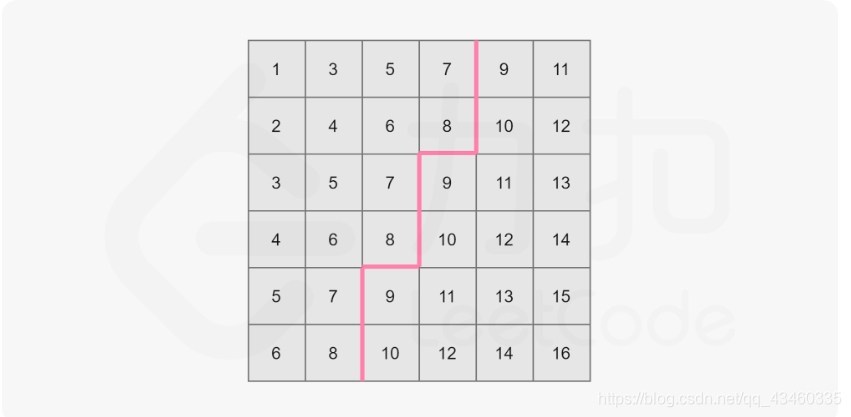
我们可以看到,矩阵中大于 mid 的数就和不大于 mid 的数分别形成了两个板块,沿着一条锯齿线将这个矩形分开。其中左上角板块的大小即为矩阵中不大于 mid 的数的数量。
我们只要沿着这条锯齿线走一遍即可计算出这两个板块的大小,也自然就统计出了这个矩阵中不大于mid 的数的个数了。
走法演示如下,依然取 mid=8:
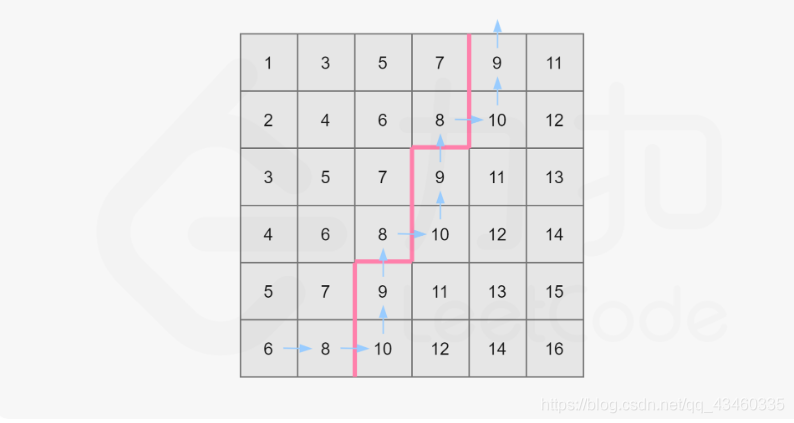
可以这样描述走法:
1、初始位置在 matrix[n−1][0](即左下角);
2、设当前位置为 matrix[i][j]。若 matrix[i][j]≤mid,则将当前所在列的不大于 mid 的数的数量(即 i+1)累加到答案中,并向右移动,否则向上移动;
3、不断移动直到走出格子为止。
我们发现这样的走法时间复杂度为 O(n),即我们可以线性计算对于任意一个 mid,矩阵中有多少数不大于它。这满足了二分查找的性质。
不妨假设答案为 x,那么可以知道 l≤x≤r,这样就确定了二分查找的上下界。
每次对于「猜测」的答案 mid,计算矩阵中有多少数不大于mid :
如果数量不少于 k,那么说明最终答案 x 不大于 mid;
如果数量少于 k,那么说明最终答案 x 大于 mid。
这样我们就可以计算出最终的结果 x 了。
public int kthSmallest3(int[][] matrix, int k){
int n = matrix.length;
int left = matrix[0][0];
int right = matrix[n - 1][n - 1];
while (left < right) {
int mid = left + ((right - left) >> 1);
if (check(matrix, mid, k, n)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
//判断数量是否大于k
public boolean check(int[][] matrix, int mid, int k, int n) {
int i = n - 1;
int j = 0;
int num = 0;
while (i >= 0 && j < n) {
if (matrix[i][j] <= mid) {
num += i + 1;
j++;
} else {
i--;
}
}
return num >= k;
}
时间复杂度:O(nlog(r−l)),二分查找进行次数为 O(log(r−l)),每次操作时间复杂度为 O(n)。
空间复杂度:O(1)。
暴力法:直接排序
public int kthSmallest(int[][] matrix, int k) {
int rows = matrix.length;
int columns = matrix[0].length;
int []sorted = new int[rows*columns];
int index = 0;
for (int[] row : matrix) {
for (int num : row) {
sorted[index++] = num;
}
}
Arrays.sort(sorted);
return sorted[k-1];
}
时间复杂度:O(n^2logn),对 n^2个数排序。
空间复杂度:O(n^2),一维数组需要存储这 n^2个数。
暴力法容易理解,就是直接先把二维数组转换为一维数组,然后对该一维数组排序(调用Arrays.sort()函数即可),然后排序后数组中下标为k-1的值即为所求,但是这种方法没有用到有序数组的性质,而且新产生了一个n*n的一维数组,所以时间和空间复杂度都很高。
其它方法自行查看Leetcode官方题解。
参考:
Leetcode题解1
Leecode官方题解