隐马尔科夫

一、马尔科夫链

1.马尔科夫链：指数学中具有马尔可夫性质的离散时间随机过程。即给定当前知识或信息的情况下，过去对于未来预测无关，的这样一种前后关系。

2.马尔科夫性质：初始状态确定的情况下，给定不变的状态转移矩阵，n次循环之后最终会达到稳态的分布。下面例子中，达到稳态后，在很久的未来，每一天的天气都是q=(0.833 0.167)的一个样本点。下面一阶马尔科夫过程定义了三个部分：（1）状态：晴天、阴天。（2）初始向量 ：定义系统在时间0的时候的状态的概率。比如晴天，阴天是（1,0）（3）状态转移矩阵：每种天气转换的概率。

3.马尔科夫链的缺陷很明显，前后关系的缺失，带来了信息的缺失。比如股市，如果观测市场，我们只能知道当天的成交价格、成交量等信息，我们并不知道当前股市处于什么样的状态（牛市、熊市、震荡、反弹等等）。在这种情况下，我们有两个状态集合，一个是可以观察的状态集合（股市价格成交量状态等）和一个隐藏的状态集合（股市状况）。这时候需要多一层马科夫链，隐马尔可夫HMM。

二、隐马尔科夫链

1．HMM是关于时序的概率模型，描述由一个隐藏的马尔科夫链生成不可观察的状态随机序列（z），再由各个状态生成观测随机序列(x)的过程。与LDA模型的假设不同(文档中的词都是独立的)，HMM中x1, x2…之间是不独立的（在z1，z2…不可知的情况下）。

2.HMM的参数描述

首先我们来看如何描述Zn-1到Zn的状态，假设Zn-1由n个取值，Z n也有n个取值，当Zn-1取值为i时，Z n等于j的概率（状态转移的条件概率矩阵An*n）。

Zn到Xn的状态，当Zn取值为i时，Xn等于j的概率（观测概率分布Bn*m）。如果m=n且为单位阵时，则HMM模型就退化为了MM模型（z1, z2…zn），相当于B的存在把我们这些未观测的值z1 z2…做了混淆，所以有些教程将B称为混淆矩阵。另外，观察变量X也可能是连续的变量服从N（x| μ，xigema）。

其次，我们还差一个初始Z1的分布，取第一个不可观察状态Z1的概率为π1，取第二个不可观察状态Z2的概率为π2…

因此把上面三个罗列后我们可知，对于隐马尔可夫模型想去确定参数，就是来计算初始概率分布π、状态转移概率分布A（一定是方正）以及观测概率分布B（不一定是方正），简写记做lamda。

λ=（A,B,π）

3.隐马尔科夫链的三大问题：
evaluation:知道隐含状态的数量、转换概率和可见状态链，求掷出这个结果的概率。

Recognition:知道隐含状态的数量、转换概率和可见状态链，求隐含状态链，比如你说出来的是东北话，我们想知道的是你表达的含义是什么。
Training:知道隐含状态的数量和可见状态链，反推出每个隐含状态是什么和转换概率，模型lambda本身不确定，需要观测序列就是这样，则需要隐马尔可夫的模型是什么样子。

解决方法：

最后可观测状态是Walk Shop Clean
问题一，forward algorithm，向前算法，或者Backward Algo向后算法。时间序列的形式，以第一个时间为基础往后推。（动态规划）

问题二，Viterbi Algo，维特比算法。暴力排列所有的情况，那个排列使得到达终结点情况的概率最大。（动态规划）空间换时间，把每次能达到最大概率的中间点记录下来。

问题三，Baum-Welch Algo, 鲍姆-韦尔奇算法。只能得到局部最优解。（EM算法）。

ε_ij的意思是，从t到t+1，状态从i到j发生的最大概率。

三、 应用马尔科夫链做词性标准
HMM可用标注问题，在语音识别、NLP、生物信息、模式识别等领域，被实践证明是有效的算法。应用比较多的就是用于中文分词，同时它还具有发现新词的功能。在没有给定词库的情况下HMM也可以进行分词（参数斯塔），（https://www.jianshu.com/p/f140c3a44ab6 ）只是会把很多词都作为新词处理。Jieba分词默认的分词模型就是HMM模型
NLTK有自带的hmm，YAHMM等库可以直接应用。但下面主要是应用viterber自己写出词性标准的算法。
根据语法的规则，我们会知道各词性之间的转移。基于这个语法Model，就可以画出双层的隐马尔科夫结构。

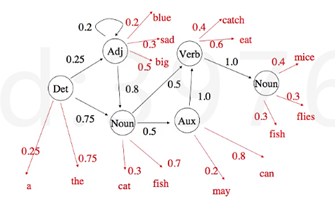
通过语料库corpus，总结出模型后（λ=（π，A, B）），再给新的句子做词性标注。求在单词w1…w2确定的情况下，出这个t1…tn词性标注的概率。

链式法则求解，后面取决于前面状态的条件概率形式。

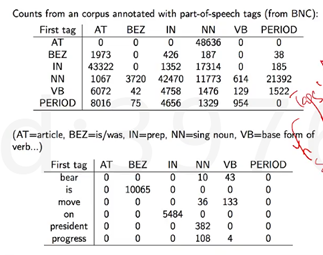
怎么计算出上面表达式呢，Aij的计算是把所有i在前j在后的tag的次数/所有出现i的tag的次数。B是在这个tag下能出单词w的概率，其计算方法是tag是k的情况下出的单词是w的次数/tag等于k的次数。在所有句子的开头加一个start，πinit就等于从start到所有tags的概率分布。

给出一句话，找出最符合的tags，HMM的问题二，要用到vertibi算法。找出最优的tags路径，使得下面这四个单词出现的概率最大。

#代码 NLTK有自带的hmm，YAHMM等库可以直接应用。但下面主要是应用viterber自己写出词性标准的算法。

import nltk
import sys
from nltk.corpus import brown
# 给词们加上开始和结束的符号
brown_tags_words = [ ]
for sent in brown.tagged_sents():
    # 先加开头
    brown_tags_words.append( ("START", "START") )
    # 为了省事儿，我们把tag都省略成前两个字母
    brown_tags_words.extend([ (tag[:2], word) for (word, tag) in sent ])
    # 加个结尾
    brown_tags_words.append( ("END", "END") )
#词统计
#B 计算P(wi | ti) = count(wi, ti) / count(ti)
# conditional frequency distribution
cfd_tagwords = nltk.ConditionalFreqDist(brown_tags_words)
# conditional probability distribution
cpd_tagwords = nltk.ConditionalProbDist(cfd_tagwords, nltk.MLEProbDist)
#看下统计结果
print("The probability of an adjective (JJ) being 'new' is", cpd_tagwords["JJ"].prob("new"))

#A 计算P(ti | t{i-1}) = count(t{i-1}, ti) / count(t{i-1})
brown_tags = [tag for (tag, word) in brown_tags_words ]
# count(t{i-1} ti)
# bigram的意思是 前后两个一组，联在一起
cfd_tags= nltk.ConditionalFreqDist(nltk.bigrams(brown_tags))
# P(ti | t{i-1})
cpd_tags = nltk.ConditionalProbDist(cfd_tags, nltk.MLEProbDist)
#查看效果
print("If we have just seen 'DT', the probability of 'NN' is", cpd_tags["DT"].prob("NN"))
#那么，比如， 一句话，"I want to race"， 一套tag，"PP VB TO VB"
#他们之间的匹配度有多高呢？
#其实就是：P(START) * P(PP|START) * P(I | PP) *P(VB | PP) * P(want | VB) *P(TO | VB) * P(to | TO) *P(VB | TO) * P(race | VB) *P(END | VB)
prob_tagsequence = cpd_tags["START"].prob("PP") * cpd_tagwords["PP"].prob("I") * 
    cpd_tags["PP"].prob("VB") * cpd_tagwords["VB"].prob("want") * 
    cpd_tags["VB"].prob("TO") * cpd_tagwords["TO"].prob("to") * 
    cpd_tags["TO"].prob("VB") * cpd_tagwords["VB"].prob("race") * 
    cpd_tags["VB"].prob("END")

print( "The probability of the tag sequence 'START PP VB TO VB END' for 'I want to race' is:", prob_tagsequence)

#viterbi实现，如果我们手上有一句话，怎么知道最符合的tag是哪一组。
#首先，我们拿出所有独特的tags（也就是tags的全集）
distinct_tags = set(brown_tags)
# 初始π计算 把跟start相连的第一组都计算出来
viterbi = [ ]
backpointer = [ ]
first_viterbi = { }
first_backpointer = { }
for tag in distinct_tags:
    # don't record anything for the START tag
    if tag == "START": continue
    first_viterbi[ tag ] = cpd_tags["START"].prob(tag) * cpd_tagwords[tag].prob( sentence[0] )
    first_backpointer[ tag ] = "START"
print(first_viterbi)
print(first_backpointer)
#接下来，把楼上这些，存到Vitterbi和Backpointer两个变量里去
viterbi.append(first_viterbi)
backpointer.append(first_backpointer)

# 开始Loop
for wordindex in range(1, len(sentence)):
    this_viterbi = { }
    this_backpointer = { }
    prev_viterbi = viterbi[-1]
    for tag in distinct_tags:
        # START没有卵用的，我们要忽略
        if tag == "START": continue
# 如果现在这个tag是X，现在的单词是w，
        # 我们想找前一个tag Y，并且让最好的tag sequence以Y X结尾。
        # 也就是说
        # Y要能最大化：
        # prev_viterbi[ Y ] * P(X | Y) * P( w | X)
        best_previous = max(prev_viterbi.keys(),key = lambda prevtag: prev_viterbi[ prevtag ] * cpd_tags[prevtag].prob(tag) * cpd_tagwords[tag].prob(sentence[wordindex]))
        this_viterbi[ tag ] = prev_viterbi[ best_previous] * cpd_tags[ best_previous ].prob(tag) * cpd_tagwords[ tag].prob(sentence[wordindex])
        this_backpointer[ tag ] = best_previous
    # 每次找完Y 我们把目前最好的 存一下
    currbest = max(this_viterbi.keys(), key = lambda tag: this_viterbi[ tag ])
print( "Word", "'" + sentence[ wordindex] + "'", "current best two-tag sequence:", this_backpointer[ currbest], currbest)
# 完结
# 全部存下来
viterbi.append(this_viterbi)
backpointer.append(this_backpointer)

#找end结束
# 找所有以END结尾的tag sequence
prev_viterbi = viterbi[-1]
best_previous = max(prev_viterbi.keys(), key = lambda prevtag: prev_viterbi[ prevtag ] * cpd_tags[prevtag].prob("END"))
prob_tagsequence = prev_viterbi[ best_previous ] * cpd_tags[ best_previous].prob("END")
# 我们这会儿是倒着存的。。。。因为。。好的在后面
best_tagsequence = [ "END", best_previous ]
# 同理 这里也有倒过来
backpointer.reverse()

#最终：回溯所有的回溯点，此时，最好的tag就是backpointer里面的current best
current_best_tag = best_previous
for bp in backpointer:
    best_tagsequence.append(bp[current_best_tag])
current_best_tag = bp[current_best_tag]
#显示结果
best_tagsequence.reverse()
print( "The sentence was:", end = " ")
for w in sentence: print( w, end = " ")
print("
")
print( "The best tag sequence is:", end = " ")
for t in best_tagsequence: print (t, end = " ")
print("
")
print( "The probability of the best tag sequence is:", prob_tagsequence)