AdaboostGBDTGBRT组合算法(龙心尘老师上课笔记)
一、Bagging (并行bootstrap)& Boosting(串行)
随机森林实际上是bagging的思路,而GBDT和Adaboost实际上是boosting的思路。而bagging和boosting有什么区别呢?怎样从bagging转到boosting呢?
Bagging的假设函数:
如果是二分类问题: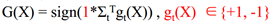 ,其中T是分类器的总数,g(x)是其中的小分类器的取值(+1或-1),最后根据各个分类器的值求加和,根据和的符号得到最终大分类器是正还是负。
,其中T是分类器的总数,g(x)是其中的小分类器的取值(+1或-1),最后根据各个分类器的值求加和,根据和的符号得到最终大分类器是正还是负。
如果是回归问题: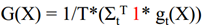 ,最后取得是各个小分类器的平均值。
,最后取得是各个小分类器的平均值。
Bagging的特点1.各个学习器相互独立,可以同时并行生成;2.各个学习期权重相同
而Boosting特别大的区别就在于,各个学习器强烈依赖(上一个学习器产生,再产生下一个),串行生成,其中,gbdt(每个学习器权重相同),Adaboost(每个学习器权重不同)。
Boosting要解决的核心问题:
产生不同的训练集(训练集各样本标签不同,训练集各样本抽样权重不同)
产生不同的模型(不同的训练集,就能产生不同模型)
产生不同模型对应的权重
二、GBDT(生成新标签,串行生成树)
假设函数: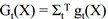
损失函数:均方损失函数
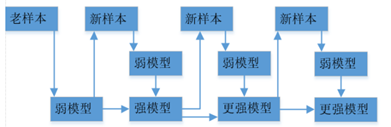
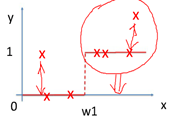
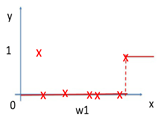
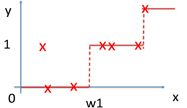
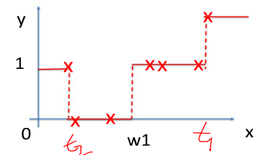
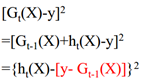 其中红色部分是之前集成学习器产生的残差,对应来看,这样可以理解成,红色部分相当于可以把之前学习器的残差,作为原来样本的新标签。这样就产生了新的训练集可以生成新的模型(下面右图2)。集成弱模型,得到强模型(下图3,样本x不变,标签Y变),依次下去重复,直到集合成最强模型。
其中红色部分是之前集成学习器产生的残差,对应来看,这样可以理解成,红色部分相当于可以把之前学习器的残差,作为原来样本的新标签。这样就产生了新的训练集可以生成新的模型(下面右图2)。集成弱模型,得到强模型(下图3,样本x不变,标签Y变),依次下去重复,直到集合成最强模型。
损失函数:
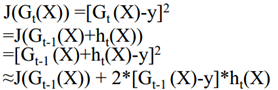 (一阶泰勒展开,因为h(x)不是单位长度,所以需要放缩到单位长度,变成有约束条件下的凸优化问题;chargeboost中试二阶展开,就不用放缩了)
(一阶泰勒展开,因为h(x)不是单位长度,所以需要放缩到单位长度,变成有约束条件下的凸优化问题;chargeboost中试二阶展开,就不用放缩了)
从集成学习器变成基学习器,不优化集成学习器整体,而以之前的学习器为已知项(G(X)),优化增加的那个学习器(损失函数也优化基学习器的)。不优化权重整体,而以之前的权重为已知项,优化权重变化的小量。每一步H(X)实际上就是CART树的生成过程。
三、Adaboost(每次新的学习器是基于上一次分类错误的样本,通过关注样本的权重来实现)
可以证明GDBT也是Adaboost的一种,最本质的区别:损失函数不同,指数损失函数:![]()
另一个区别:假设函数不同:

g(x)的取值实际上是+1,-1,然后给一个权重相加,最后只取符号,正的就是+1,负的就是-1;a会越来越小,后面的学习器会越来越弱,所以尽管后面可能有些前面的被分类错误了,影响也不大。一直经历分对,分错,分对,分错的过程,直到损失函数最小,但后面的学习器的分布权重减少。
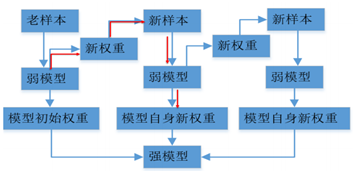
理解Adaboost训练过程
1. 新的弱模型来自于上一个弱模型,而不是之前所有模型的集合(GBDT)
2. 每个弱模型到强模型之前有权重(弱模型自身生成的权重)
3. 新权重,是样本的权重
样本权重:不同的样本分布权重对应不同训练集,类比boostrap,每一次boostrap抽样产生的新的训练集各类别样本比例不一样。(类似于上采样,多复制几遍负样本,也就是给予较多的权重)
基于错误分类的样本,给予权重的放大缩小,以使其分类正确。
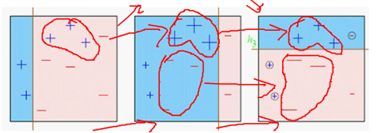
样本的权重(其实是损失函数的系数):
新的分类器必须是在上一个分类器上表现最差,与上一个分类器不一样,这样才能改进上一个学习器,否者没有什么作用,而二分类问题,表现最差的情况就是拍脑袋分类1/2概率,从而求解权重un. 这种方式求解u过麻烦,因而就有了下图中,构造一种递推的方式。


模型的权重:
误差率越小,模型权重越高,也就是说如果一个模型能把所有的都分对,那我们就给予一个很高的权重。
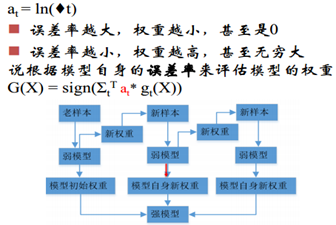

梯度下降理解Adaboost:
要求解的仍然是增加的新学习器的g(x)和模型权重at
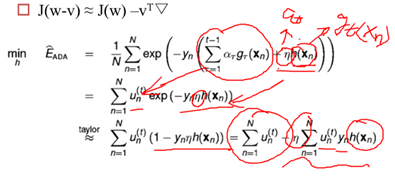
求解h(x),最优解就是h(x)=gt

求解η,最优解就是模型权重at
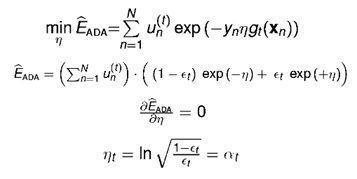
四、集成学习
精英制是加了权重之后再投票。

偏差是算法可能预测出一系列的值,取平均,与真实结果的偏离。方差是训练集数据的变化对学习结果的影响。如果说一个模型偏差高,则是欠拟合;如果说一个模型方差高,则是过拟合。一个模型的误差是由方差、偏差和噪声共同构成。

损失函数,adaboost基学习器的损失还是是0-1损失函数,只是前面加了权重,集成学习器的损失函数为指数损失函数;CART也可以看做集成学习器,看成是每一个树桩的集成学习。
