一、随机变量
可以取不同的值,不同的值有不同的概率。
看到随机变量取任何值,都要想到背后有个概率,如果是连续变量,在每一点的概率是0,连续型随机变量通常只考虑概率密度。
机器学习就是通过一堆随机变量预测另一个随机变量,先假设随机变量之间的概率分布,然后从数据中估计分布的参数。
任何概率模型的假设都是简化,不能完全刻画数据,并且每个模型都有其适用范围,比如朴素贝叶斯对于文本分类效果好。
二、贝叶斯定理
贝叶斯定理给出了从一种条件概率P(B|A)怎么推到另一种条件概率P(A|B):
![]()
这个东西有什么用呢,P(A|B)可能是个不好算的量,而P(B|A)好算,所以可以通过好算的变量推出不好算的变量。P(A) 是先验概率,P(A|B)是后验概率。
基于 总体信息+样本信息+先验信息 进行统计推断的方法和理论 称为贝叶斯统计学

传统的统计需要的样本量往往很大,而贝叶斯分析在小样本的情况下,也能得到比较准确的结论。
三、贝叶斯定理在机器学习中的应用
在机器学习中,A:未知参数/类别 B: 已知数据(层次贝叶斯中也可能是参数),如果是已知数据的话,P(B)就是个常数,不是很重要。
P(A)根据常理指定不同参数/类别的先验概率,这个数不准一般不是很要紧,一般P(B|A)会比较大。 P(B|A)模型假设的分布,指定参数A,数据B就能根据假设分布求出P(B|A)。
四、联合分布
联合分布的表格表示法,用表格把各种情况的联合概率都穷举出来,可做统计推断 ,把P(C高)的格子里的概率都加起来,然后用P(K强腿,C高)除以那个前面那个概率和。
,把P(C高)的格子里的概率都加起来,然后用P(K强腿,C高)除以那个前面那个概率和。

但这种方法需要做很大的表格,参数很多,并且需要完整的表格才可以;另外表示不了连续变量。如何改善呢?
并不是所有变量都是相关的,可以通过常识,分析变量间的关系,利用变量间独立/相关的关系,把分布分解为多个因子,由此而来著名的贝叶斯网络:可以看出这个网络之间变量的关系都是有向的,有向边:随机变量间的相关性(实质上是条件概率分布)。边的方向怎么决定了,一般是找到最自由的变量(不怎么受其他因素影响),然后找到这些变量影响了哪些因素。
每个节点和它的父节点组成因子,下图中有三个因子。联合分布分解成各因子的乘积。这个时候就可以通过知道各个因子的概率,从而知道整体所有的概率,大大简化了上面大表格的情况了。


下图中显示了,我们需要知道的各个因子的概率情况。我们可以数一数下图中有多少个参数呢,总共格子有24个,但是由于没有行的和的概率都是1,所以实际的参数只有15个,远远小于之前的全表格47个。

由此引出了贝叶斯网络的应用:
- 可以用过智商测试的值推测智商,也就是由子节点推测父节点。
- 观测变量间独立性
F只受K和Z影响
Z未知: F和C相关(通过Z “传递”相关性)
Z已知: F和C独立(C中所有能影响F的信息都已包含在Z中)
当Z已知时,可以利用此估计


五、朴素贝叶斯模型(贝叶斯公式+条件独立假设 = 朴素贝叶斯方法)
垃圾邮件分类。垃圾邮件和正常邮件的用词不同但是不可能手工指定。
目标:其实就是判断P(“垃圾邮件”|“具有某些特征”) 是否大于1/2
解决方案:纯数据驱动的方法,给两个邮件训练集,分别是垃圾邮件和正常邮件,计算垃圾邮件和正常邮件里各自的词/语句的分布,新邮件s, 估计p(s|垃圾)和p(s|正常),贝叶斯公式可算出 P(垃圾|新邮件)和P(正常|新邮件)哪个概率更大,就是属于哪个分类:
1.先分词: 邮件 s={我司,可,办理,正规,发票, 保真,增值税,发票,点数, 优惠}
2.我们需要算出的是
![]()

其中分母两者是一样的,要比较两个概率的大小,只需要求分子
分子中p(垃圾邮件)和p(正常邮件)这个是比较好求得,如果假设均匀先验概率,一般收到垃圾邮件的概率 , 那么剩下的只需要
, 那么剩下的只需要
3.条件独立假设
如果这组词在”垃圾”类下概率可分解即各个次之间相互独立=朴素贝叶斯假设(朴素贝叶斯的假设太过粗糙,比如“发票”和“增值税”经常一块出现,但还好该方法在文本挖掘中准确性较高),给定类别C情况下,每个特征独立。此时只需要算出每个词在某类中出现的概率,然后相乘,就可以得到一组词出现在垃圾邮件的概率。
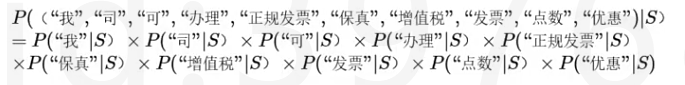


但乘法概率太小会浮点数下溢,所以转到log空间。

存在问题
1. 缺失值问题,未出现过的词,会把其他所有信息都抹杀了。为了防止此问题出现,我们在计算词频时,要给每一个词频加上一个很小的“伪计数”

古德图灵平衡(good turing)

2. 去除停用词与选择关键词
像“我”、“可”之类的词非常中性,无论其是否出现在垃圾邮件中都无法帮助判断。这些无助于我们分类的词叫做“停用词”stop words, 可以去掉。
“正规发票”、“发票”这类词如果出现的话,邮件作为垃圾邮件的概率非常大,可以作为区分垃圾邮件的“关键词”
停用词和关键词一般都提前靠人工经验指导。
3. 重复特征问题,如果重复特征 “连乘”处理,可能就会导致某一特征被放大好几次,比如下例子中“垃圾”这个词出现两次。
(1)重复特征连乘叫多项式模型。

(2) 对于重复特征只考虑一次,每个特征只考虑出现,还是没出现,这种是伯努利模型,来自伯努利 (Bernoulli) 分布,一个随机变量要么为0要么为1。

可以两种都试下,看哪个效果好。有篇论文发现,伯努利模型在词汇表小的时候性能更好,多项模型在词汇表大的时候性能更好。
(3)混合模型在计算句子概率时,不考虑重复词语出现的次数,但在统计计算词语的概率P("词语“|S)时,却考虑重复词语的出现次数。
SKlearn中有 sklearn.naive_bayes.MultinomialNB、sklearn.naive_bayes.BernoulliNB重复值处理的模型
以上过程概括起来如下:

另外,在朴素贝叶斯眼里,“我司可办理正规发票”与“正规发票可办理我司”完全相同。朴素贝叶斯失去了词语之间的顺序信息。这相当于把所有的词汇扔进一个袋子里随便搅和,贝叶斯都认为它们一样。因此这种情况也称为词袋子模型(bag of words)。Sklearn.feature_extraction.text.countvectorizer.里面参数ngram_range = (1,1)说明只取一元,一个个独立的词,ngram_range = (1,2)会考虑相邻两个词的关系,ngram_range = (1,3)会考虑三个连续词的顺序,但可能会导致稀疏化。
代码参考:
http://blog.csdn.net/qq_27396789/article/details/54836217
语料足够大的情况下,用朴素贝叶斯,不仅仅考虑一个词,而是考虑2-gram, 3gram,效果会还可以
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer(
lowercase=True,
analyzer='char_wb',
ngram_range=(1,2),#可以理解成,它不仅考虑了一个个单词还考虑了两个两个单词
max_features=1000,#保留mostcommon1000个词 保留重要度最高的前1000个词作为特征
preprocessor=remove_noise)#可以自定义降噪的函数
vec.fit(x_train)
逻辑回归与朴素贝叶斯比较:
朴素贝叶斯模型是生成式模型(相比于辨别式模型更加强大,可以做无监督,一般需要的数据量很大)中最简单的例子,而逻辑回归是辨别式模型(不假设观察是什么分布,只关心观察怎么预测类别)中最简单的例子。如果特征不独立,朴素贝叶斯会有欠拟合的情况出现。

用频率估计可能出现 为0的情况,所以要进行调整。
实际是比较购买和不购买的后验概率。
六、语言模型(N-gram,考虑各词之间联系的分类模型)
联合概率链规则公式考虑到词和词之间的依赖关系,但是比较复杂,在实际生活中没法使用,于是我们想了很多办法去近似,比如语言模型n-gram就是它的一个简化。简化后的n-gram语法比独立性假设还是强很多。

实际应用:
词性标注、垃圾邮件识别、中文分词
如果不用深度学习,统计机器翻译用到的常用库,基于统计的语言模型的工具包,5000万到1亿的模型上做效果很好(前提都是要先用jieba分词,去掉逗号那些标点,自己做预处理)
https://github.com/kpu/kenlm
http://kheafield.com/code/kenlm/
语言模型kenlm的训练及使用