Coursera 机器学习笔记（二）

主要为第三周课程内容：逻辑回归与正则化

逻辑回归(Logistic Regression)

一、逻辑回归模型引入

分类问题是指尝试预测的是结果是否属于某一个类。

• 维基百科的定义为：根据已知训练区提供的样本，通过计算选择特征参数，建立判别函数以对样本进行的分类（有监督分类）。
• 统计学习方法中定义：在监督学习中，当输出变量Y取有限个离散值时，预测问题便成为分类问题。这时，输入变量X可以是离散的，也可以是连续的。监督学习从数据中学习一个分类模型或分类决策函数，称为分类器(classifier)。分类器对新的输入进行输出的预测(prediction)，称为分类(classification)。

典型的分类问题有：判断一封邮件是否为垃圾邮件、判断有没有的乳腺癌等等。

先只讨论二元分类问题。即y为0或者1。如判断乳腺癌分类问题，我们可以试着用线性回归的方法去拟合数据，得到一条直线：

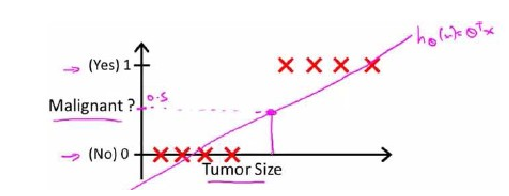
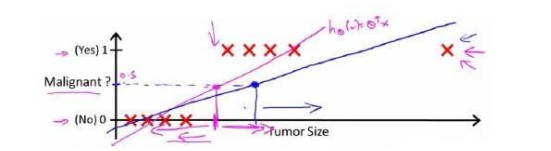
由于线性回归模型只能预测连续的值，而对于分类问题需要判断y属于0，还是1。那么可以设置一个阈值（如：0.5）来判定：

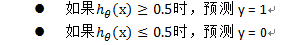
这样线性回归也能用于分类。但是缺点是如果有个异常点，会影响拟合的直线，从而原来的阈值不再合适。如图

可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

    引入一个新的模型使得模型的输出变量范围在（0,1）之间，即逻辑斯蒂回归模型，简称为逻辑回归。

    逻辑回归的假设为：h=g(θ'x)，这里引入一个新函数g，g使得h由输出范围变为（0,1）。g 称为sigmoid function 和 logistic function，表达式为：

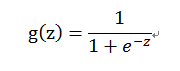
函数图像为：

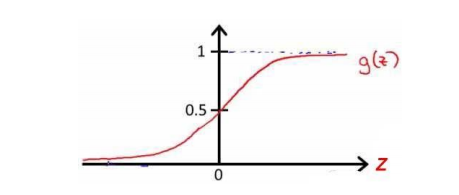
则逻辑回顾的假设也可以写成：

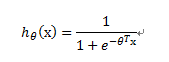
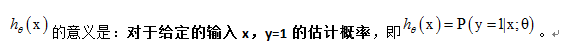
回到最初，我们仍然还可以通过设置阈值来判断，如给定的阈值为0.5：

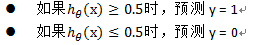
h=0.5时，z = 0，即θ'x = 0。则可以推出：

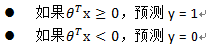
那么θ'x = 0时，可以看成是模型的判断分界线，称为判定边界，如图

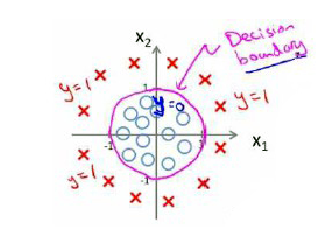
二、代价函数及其梯度下降法

如果按照线性回归模型的代价函数：模型误差的平方和，那么逻辑回归得到代价函数将是非凸函数(non-convex function)，会有很多局部最优解，将影响梯度下降法寻找全局最优解。所以需要重新定义代价函数。

重新定义的代价函数为：

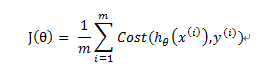
其中：

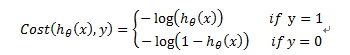
代价函数可以简写成：

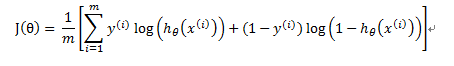
那么相应的梯度算法为：

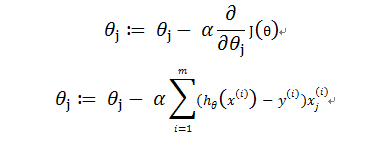
三、优化和多分类问题

　　寻找代价函数的最小值不仅仅只有梯度下降算法，还有其他的比如：共轭梯度( Conjugate Gradient )，局部优化法( Broyden fletcher goldfarb shann, BFGS) 和有限内存局部优化法(LBFGS)。

　　多分类问题即训练集里有超过2个的类，因此无法用二元变量去判断。一种解决方法是一对多方法(One-vs-All)。

　　一对多方法是将多分类转换为二元分类问题：将其中一个类标记为正类，其他类标记为分类，训练模型，得到参数，得到一个分类器。然后将第二个类标价为正类，其他类为负类，以此反复进行，得到一系列的模型参数。当需要预测时，运行所有分类器，选择其中最高值对应的模型所代表的正类。

四、正则化（Regularzation）

　　当我们训练模型的时候，通常有这三种情况：

• 得到的模型不能很好地适应训练集——低度拟合
• 得到的模型完全适应训练集，但是新输入值时，预测效果不是很好——过度拟合
• 较好地适应训练集，也能推广到新的数据。

如图：

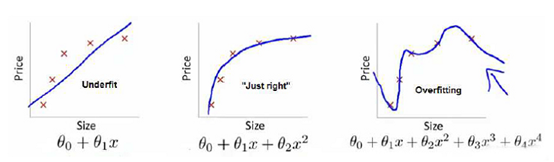
低拟合对应的是高偏差，过拟合对应的是高方差。

　　如果发生过拟合问题，应该如何处理？

　　　　方法一：丢弃一些不需要的特征

1. 人工选择
2. 算法选择（PCA等）

　　　　方法二：正则化

保留所有特征，减小参数的大小

正则化的方法是：对那些特征所需要减小的参数，在代价函数中增加相应的惩罚。如果我们有很多特征，不知道那些特征需要惩罚，那么我们可以对所有特征进行惩罚即

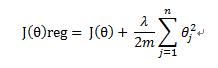
其中λ称为正则化参数，根据惯例不对进行惩罚。

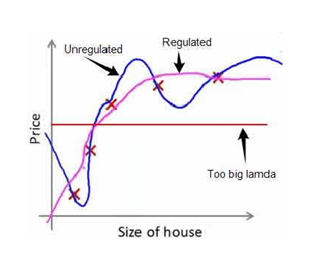
    如果λ过小，那么相当惩罚很小，造成过拟合；如果λ过大，则会所有参数都变小，导致模型接近直线，造成低度拟合;因此也需要选择适合的λ。

对线性回归正则化：

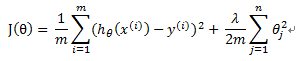
正则化后的梯度下降算法：

注意：θ0没有正则化项，其他都有。

 

对逻辑回归正则化：

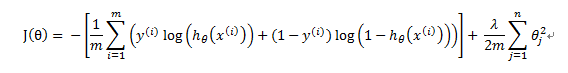
正则化后的梯度下降算法：

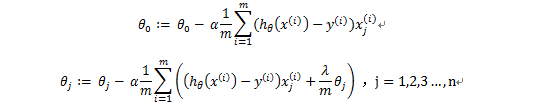
注意：虽然和线性回归一样，但是hθ(x)的表达式不一样，与线性回归不同。