一、概述
本文是根据整合网上资料与相关博文总结出来的关于【 C/C++左移右移运算符 】的知识。
二、正文
(1)结合图示篇,更加简单明了。
移位运算包含“逻辑移位”(logical shift)和“算术移位”(arithmetic shift)。
逻辑移位:移出去的位丢弃,空缺位(vacant bit)用 0 填充。
算术移位:移出去的位丢弃,空缺位(vacant bit)用“符号位”来填充,所以一般用在右移运算中。
c++中,整数分有符号数和无符号数两种,对于这两种数做左移、右移运算,稍有区别:
1、如果是无符号数,不管是左移还是右移都是“逻辑移位”
例如,分别对无符号数 179 做左移、右移操作的结果,
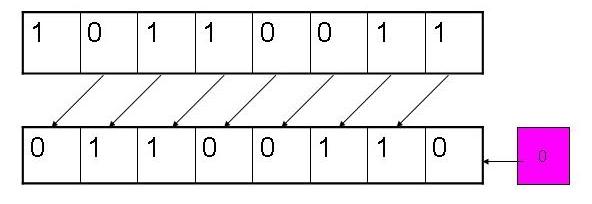
图1 逻辑左移
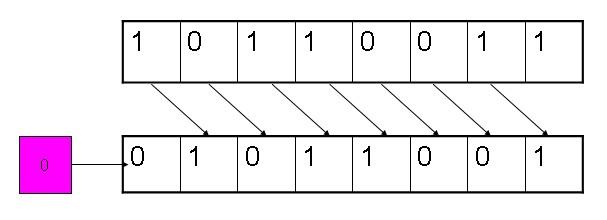
图2 逻辑右移
2、如果是有符号数,
2a,如果是做左移运算,那么做的是“逻辑移位”,同 1中无符号数的左移。
2b,如果是做右移运算,那么做的是“算术移位”。
例如:
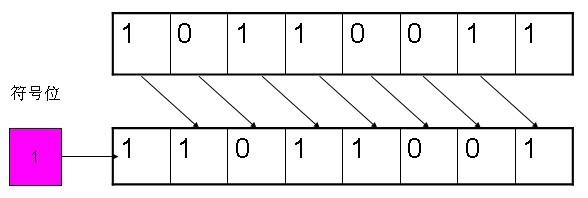
图3 负数的右移

图4 正数的右移
对于当前的大多数c/c++编译器来说,都是按照上面所讲实现的。
(2)文字描述篇,更深入。
1.左移
左移就是把一个数的所有位都向左移动若干位,在C中用<<运算符.例如:
int i = 1;
i = i << 2; //把i里的值左移2位
也就是说,1的2进制是000...0001(这里1前面0的个数和int的位数有关,32位机器,gcc里有31个0),左移2位之后变成000... 0100,也就是10进制的4,所以说左移1位相当于乘以2,那么左移n位就是乘以2的n次方了(有符号数不完全适用,因为左移有可能导致符号变化,下面 解释原因)
需要注意的一个问题是int类型最左端的符号位和移位移出去的情况.我们知道,int是有符号的整形数,最左端的1位是符号位,即0正1负,那么移位的时候就会出现溢出,例如:
int i = 0x40000000; //16进制的40000000,为2进制的01000000...0000
i = i << 1;
那么,i在左移1位之后就会变成0x80000000,也就是2进制的100000...0000,符号位被置1,其他位全是0,变成了int类型所能表 示的最小值,32位的int这个值是-2147483648,溢出.如果再接着把i左移1位会出现什么情况呢?在C语言中采用了丢弃最高位的处理方法,丢 弃了1之后,i的值变成了0.
左移里一个比较特殊的情况是当左移的位数超过该数值类型的最大位数时,编译器会用左移的位数去模类型的最大位数,然后按余数进行移位,如:
int i = 1, j = 0x80000000; //设int为32位
i = i << 33; // 33 % 32 = 1 左移1位,i变成2
j = j << 33; // 33 % 32 = 1 左移1位,j变成0,最高位被丢弃
在用gcc编译这段程序的时候编译器会给出一个warning,说左移位数>=类型长度.那么实际上i,j移动的就是1位,也就是33%32后的余数.在gcc下是这个规则,别的编译器是不是都一样现在还不清楚.
总之左移就是: 丢弃最高位,0补最低位
(2)右移
再说右移,明白了左移的道理,那么右移就比较好理解了.
右移的概念和左移相反,就是往右边挪动若干位,运算符是>>.
右移对符号位的处理和左移不同,对于有符号整数来说,比如int类型,右移会保持符号位不变,例如:
int i = 0x80000000;
i = i >> 1; //i的值不会变成0x40000000,而会变成0xc0000000
就是说,符号位向右移动后,正数的话补0,负数补1,也就是汇编语言中的算术右移.同样当移动的位数超过类型的长度时,会取余数,然后移动余数个位.
总之,在C中,左移是逻辑/算术左移(两者完全相同),右移是算术右移,会保持符号位不变.实际应用中可以根据情况用左/右移做快速的乘/除运算,这样会比循环效率高很多.