【数据结构】二叉树

表示

typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
    ElementType Data; /* 结点数据 */
    BinTree Left;     /* 指向左子树 */
    BinTree Right;    /* 指向右子树 */
};

性质

• 第i层至多有2^(i-1)个节点
• 深度为k=》至多有2^k-1个节点
• 终端节点数为n0，度为2的节点数为n2=》n0=n2+1
• 完全二叉树具有n个节点=》深度为[log2n]+1（向上取整）
• 完全二叉树按层序编号：

1. i>1，则其双亲为[i/2]（向上取整）
2. 2i>n，则i没有左孩子；否则其左孩子为2i
3. 2i+1>n，则i没有右孩子；否则其右孩子为2i+1

遍历二叉树

概念

1. 先序遍历： a、访问根节点；b、前序遍历左子树；c、前序遍历右子树。
2. 中序遍历： a、中序遍历左子树；b、访问根节点；c、中序遍历右子树。
3. 后序遍历： a、后序遍历左子树；b、后续遍历右子树；c、访问根节点。

举例

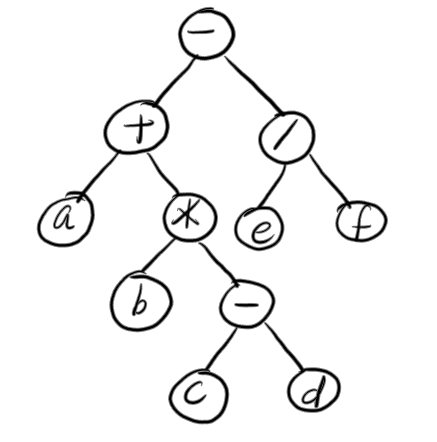
• 先序序列：-+a*b-cd/ef
• 中序遍历：a+b*(c-d)-e/f
• 后序遍历：abcde-*+ef/-
• 按层遍历：-+/a*efb-cd
• 形象的图示
  

实现

//中序遍历
void InorderTraversal( BinTree BT )
{
    if( BT ) {
        InorderTraversal( BT->Left );
        /* 此处假设对BT结点的访问就是打印数据 */
        printf("%d ", BT->Data); /* 假设数据为整型 */
        InorderTraversal( BT->Right );
    }
}
//先序遍历
void PreorderTraversal( BinTree BT )
{
    if( BT ) {
        printf("%d ", BT->Data );
        PreorderTraversal( BT->Left );
        PreorderTraversal( BT->Right );
    }
}
//后序遍历
void PostorderTraversal( BinTree BT )
{
    if( BT ) {
        PostorderTraversal( BT->Left );
        PostorderTraversal( BT->Right );
        printf("%d ", BT->Data);
    }
}
//按层遍历
void LevelorderTraversal ( BinTree BT )
{ 
    Queue Q; 
    BinTree T;
    if ( !BT ) return; /* 若是空树则直接返回 */
    
    Q = CreatQueue(); /* 创建空队列Q */
    AddQ( Q, BT );
    while ( !IsEmpty(Q) ) {
        T = DeleteQ( Q );
        printf("%d ", T->Data); /* 访问取出队列的结点 */
        if ( T->Left )   AddQ( Q, T->Left );
        if ( T->Right )  AddQ( Q, T->Right );
    }
}

还原二叉树

要已知两种遍历结果，还原一棵二叉树：前序/后序/按层+中序遍历。

也就是说，中序遍历是必要的。

本部分内容在我的另一篇博客有详细解释：https://www.cnblogs.com/fighterkaka22/p/14203479.html

波兰表达式

观察前面遍历二叉树的举例，可以发现，该三个序列分别为波兰式、正常表达式和逆波兰式。

线索二叉树

背景

当我们希望得到二叉树中某一个结点的前驱或者后继结点时，普通的二叉树是无法直接得到的，只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次，非常不方便。因此考虑，是否能够改变原有的结构，将结点的前驱和后继的信息存储进来。

原理

记ptr指向二叉链表中的一个结点，以下是建立线索的规则：

（1）如果ptr->lchild为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱；

（2）如果ptr->rchild为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继；

显然，在决定lchild是指向左孩子还是前驱，rchild是指向右孩子还是后继，需要一个区分标志的。因此，我们在每个结点再增设两个标志域ltag和rtag，注意ltag和rtag只是区分0或1数字的布尔型变量，其占用内存空间要小于像lchild和rchild的指针变量。

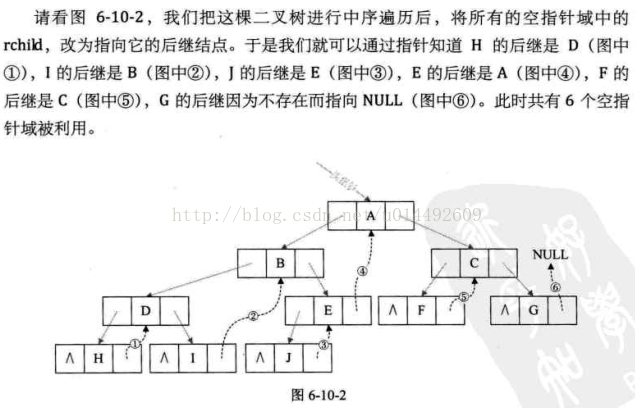
二叉树线索化

中序遍历进行二叉树线索化代码：

void InThreading(BiThrTree B,BiThrTree *pre) {
  if(!B) return;
 
  InThreading(B->lchild,pre);   
//--------------------中间为修改空指针代码---------------------
 
  if(!B->lchild){                   //没有左孩子 
    B->LTag = Thread;               //修改标志域为前驱线索
    B->lchild = *pre;               //左孩子指向前驱结点
  }
 
  if(!(*pre)->rchild){              //没有右孩子
    (*pre)->RTag = Thread;          //修改标志域为后继线索
    (*pre)->rchild = B;             //前驱右孩子指向当前结点
  }
 
  *pre = B;                         //保持pre指向p的前驱
//---------------------------------------------------------
  InThreading(B->rchild,pre);
}

遍历线索二叉树

//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
  BiThrNode *p = T->lchild;
  while(p!=T){
    while(p->LTag==Link) p = p->lchild;    //走向左子树的尽头
    printf("%c",p->data );
    while(p->RTag==Thread && p->rchild!=T) {  //访问该结点的后续结点
      p = p->rchild; 
      printf("%c",p->data );
    }
    p = p->rchild;
  }
  return OK;
}

最优二叉树（赫夫曼树）

概念

• 结点的带权路径长度：从结点到树根之间的路径长度与结点上权的乘积。

• 树的带权路径长度：所有叶子结点的带权路径长度之和。
  

• 最优二叉树（赫夫曼树）：WPL最小的二叉树。

性质

• 包含 n 个叶子结点的赫夫曼树中共有 2n – 1 个结点。
• 哈夫曼树的结点的度数为 0 或 2， 没有度为 1 的结点。
• 具有相同带权结点的哈夫曼树不惟一。

赫夫曼算法

1. 根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空。

2. 在F中选取两棵根结点权值最小的树作为左右子，构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和。
   

3. 在F中删除这两棵树,同时将新的二叉树加入F中。
   

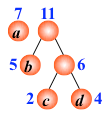
4. 重复2、3,直到F只含有一棵树为止.(得到哈夫曼树)
   

赫夫曼编码

前缀编码：任意一个字符的编码都不是另一个字符的编码的前缀。

举例：如果需传送的电文为 ‘ABACCDA‘：

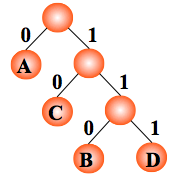
编码： A：0， C：10，B：110，D：111

任意一个叶子结点都不可能在其它叶子结点的路径中。

非二叉树

实际上，所有的树都可以通过孩子兄弟表示法表示为二叉树。