基础知识
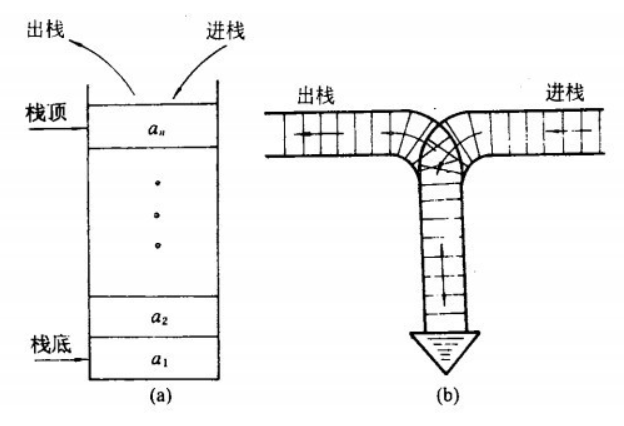
关于栈你需要知道的基础知识:
- LIFO(后进先出的线性表)
- 通常使用顺序表表示栈(方便定位)
- 常用操作:push(入栈),pop(出栈),empty(判断是否为空),top(取栈顶)
手写栈
许多情况下我们可以使用C++STL库的#include栈,但我们仍要学会手写栈。
- 初始化操作InitStack(SqStack &S)
//构造空栈S
S.base=(ElemType*)malloc(STACK_INIT_SIZE*sizeof(ElemType));
//为顺序栈动态分配存储空间
if(!S.base)exit(OVERFLOW);
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
return OK;
- 销毁栈操作DestroyStack(SqStak &S)
//若未分配栈空间
if(!S.base)return ERROR;
free(S.base);//回收栈空间
S.base=S.top=NULL;
S.stacksize=0;
return OK;
3.置空栈操作ClearStack(SqStack &S)
//若未分配栈空间
if(!S.base)return ERROR;
S.top=S.base;
return OK;
4.取栈顶元素GetTop(SqStack S,ElemType &e)
//栈空
if(S.top==S.base)return ERROR;
e=*(S.top-1);
return OK;
5.进栈操作Push(SqStack &S,ElemType e)
if ( S.top-S.base >= S.stacksize ) // 若栈满则追加存储空间
{
S.base = (ElemType * ) realloc( S.base,
( S.stacksize + STACK_INCREMENT ) * sizeof( ElemType ) );
if ( ! S. base )exit(OVERFLOW); //存储分配失败
S.top = S.base + S.stacksize;
S.stacksize += STACK_INCREMENT;
}
* S.top ++ = e;//元素e 插入栈顶,后修改栈顶指针
return OK;
6.出栈操作Pop(SqStack &S,ElemType &e)
if(S.top==S.base)return ERROR;//栈空
e=*--S.top;
return OK;
备注:
栈空:top==base
栈满:top-base==STACKSIZE
出栈序列
判断出栈序列
已知入栈序列,判断出栈序列是否正确。无论是手写判断,还是代码实现,原理均为:
- 依据给定的出栈序列,在每次将入栈序列中的元素压入栈之后尝试进行出栈(出栈直到栈顶!=即将出栈元素为止),若最终所有元素都能成功出栈(栈大小为0),则出栈序列合法。
- 代码实现中,设置一个指针,每次成功出栈后,指向下一个即将出栈的元素。
卡特兰数
一个栈进栈序列为1,2,3……n,问可能的出栈序列有多少个?
- 结论:C(2n,n)/(n+1)=(2n!)/(n!*n!)/(n+1)
- 推导:
#输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,其中:任何一个位置上之前出现的1的累计数不小于0的累计数的方案种数。
#所以有一半的方案不可行
输出序列总数目:C(2n,n)-C(2n,n+1)=C(2n,n)/(n+1)
应用
数制转换
题目:对于输入的任意一个非负十进制整数,打印输出与其等值的八进制数。
思路:计算过程是由低位到高位顺序产生八进制数的各个数位,而打印输出恰好与计算过程相反。
stack <int>S;
int N;
void conversion()
{
while(!S.empty())S.pop();
cin >> N;
while(N)
{
S.push(N%8);
N=N/8;
}
while(!S.empty())
{
cout << S.top();
S.pop();
}
}
括号匹配
题目:给定一串括号序列,判断其是否正确匹配。
思路:设置一个栈,每读入一个括号:
- 若是右括号:要么与栈顶对应的左括号抵消,要么不匹配。
- 若是左括号:入栈。
- 若栈在开始、结束时都为空,则合法匹配。
表达式求值
波兰表达式
*后续将专门开一个帖子补充。
算符优先算法
遇操作数——保存;
遇运算符号aj——与前面的刚扫描过的运算符ai比较:
- 若ai<aj 则保存aj。(因此已保存的运算符的优先关系为a1<a2<a3<a4…)
- 若ai>aj 则说明ai是已扫描的运算符中优先级最高者,可进行运算。
- 若ai=aj 则说明括号内的式子已计算完,需要消去括号。
栈与递归
汉诺塔问题
- 递归实现:
// 递归实现汉诺塔
// n 为汉诺塔圆盘编号,从小到大为 1,2,3,……
void hanoi(int n, char A, char B, char C) {
if(n == 1) {
printf("%c -> %c
", A, C); // 如果只有一个盘子,从 A 直接移动到 C
}else {
hanoi(n-1, A, C, B); // A 上的盘子,以 C 为辅助,移动到 B
hanoi(1, A, B, C); // 移动 A 上的最大的盘子到 C 上
hanoi(n-1, B, A, C); // 将 B 上的盘子以 A 为辅助,移动到 C
}
}
- 非递归实现(栈)
// 保存函数状态
struct Status {
int n;
char start, mid, end; // 初始塔,辅助中间塔,最终要移动到的塔
Status(int _n, char _A, char _B, char _C): n(_n), start(_A), mid(_B), end(_C) {}
};
// 采用非递归实现汉诺塔问题
// 由于栈的特殊性质,FILO,所以我们需要将原来函数的调用方式反过来进行
void hanoiStack(int n, char A, char B, char C) {
stack<Status> myS;
myS.push(Status(n, A, B, C));
while (!myS.empty())
{
Status ns = myS.top();
myS.pop();
if(ns.n == 1) {
printf("%c -> %c
", ns.start, ns.end);
}else {
myS.push(Status(ns.n-1, ns.mid, ns.start, ns.end));
myS.push(Status(1, ns.start, ns.mid, ns.end));
myS.push(Status(ns.n-1, ns.start, ns.end, ns.mid));
}
}
}
参考链接:
- 汉诺塔问题的非递归实现及其思考:https://www.cnblogs.com/veeupup/p/12613921.html
- 组合数学角度:https://zhuanlan.zhihu.com/p/36085324
- 处理首尾递归:https://www.cnblogs.com/blogzcan/p/7485372.html
迷宫问题
思路:从每一个位置出发,下一步都有四种选择(上右下左),先选择一个方向,如果该方向能够走下去,那么就往这个方向走,当前位置切换为下一个位置。如果不能走,那么换个方向走,如果所有方向都走不了,那么退出当前位置,到上一步的位置去,当前位置切换为上一步的位置。一致这样执行下去,如果当前位置是终点,那么结束。如果走过了所有的路径都没能到达终点,那么无解。
8皇后问题
问题:八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种计算机语言可以解决此问题。
思路:
- 从棋盘的第一行开始,从第一个位置开始,依次判断当前位置是否能够放置皇后,判断的依据为:同该行之前的所有行中皇后的所在位置进行比较,如果在同一列,或者在同一条斜线上(斜线有两条,为正方形的两个对角线),都不符合要求,继续检验后序的位置。
- 如果该行所有位置都不符合要求,则回溯(跳出这一层递归,即出栈)到前一行,改变皇后的位置,继续试探。
- 如果试探到最后一行,所有皇后摆放完毕,则直接打印出 8*8 的棋盘。最后一定要记得将棋盘恢复原样,避免影响下一次摆放。