最小乘积生成树

type
ans=record
p,q:longint;
end;
var
s,u,v,x,y:array[0..10000] of longint;
f:array[0..200] of longint;
i,j,k,n:longint;
anss,ans1,ans2:ans;
o1,o2:int64;
procedure swap(var x,y:longint);
var
w:longint;
begin
    w:=x; x:=y; y:=w;
end;
procedure sort(l,r:longint);
var
w,mid,i,j:longint;
begin
    i:=l; j:=r;
    mid:=s[(l+r) div 2];
    repeat
      while s[i]<mid do
        inc(i);
      while s[j]>mid do
        dec(j);
      if not(i>j) then
      begin
          swap(s[i],s[j]);
          swap(u[i],u[j]);
          swap(v[i],v[j]);
          swap(x[i],x[j]);
          swap(y[i],y[j]);
          inc(i);
          dec(j);
      end;
    until i>j;
    if l<j then sort(l,j);
    if i<r then sort(i,r);
end;
function find(x:longint):longint;
begin
    if f[x]=x then exit(x);
    find:=find(f[x]);
    f[x]:=find;
end;
function kl:ans;
var
t,fx,fy,i:longint;
sum:ans;
begin
    sort(1,k);
    for i:=1 to n do f[i]:=i;
    sum.p:=0; sum.q:=0; t:=0;
    for i:=1 to k do
    begin
        fx:=find(x[i]);
        fy:=find(y[i]);
        if fx<>fy then
        begin
            f[fx]:=fy;
            inc(t);
            sum.p:=sum.p+u[i];
            sum.q:=sum.q+v[i];
            if t=n-1 then
            break;
        end;
    end;
    o1:=anss.p*anss.q;
    o2:=sum.p*sum.q;
    if (o1>o2)or((o1=o2)and(anss.p>sum.p)) then
    anss:=sum;
    kl:=sum;
end;
procedure solve(a,b:ans);
var
aa,bb,cc,i:longint;
c:ans;
begin
    aa:=(a.q-b.q);   bb:=(b.p-a.p);  cc:=a.p*b.q-a.q*b.p;
    for i:=1 to k do
        s[i]:=u[i]*aa+v[i]*bb;
    c:=kl;
    if c.p*aa+c.q*bb+cc>=0 then exit;
    solve(a,c);
    solve(c,b);
end;
begin
    read(n,k);
    for i:=1 to k do
    begin
        read(x[i],y[i],u[i],v[i]);
        inc(x[i]); inc(y[i]);
    end;
    anss.p:=trunc(sqrt(maxlongint)); anss.q:=trunc(sqrt(maxlongint));
    s:=u; ans1:=kl;
    s:=v; ans2:=kl;
    solve(ans1,ans2);
    writeln(anss.p,' ',anss.q);
end.

(bzoj 2395)

一般的，这种题型会给你两个参数a[i],b[i],先分别根据以a[i]与b[i]做最小生成树，得到最靠近X轴与Y轴的点。

因为题目要求∑a[i]*∑b[j]最小，也就是反比例函数y=k/x中的k最小，我们每次可以选择离直线最远的点。

但是我刚学向量不久，还不会叉积，于是只能用点到直线距离的公式。。。

每次求出两个边界点直线的解析式 ax+by+c=0;

由(x1,y1),(x2,y2) ;

可算出a=(y1-y2); b=(x2-x1); c=x1*y2-x2*y1;

直线到点(x,y)的距离为：a*x+b*y+c/√(a^2+b^2)

所以可以算出每个点到直线的距离大小又因为与点有关的是x,y,所以只要比较(a*x+b*y)的大小再进行排序

就求出了可能更优的边，再一直递归去求可能更优的点。

但递归边界是什么呢？

当求出的最优点在直线外侧时

  

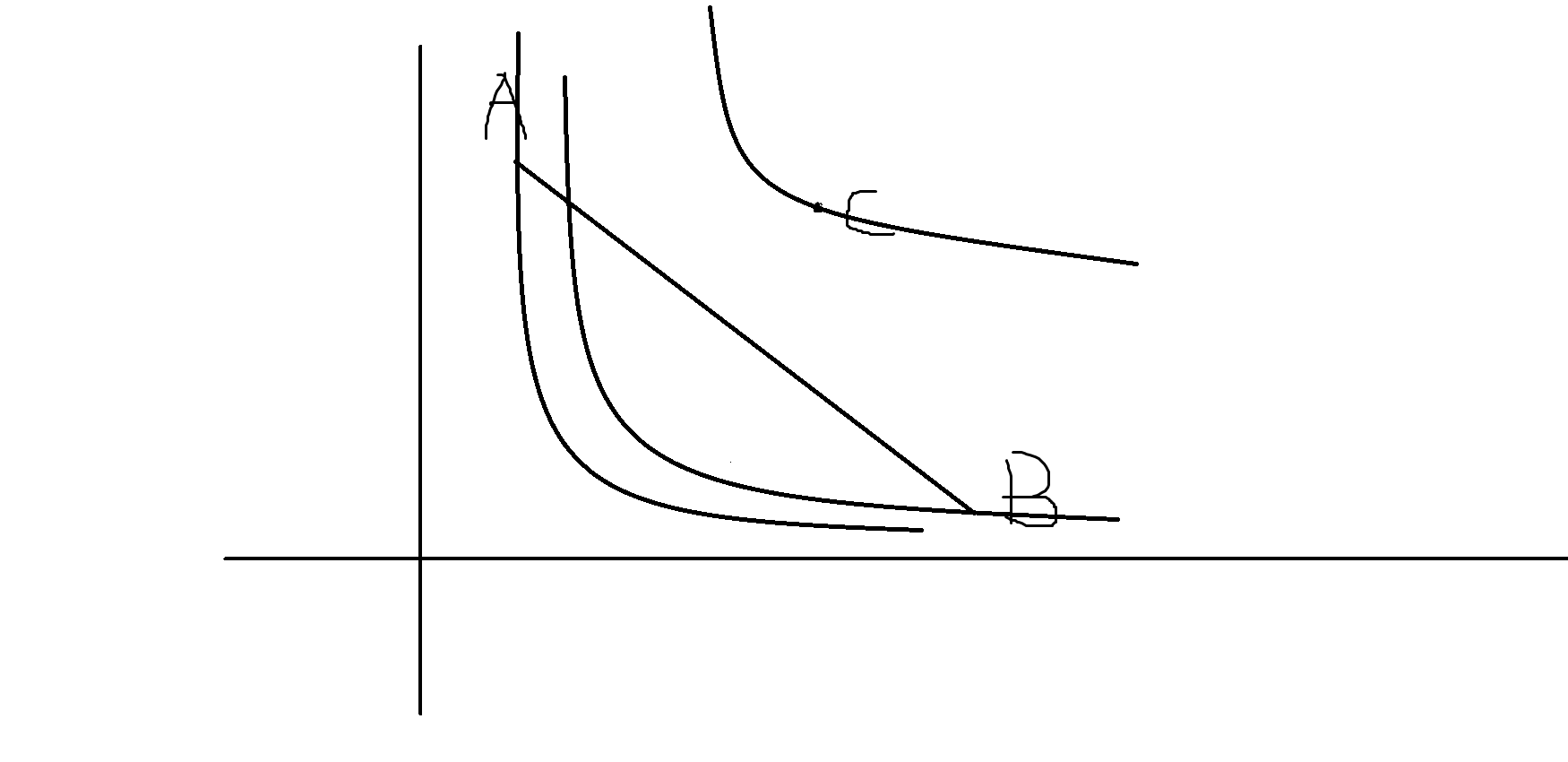
很显然，当a*x+b*y+c>=0时

这一定没有A.B优，这时就可以退出了