0.随机变量及其概率密度函数、采样的用途:
概率密度函数是用于描述某个随机变量的输出值在某个确定值附近的可能性的函数,横坐标为随机变量的某个确定值(范围为[min(值域),max(值域)]),纵坐标为可能性(范围为[0~1]) ,该函数关于z的积分和为1。
假定随机变量z服从于某个概率分布B,对应的概率密度函数是p(z)。以下将概率密度函数简称为pdf(probability density function)。
关于对随机变量z进行采样:
①什么是采样:就是通过某种特定的方法得到随机变量z的某些确定值,这些确定值组成的集合为{z(1),z(2),z(3)...z(N)},该集合里的值服从pdf为p(z)的概率分布B。
②为什么需要采样:在概率图模型/生成模型中,一般研究的对象都是随机变量,所以研究的问题常常可以转化为求解f(z)关于概率分布p(z)的期望问题。表示为求解 Ep(z)[f(z)]。而求期望问题经过下列转化往往可以转化为求解数值积分问题。

求解数值积分需要用到随机变量z的采样值z(1),z(2),...,z(N),并且z服从pdf为p(z)的分布。
其中N是采样点的个数,由于p(z)是随机变量的取值的可能性,对p(z)求积分相当于对p(z)进行采样得到的采样点的数值积分/N。
对p(z)进行采样的意义是:某个随机变量z满足pdf为p(z)的概率分布,而我们要通过某个特定的办法得到一系列的z的确定值。
由于期望的实际含义其实是包含所有可能值的z,本质还是只有一个z;而采样得到的是N个z的确定值,所以采样得到的数值积分需要*1/N。
所以求解期望问题的重点转化为解决对满足pdf为p(z)的随机变量z进行采样的问题。下面介绍几种采样方法。
1.基本的采样方法(适用于z是低维变量的情况)
①cdf采样:
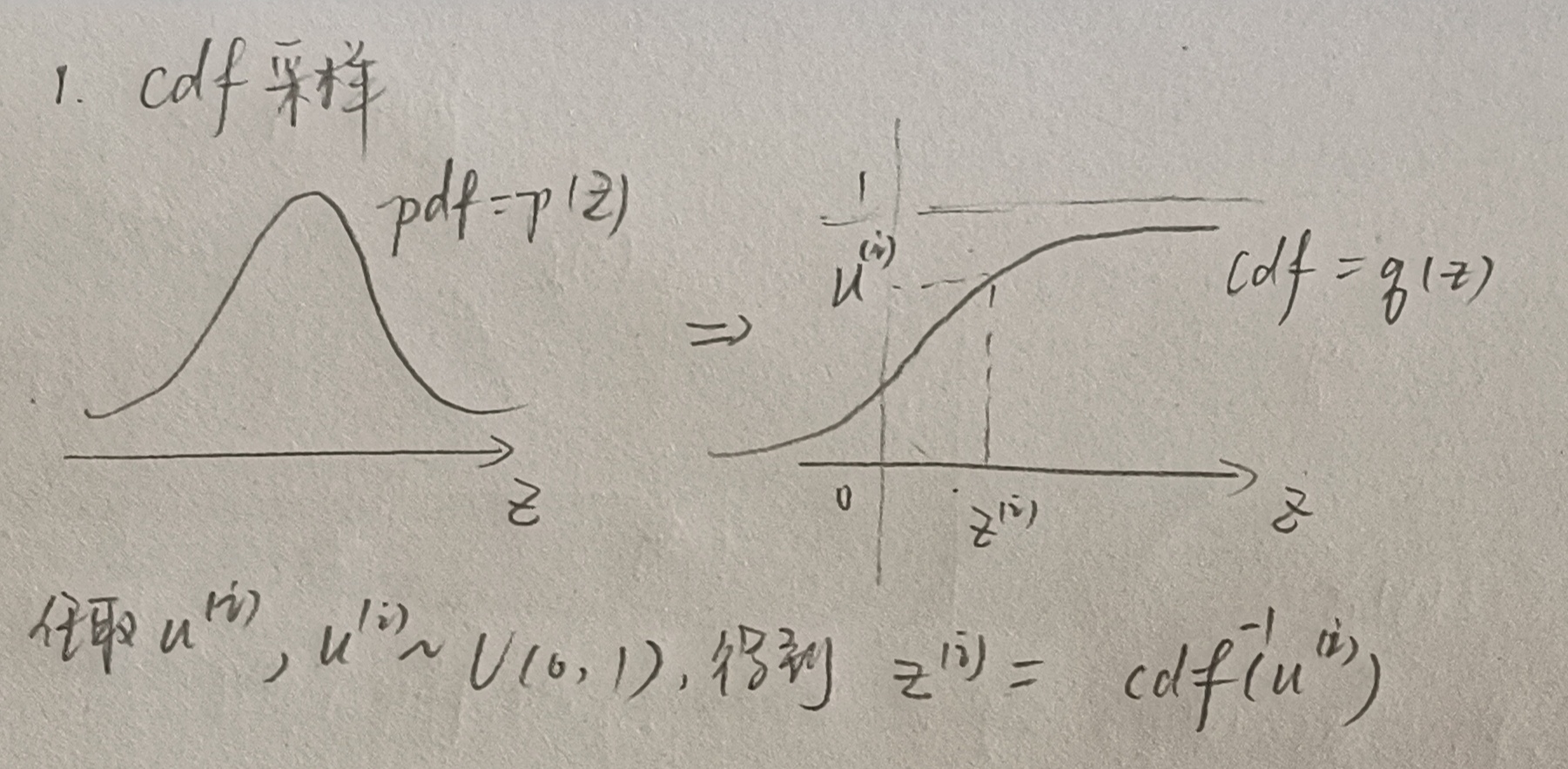
cdf的局限是:有些分布的pdf不容易找出对应的cdf,或者cdf的反函数不容易求等等。所以该采样方法只适用于比较简单的问题。
②rejection采样:

③Importance采样:
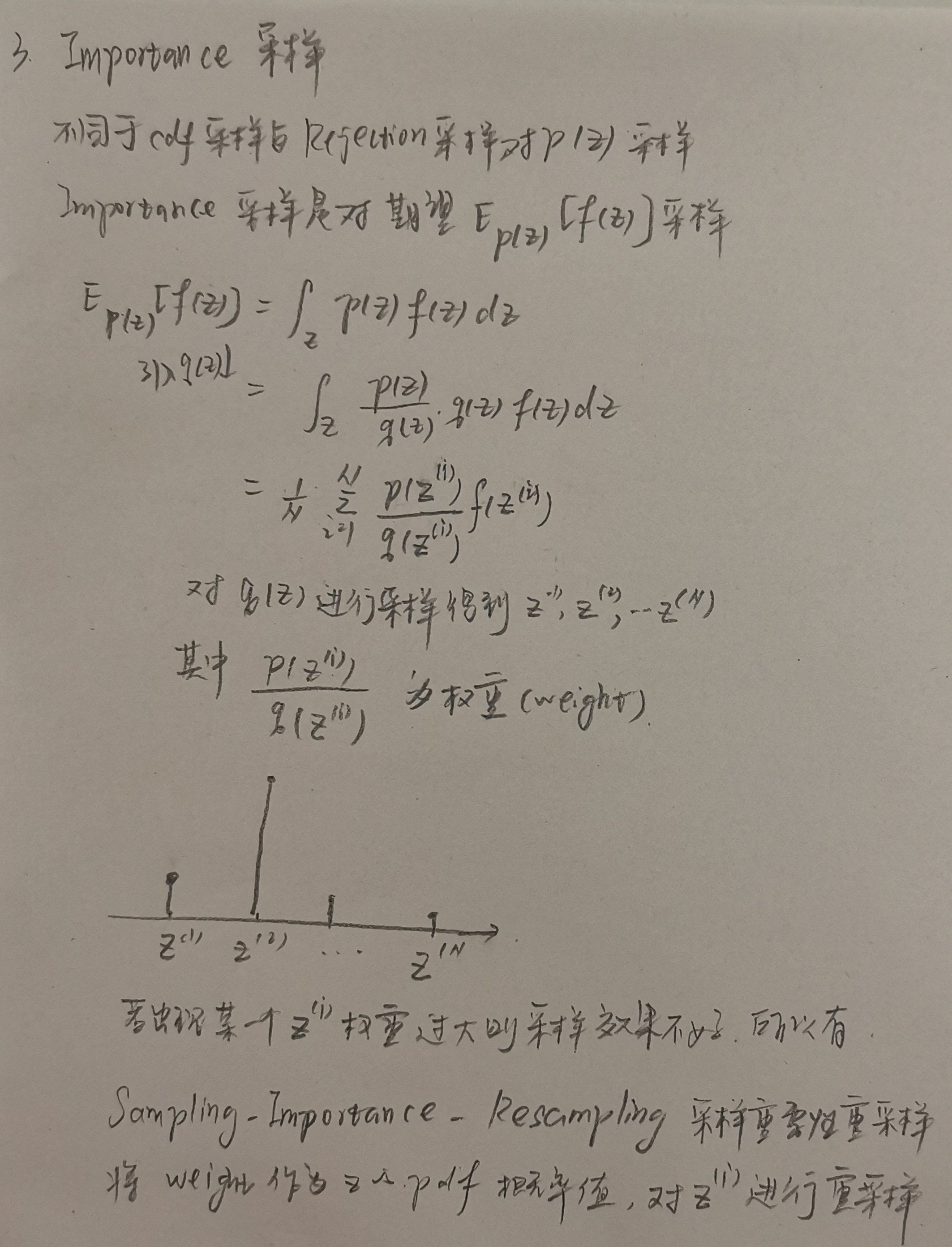
rejection采样和Importance采样的方法都强烈依赖于proposal distribution q(z) 和原始pdf p(z)的相似程度,相似程度越高,采样的效率越高。
2.Monte Carlo方法(适用于z是高维变量的情况)
Monte Carlo本质是基于采样的随机近似方法。
因为在高维空间里,因为高维空间得数据具有稀疏性,选取的q(z)如果和p(z)没有很相近,就会导致采样的效率很低,所以针对高维的随机变量z(对应的数值积分问题)的采样点获取,提出了Monte Carlo方法。
怎么随机?
怎么近似?
怎么采样?
由于markov chain的各个时刻的随机变量zt都服从于某一个概率分布p(zt),如果每个zt的边缘概率分布p(zt)都是一样的【区别于条件概率分布p(zt|zt-1)】,
那么“对概率分布p(z)采样”就等价于“得到Markov chain的每个随机变量的状态值”。每个zt都满足的概率分布p(z)有一个特殊的名字,叫做“平稳分布”。

参考资料:
1.https://www.bilibili.com/video/BV1dW411z7qs?p=1,作者:shuhuai008