简介
ARIMA： AutoRegressive Integrated Moving Average
ARIMA是两个算法的结合：AR和MA。其公式如下：
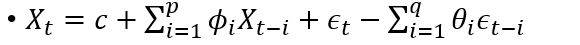
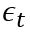是白噪声，均值为0， C是常数。 ARIMA的前半部分就是Autoregressive：
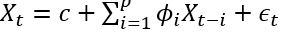， 后半部分是moving average：
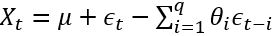。 AR实际上就是一个无限脉冲响应滤波器（infinite impulse resopnse）, MA是一个有限脉冲响应（finite impulse resopnse），输入是白噪声。
ARIMA里面的I指Integrated（差分）。 ARIMA（p,d,q）就表示p阶AR，d次差分，q阶MA。 为什么要进行差分呢？ ARIMA的前提是数据是stationary的，也就是说统计特性（mean，variance，correlation等）不会随着时间窗口的不同而变化。用数学表示就是联合分布相同：
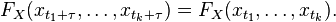
当然很多时候并不符合这个要求，例如这里的airline passenger数据。有很多方式对原始数据进行变换可以使之stationary：
（1） 差分，即Integrated。 例如一阶差分是把原数列每一项减去前一项的值。二阶差分是一阶差分基础上再来一次差分。这是最推荐的做法
（2）先用某种函数大致拟合原始数据，再用ARIMA处理剩余量。例如，先用一条直线拟合airline passenger的趋势，于是原始数据就变成了每个数据点离这条直线的偏移。再用ARIMA去拟合这些偏移量。
（3）对原始数据取log或者开根号。这对variance不是常数的很有效。
时间序列
时间序列简单的说就是各时间点上形成的数值序列，时间序列分析就是通过观察历史数据预测未来的值。在这里需要强调一点的是，时间序列分析并不是关于时间的回归，它主要是研究自身的变化规律的（这里不考虑含外生变量的时间序列）。
平稳性检验
我们知道序列平稳性是进行时间序列分析的前提条件，很多人都会有疑问，为什么要满足平稳性的要求呢？在大数定理和中心定理中要求样本同分布（这里同分布等价于时间序列中的平稳性），而我们的建模过程中有很多都是建立在大数定理和中心极限定理的前提条件下的，如果它不满足，得到的许多结论都是不可靠的。以虚假回归为例，当响应变量和输入变量都平稳时，我们用t统计量检验标准化系数的显著性。而当响应变量和输入变量不平稳时，其标准化系数不在满足t分布，这时再用t检验来进行显著性分析，导致拒绝原假设的概率增加，即容易犯第一类错误，从而得出错误的结论。
平稳时间序列有两种定义：严平稳和宽平稳
严平稳顾名思义，是一种条件非常苛刻的平稳性，它要求序列随着时间的推移，其统计性质保持不变。对于任意的τ，其联合概率密度函数满足：
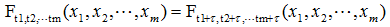
严平稳的条件只是理论上的存在，现实中用得比较多的是宽平稳的条件。
宽平稳也叫弱平稳或者二阶平稳（均值和方差平稳），它应满足：
- 常数均值
- 常数方差
- 常数自协方差
平稳性处理
由前面的分析可知，该序列是不平稳的，然而平稳性是时间序列分析的前提条件，故我们需要对不平稳的序列进行处理将其转换成平稳的序列。
对数变换
对数变换主要是为了减小数据的振动幅度，使其线性规律更加明显（我是这么理解的时间序列模型大部分都是线性的，为了尽量降低非线性的因素，需要对其进行预处理，也许我理解的不对）。对数变换相当于增加了一个惩罚机制，数据越大其惩罚越大，数据越小惩罚越小。这里强调一下，变换的序列需要满足大于0，小于0的数据不存在对数变换。
如果自相关是拖尾，偏相关截尾，则用 AR 算法
如果自相关截尾，偏相关拖尾，则用 MA 算法
如果自相关和偏相关都是拖尾，则用 ARMA 算法， ARIMA 是 ARMA 算法的扩展版，用法类似 。
时间序列分析？时间序列，就是按时间顺序排列的，随时间变化的数据序列。
生活中各领域各行业太多时间序列的数据了，销售额，顾客数，访问量，股价，油价，GDP，气温。。。随机过程的特征有均值、方差、协方差等。
如果随机过程的特征随着时间变化，则此过程是非平稳的；相反，如果随机过程的特征不随时间而变化，就称此过程是平稳的。
下图所示，左边非稳定，右边稳定。
非平稳时间序列分析时，若导致非平稳的原因是确定的，可以用的方法主要有趋势拟合模型、季节调整模型、移动平均、指数平滑等方法。
若导致非平稳的原因是随机的，方法主要有ARIMA（autoregressive integrated moving average）及自回归条件异方差模型等。什么是ARIMA？ARIMA (Auto Regressive Integrated Moving Average) 可以用来对时间序列进行预测，常被用于需求预测和规划中。可以用来对付 ‘随机过程的特征随着时间变化而非固定’ 且 ‘导致时间序列非平稳的原因是随机而非确定’ 的问题。不过，如果是从一个非平稳的时间序列开始， 首先需要做差分，直到得到一个平稳的序列。模型的思想就是从历史的数据中学习到随时间变化的模式，学到了就用这个规律去预测未来。ARIMA(p,d,q)模型，其中 d 是差分的阶数，用来得到平稳序列。AR是自回归, p为相应的自回归项。MA为移动平均，q为相应的移动平均项数。ARIMA数学模型？ARIMA（p，d，q）模型是ARMA（p，q）模型的扩展。ARIMA（p，d，q）模型可以表示为：
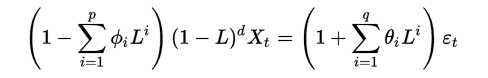
其中L 是滞后算子（Lag operator），d in Z, d>0。
AR：
当前值只是过去值的加权求和。
MA：
过去的白噪音的移动平均。
ARMA：
AR和MA的综合。
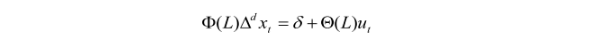
ARIMA：
和ARMA的区别，就是公式左边的x变成差分算子，保证数据的稳定性。
差分算子就是：
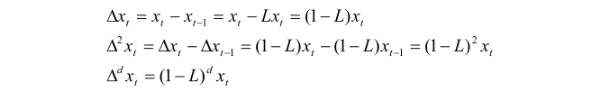
令 wt 为：
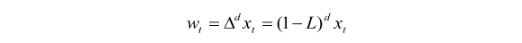
则 ARIMA 就可以写成：
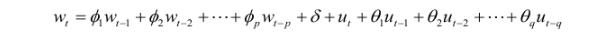
基本流程
ARIMA模型运用的基本流程有几下几步：
数据可视化，识别平稳性。
对非平稳的时间序列数据，做差分，得到平稳序列。
建立合适的模型。
平稳化处理后，若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立AR模型；
若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立MA模型；
若偏自相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。
模型的阶数在确定之后，对ARMA模型进行参数估计，比较常用是最小二乘法进行参数估计。
假设检验，判断（诊断）残差序列是否为白噪声序列。
利用已通过检验的模型进行预测。
以上为原理记录，转发而来。使用python进行ARIMA预测时，可以达到较好的效果，但是ARIMA模型非常依赖数据的时间序列的稳定性，越稳定，预测效果越好，在进行预测前的数据预处理阶段尤为重要。