从Leetcode的Combination Sum系列谈起回溯法

在LeetCode上面有一组非常经典的题型——Combination Sum，从1到4。其实就是类似于给定一个数组和一个整数，然后求数组里面哪几个数的组合相加结果为给定的整数。在这个题型系列中，1、2、3都可以通过回溯法来解决，其实4也可以，不过由于递归地比较深，采用回溯法会出现TLE。因此本文只讨论前三题。

什么是回溯法？回溯法是一种选优搜索法，按选优条件向前搜索以达到目标。当探索到某一步时，发现原先的选择并不优或达不到目标，就退回异步重新选择。回溯法是深度优先搜索的一种，但回溯法在求解过程不保留完整的树结构。

下面是原题地址：

Combination Sum：https://leetcode.com/problems/combination-sum/description/

Combination Sum II：https://leetcode.com/problems/combination-sum-ii/description/

Combination Sum III：https://leetcode.com/problems/combination-sum-iii/description/

（1）Combination Sum：

首先来看一下Combination Sum的原题：

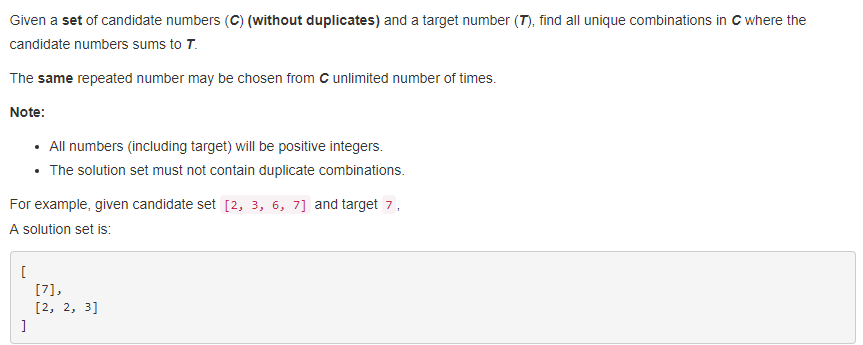
这道题目给定一个数组和一个目标数，允许数组的元素重复出现在结果中。下面是代码：

class Solution {
public:
  　　void findCombination(vector<vector<int> >& res, vector<int> candidates, vector<int> temp, int target, int pos) {
    　　　　if (target == 0) {
        　　　　res.push_back(temp);
    　　　　}
    　　　　else {
        　　　　for (int i = pos; i < candidates.size(); i++) {
            　　　　if (candidates[i] > target) break;
           　　　　 temp.push_back(candidates[i]);
            　　　　findCombination(res, candidates, temp, target - candidates[i] , i);
            　　　　temp.pop_back();
        　　　　}
    　　　　}
　　　　}

　　　vector<vector<int> > combinationSum(vector<int>& candidates, int target) {
      　　vector<int> temp;
      　　vector<vector<int> > res;
      　　sort(candidates.begin(), candidates.end());
      　　findCombination(res, candidates, temp, target, 0);
      　　return res;
　　}
};

回溯法其实很简单，基本思想就蕴含在代码中间temp.push_back、findCombination和temp.pop_back那三行。先将当前元素放到结果数组里面，然后再继续向下递归，递归完成了，将这个元素拿出来，换成下一个，继续类似的操作。谈起来有点难懂，但实际写写代码就很容易明白了。

我的习惯是写一个辅助函数来求出结果。在combinationSum函数里面很重要的一点就是要先对传入的数组进行排序。其中的原因之一是因为在辅助函数中，当加上当前循环到的candidates[i]，数组元素之和已经大于target时，我们可以马上确定停止循环，因为加上后面的元素一定是不满足条件的。还有一个原因在后面提及。

然后仔细分析这个辅助的函数几个值得注意的点。

首先我们采用的是将target减去当前candidates[i]的值，当target的值最后为零时，当前的数组就是满足条件的。为什么这样减呢？因为避免了求算结果数组的和、再和target比较的麻烦。

其次是传入的最后一个参数pos。这也是前面所谈的先对传入的数组进行排序的另外一个原因。思考一下这样一种情况：给定的数组为[1,2,3]，target为3，假若不用这个pos值，我们会同时得到[1,2]和[2,1]这两个重复的结果，这是不对的。因此，先对传入数组排序，加上pos值的应用，使后面递归要加上的元素不会包括已经访问过的元素，这样就可以避免上面情况的出现。

（2）Combination Sum II：

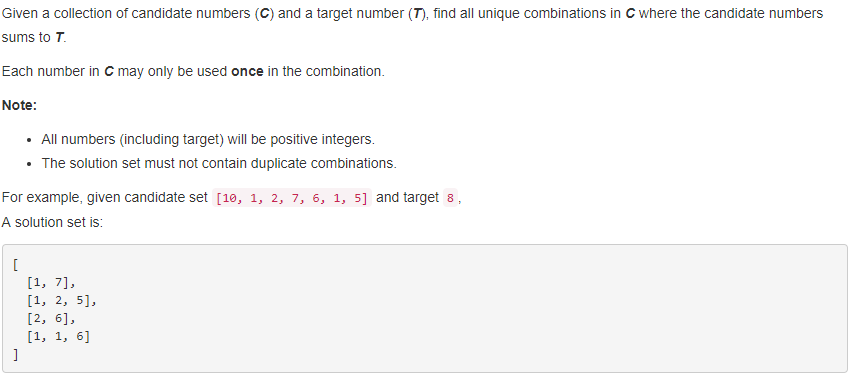
与上面一题相比，这一题不能重复已经在结果数组里面的元素。这就需要用到了一个记录数组是否已经被访问过的isVisited数组。

代码如下：

class Solution {
public:
  void dfs(vector<vector<int> >& res, map<int, bool> isVisited, vector<int> candidates, vector<int> temp, int target, int pos) {
    　　if (target == 0) {
        　　res.push_back(temp);
    　　}
    　　else {
        　　for (int i = pos; i < candidates.size(); i++) {
            　　if (!isVisited[i]) {
                　　if (target - candidates[i] < 0) break;
                　　if (i > 0 && candidates[i] == candidates[i - 1] && !isVisited[i - 1]) continue;
                　　isVisited[i] = true;
                　　temp.push_back(candidates[i]);
                　　dfs(res, isVisited, candidates, temp, target - candidates[i], i + 1);
                　　temp.pop_back();
                　　isVisited[i] = false;
            　　}
        　　}
    　　}
    }
　　vector<vector<int> > combinationSum2(vector<int>& candidates, int target) {
   　　 vector<vector<int> > res; 
   　　 map<int, bool> isVisited;
    　　for (int i = 0; i < candidates.size(); i++) {
    　　    isVisited[i] = false;
   　　 }
   　　 vector<int> temp;
   　　 sort(candidates.begin(), candidates.end());
 　　 　dfs(res, isVisited, candidates, temp, target, 0);
  　　  return res;  
　　}

};

还有一点需要注意的是（这一点可能是上面一题遗漏的，换句话来说，是出题的时候没考虑的）：样例中有两个1，考虑一下，这是不是会导致结果出现两组[1,7]？因此，我们要对这种情况进行判断，当出现这种情况时，可以马上停止往下的递归，因为之前肯定已经出现过一模一样的了。

代码中的这一段就是用来解决这种情况的（当然，要先排序）：

if (i > 0 && candidates[i] == candidates[i - 1] && !isVisited[i - 1]) continue;

当candidates[i]和前一个元素相同，且前一个元素未被访问时，跳过。我想，比较难理解的是后面的!isVisited[i - 1]。想一想，假如前面一个元素isVisited为true，那么代表这两个元素是在同一个结果里面，比如样例里面的[1,1,6]。如果是false，就说明了这两个相同的元素不在同一个结果里面，就出现重复了。

个人感觉这个小技巧可以用在所有类似题目里面。 

（3）Combination Sum III

这一题就没啥可讲了，只要明白了前面两题，这一题很容易。代码：

class Solution {
public:
  　　void helper(vector<vector<int> >& res, vector<int> temp, int k, int n, int pos) {
    　　if (temp.size() == k) {
     　　   if (n == 0) res.push_back(temp);
  　　  }
  　　  else {
     　　   for (int i = pos; i <= 9; i++) {
     　　       if (temp.size() > k || n - i < 0) break;
     　　       temp.push_back(i);
     　　       helper(res, temp, k, n - i, i + 1);
     　　       temp.pop_back();
    　　    }
   　　 }
　　}
　　vector<vector<int> > combinationSum3(int k, int n) {
   　　 vector<vector<int> > res;
   　　 vector<int> temp;
  　　  helper(res, temp, k, n, 1);    
 　　   return res;
　　}
};

上面就是Leetcode上关于回溯法的一组题目。我认为要理解回溯法，最简单的例子是求全排列，LeetCode上面也有相应的题目，因为原理差不多，直接上代码：

46. Permutations（https://leetcode.com/problems/permutations/description/）

class Solution {
public:
   void dfs(vector<vector<int> >& res, vector<int> nums, vector<int> temp, map<int, bool> isVisited, int size) {
    if (temp.size() == size) {
        res.push_back(temp);
    }
    else {
        for (int i = 0; i < size; i++) {
            if (!isVisited[i]) {
                isVisited[i] = true;
                temp.push_back(nums[i]);
                dfs(res, nums, temp, isVisited, size);
                temp.pop_back();
                isVisited[i] = false;
            }
        }
    }
}
vector<vector<int> > permute(vector<int>& nums) {
    vector<vector<int> > res;
    vector<int> begin;
    map<int, bool> isVisited;
    for (int i = 0; i < nums.size(); i++) {
        isVisited[i] = false;
    }
    dfs(res, nums, begin, isVisited, nums.size());
    return res;
}
};

47. Permutations II（https://leetcode.com/problems/permutations-ii/description/）

class Solution {
public:
    void dfs(vector<vector<int> >& res, vector<int> nums, vector<int> temp, map<int, bool> isVisited, int size) {
    if (temp.size() == size) {
        res.push_back(temp);
    }
    else {
        for (int i = 0; i < size; i++) {
            if (!isVisited[i]) {
                if (i > 0 && nums[i] == nums[i - 1] && !isVisited[i - 1]) continue;
                isVisited[i] = true;
                temp.push_back(nums[i]);
                dfs(res, nums, temp, isVisited, size);
                temp.pop_back();
                isVisited[i] = false;
            }
        }
    }
}
vector<vector<int> > permuteUnique(vector<int>& nums) {
    vector<vector<int> > res;
    vector<int> begin;
    map<int, bool> isVisited;
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size(); i++) {
        isVisited[i] = false;
    }
    dfs(res, nums, begin, isVisited, nums.size());
    return res;
}
};

这题就需要上面Combination Sum II的方法了。

还有一道也是用回溯法解决的题目，需要理解一下的，也放在这里了：

22. Generate Parentheses（https://leetcode.com/problems/generate-parentheses/description/）

class Solution {
public:
    void helper(vector<string>& res, string temp, int n, int left, int right) {
    if (left + right == 2 * n) {
        cout << temp << endl;
        res.push_back(temp);
        return;
    }
    if (left < n) {
        temp += '(';
        helper(res, temp, n, left + 1, right);
        temp = temp.substr(0, temp.size() - 1); 
    }
    if (right < left) {
        temp += ')';
        helper(res, temp, n, left, right + 1);
        temp = temp.substr(0, temp.size() - 1); 
    }
}
vector<string> generateParenthesis(int n) {
    vector<string> res;
    helper(res, "", n, 0, 0);
    return res;    
}
};