Blog:
1.Introduction of Functional Language
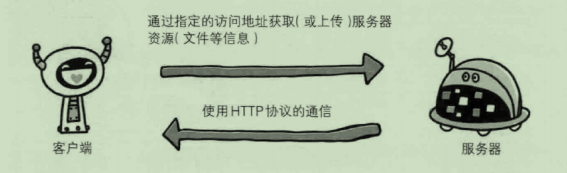
2.Analysis of HTTP
3.Comparison of URL and URI
Practice:
1.Tomcat Server installation
一、数学和函数式编程
函数式编程由Lambda演算得来,因此它与我们学过的数学非常类似。在学习函数式编程之前,我们最好忘记之前头脑中的一些编程思想(如学习C C++的时候),因为前后两个编程思维完全不同。下面分别举例来说明函数式编程中的一些概念和数学中对应概念关系:
1.函数定义
数学中要求函数必须有自变量和因变量,所以在函数式编程中,每个函数必须有输入参数和返回值。你可以看到F#中的函数不需要显示地使用关键字return去返回某个值。所以,那些只有输入参数没有返回值、只有返回值没有输入参数或者两者都没有的函数在纯函数式编程中是不存在的。
2.无副作用
数学中对函数的定义有:对于确定的自变量,有且仅有一个因变量与之对应。言外之意就是,只要输入不变,那么输出一定固定不变。函数式编程中的函数也符合该规律,函数的执行既不影响外界也不会被外界影响,只要参数不变,返回值一定不变。
3.柯里化
函数式编程中,可以将包含了多个参数的函数转换成多个包含一个参数的函数。比如对于下面的函数:
let func x y = x + y
let result = func 1 2 //result为3
可以转换成
let func x =
let func2 = fun y -> x + y
func2
let result = (func 1) 2 //result结果也为3,可以去掉括号
可以看到,一个包含两个参数的函数经过转换,变成了只包含一个参数的函数,并且该函数返回另外一个接收一个参数的函数。最后调用结果不变。这样做的好处便是:讲一个复杂的函数可以分解成多个简单函数,并且函数调用时可以逐步进行。
其实同理,在数学中也有类似“柯里化”的东西。当我们计算f(x,y) = x + y这个函数时,我们可以先将x=1带入函数,得到的结果为f(1,y) = 1 + y。这个结果显然是一个关于y的函数,之后我们再将y=2带入得到的函数中,结果为f(1,2) = 1 + 2。这个分步计算的过程其实就是类似于函数式编程中的“柯里化”。
4.不可变性
数学中我们用符号去表示一个值或者表达式,比如“令x=1”,那么x就代表1,之后不能再改变。同理,在纯函数式编程中,不存在“变量”的概念,也没有“赋值”这一说,所有我们之前称之为“变量”的东西都是标识符,它仅仅是一个符号,让它表示一个东西之后不能再改变了。
5.高阶函数
在函数式编程中,将参数为函数、或者返回值为函数的这类函数统称之为“高阶函数”,前面已经举过这样的例子。在数学中,对一个函数求导函数的过程,其实就是高阶函数,原函数经过求导变换后,得到导函数,那么原函数便是输入参数,导函数便是返回值。
二、HTTP
通过阅读本书熟悉http



三、URI and URL






四、Practice
Tomcat Server installation
1.下载tomcat,去阿帕奇官网www.apache.org

选择projects
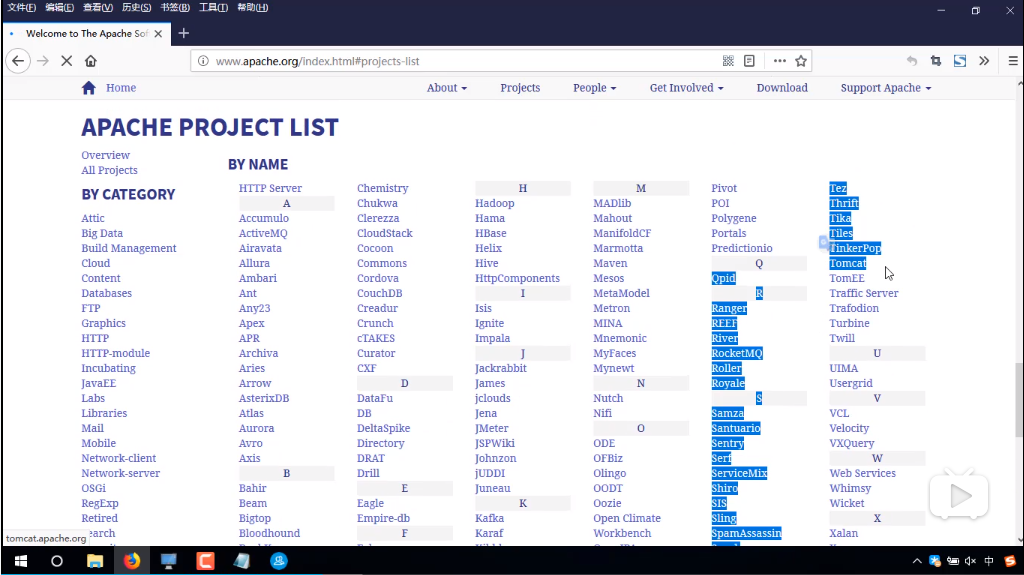
找到tomcat
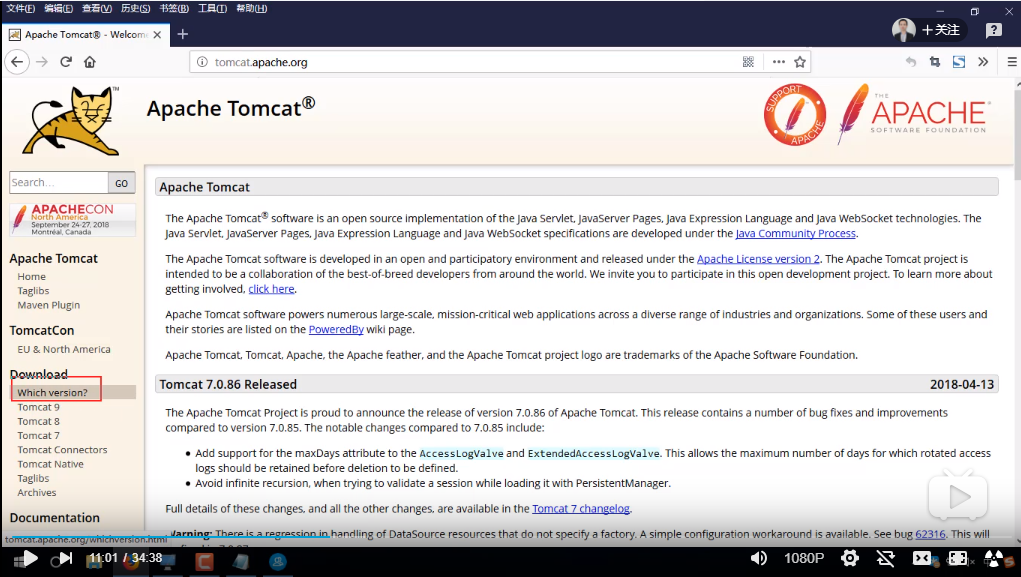
选择版本


zip一般是通用的,选择zip
2.解压
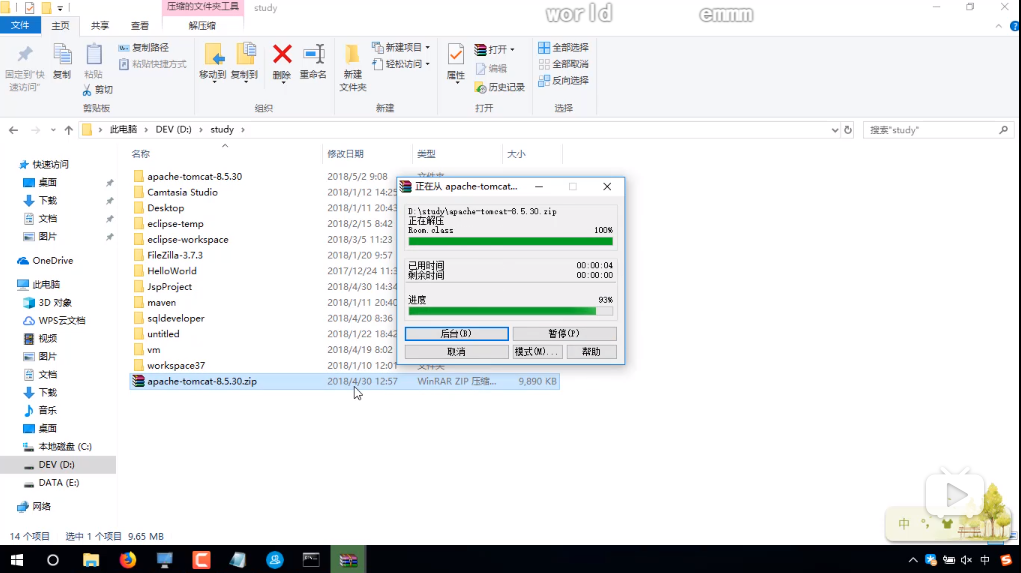
解压后的目录结构


3.配置tomcat环境变量

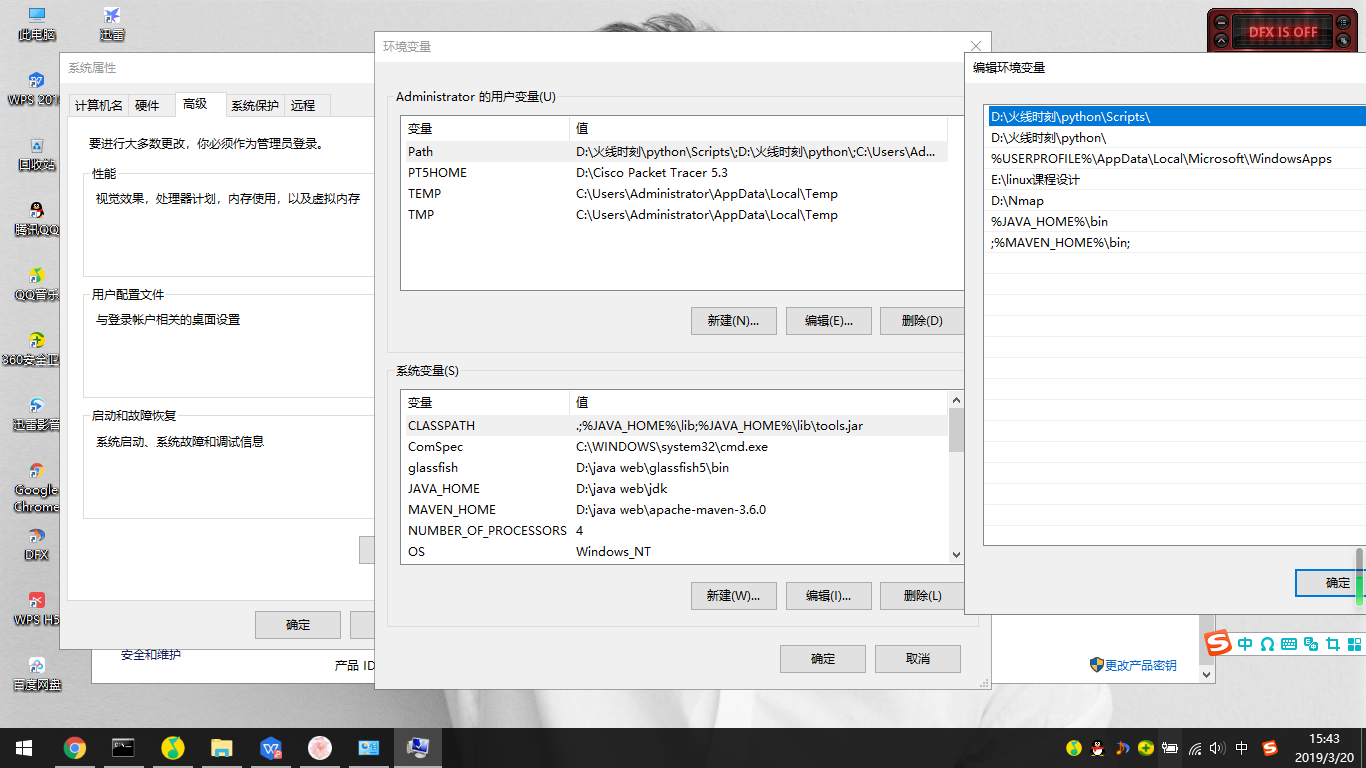

4.启动tomcat
双击bin目录下![]() 文件
文件
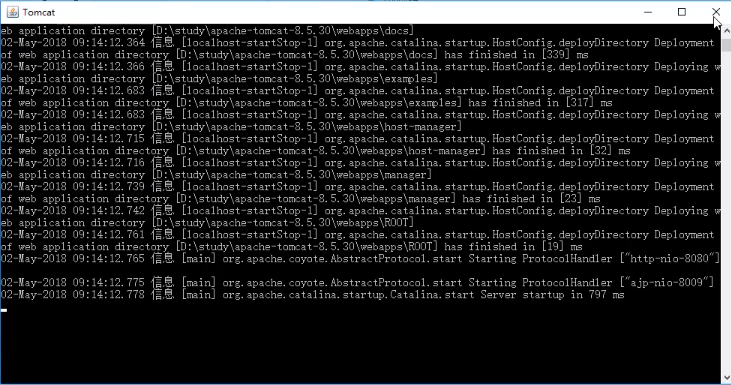
出现如上界面则启动成功
常见错误:端口号冲突
解决办法:配置文件,进入 ,
, ,
,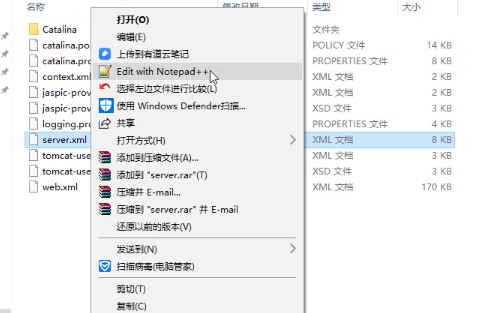
70行左右,修改8080为可以访问的端口号。

重新启动tomcat,即可。
5.访问
默认端口号8080,默认访问界面是ROOT
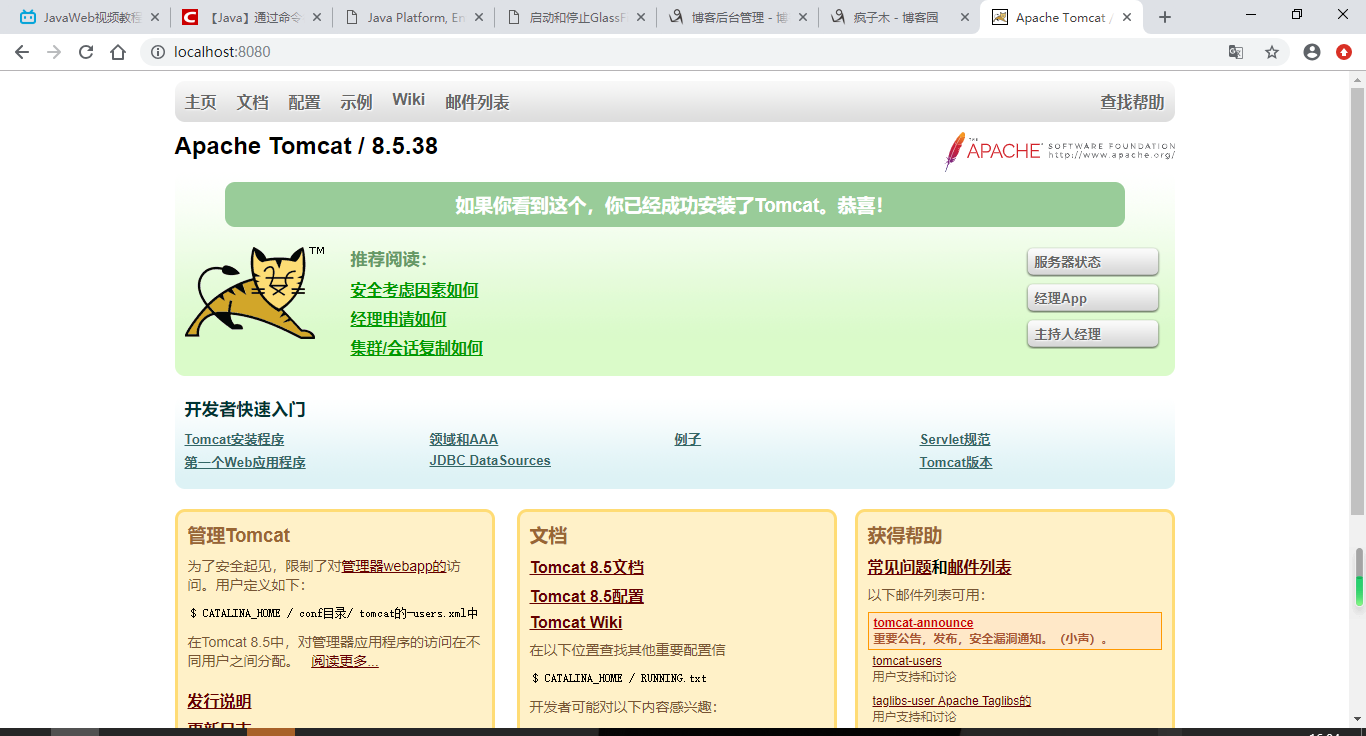
如果要访问docs文件直接在路径后加上/docs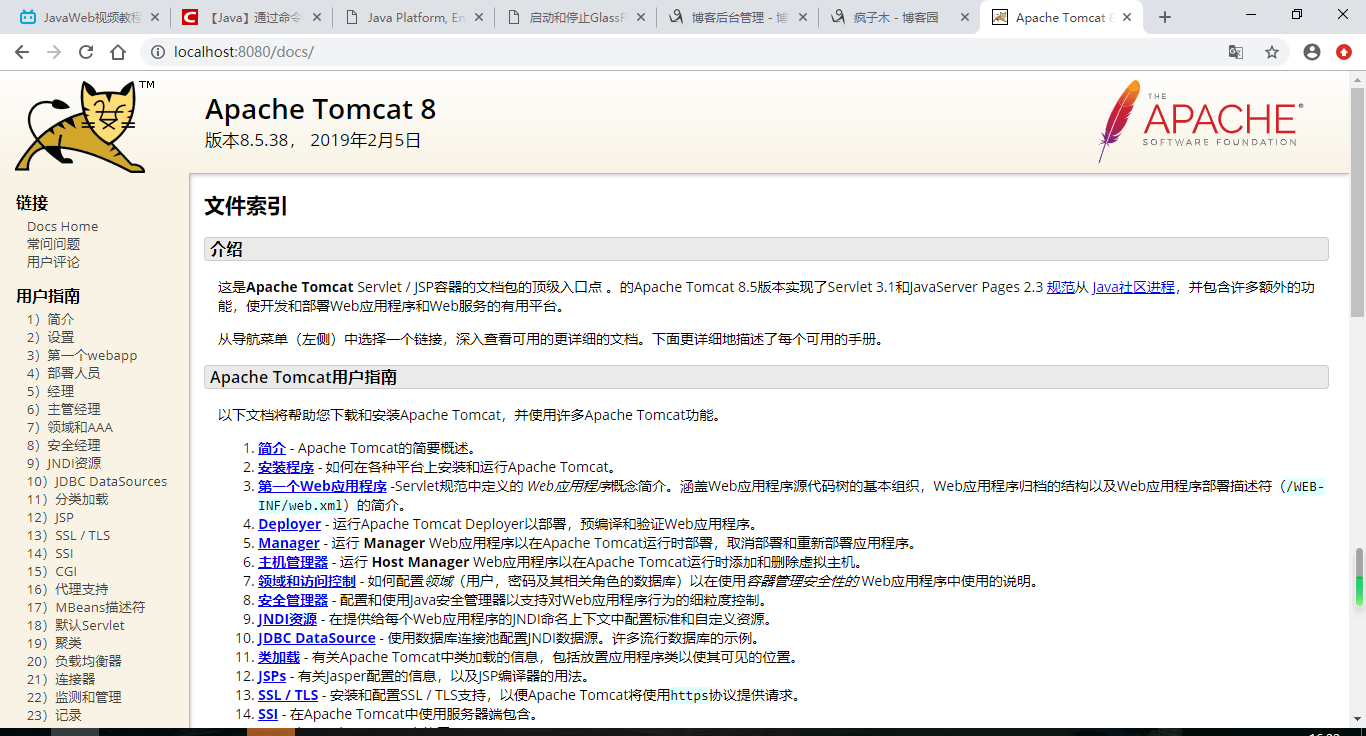
访问顺序,比如说要访问first文件

有两个index文件,为什么访问了后一个呢?
因为WEB—INF中有个配置文件 中
中
配置了访问顺序。
6.常见状态码

7.虚拟路径
a.方式一
将web项目配置到webapps以外的目录
conf/server.xml中配置
host标签中:
<Context docBase="实际路径" path="相对路径">
每次都要重启
b.方式二
D:java webapache-tomcat-8.5.38confCatalinalocalhost中新建“项目名.xml”中写入
<Context docBase="实际路径" path="相对路径">
8.虚拟主机
通过www.test.com访问本机
a.conf/server.xml

