bzoj1913 [Apio2010]signaling 信号覆盖计算几何

[Apio2010]signaling 信号覆盖

Time Limit: 20 Sec Memory Limit: 64 MB
Submit: 1661 Solved: 674
[Submit][Status][Discuss]

Description

Input

输入第一行包含一个正整数 n, 表示房子的总数。接下来有 n 行，分别表示每一个房子的位置。对于 i = 1, 2, .., n, 第i 个房子的坐标用一对整数 xi和yi来表示，中间用空格隔开。

Output

输出文件包含一个实数，表示平均有多少个房子被信号所覆盖，需保证输出结果与精确值的绝对误差不超过0.01。

Sample Input

4
0 2
4 4
0 0
2 0

Sample Output

3.500

HINT

3.5, 3.50, 3.500, … 中的任何一个输出均为正确。此外，3.49, 3.51,
3.499999，…等也都是可被接受的输出。
【数据范围】
100%的数据保证，对于 i = 1, 2, .., n, 第 i 个房子的坐标(xi, yi)为整数且
–1,000,000 ≤ xi, yi ≤ 1,000,000. 任何三个房子不在同一条直线上，任何四个房子不
在同一个圆上；
40%的数据，n ≤ 100；
70%的数据，n ≤ 500；
100%的数据，3 ≤ n ≤ 1,500。

Source

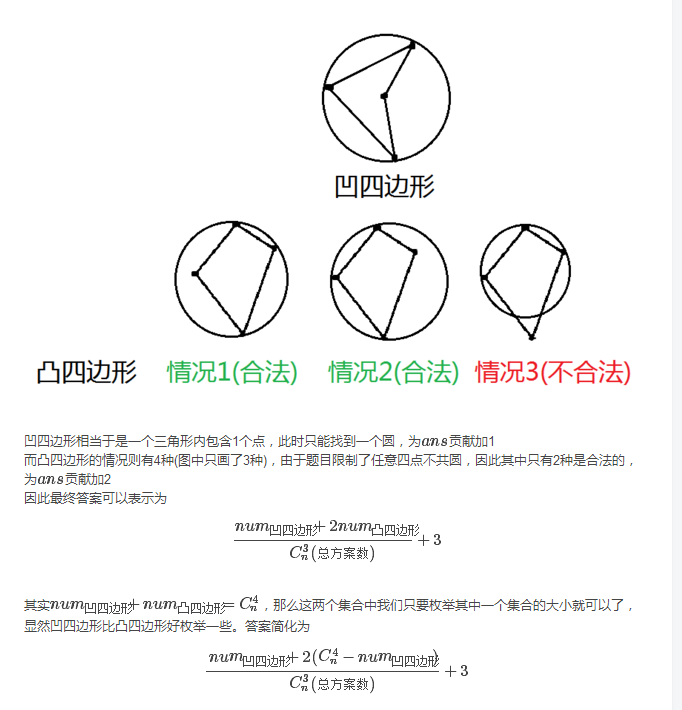
然后凹四边形怎么求，就是求三角形包涵了这个点，然后就是N^2了就好了，算上极角排序时间是n^n log n

 1 #include<cstring>
 2 #include<cmath>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<cstdio>
 6 
 7 #define N 1507
 8 #define ll long long
 9 using namespace std;
10 inline int read()
11 {
12     int x=0,f=1;char ch=getchar();
13     while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
14     while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
15     return x*f;
16 }
17 ll A,B,n;
18 struct P{
19     ll x,y;
20     double angel;
21     friend ll operator*(P a,P b){
22         return a.x*b.y-a.y*b.x;
23     }
24     friend P operator-(P a,P b){
25         return (P){a.x-b.x,a.y-b.y};
26     }
27     friend double atan2(P a){
28         return atan2(a.y,a.x);
29     }
30 }a[N],p[N];
31 
32 bool operator<(P a,P b)
33 {
34     return a.angel<b.angel;
35 }
36 ll solve(int x)
37 {
38     ll tot=(n-1)*(n-2)*(n-3)/6;
39     int top=0;
40     for(int i=1;i<=n;i++)
41     {
42         if(i!=x)p[++top]=a[i];
43         else p[0]=a[i];
44     }
45     for(int i=1;i<=top;i++)p[i].angel=atan2(p[i]-p[0]);
46     sort(p+1,p+top+1);
47     int R=2,t=0;
48     for(int i=1;i<=top;i++)
49     {
50         while((p[i]-p[0])*(p[R]-p[0])>=0)
51         {
52             R=R%top+1;t++;
53             if(R==i)break;
54         }
55         tot-=t*(t-1)/2;
56         t--;
57     }
58     return tot;
59 }
60 int main()
61 {
62     n=read();
63     if(n==3){puts("3.00");return 0;}
64     for(int i=1;i<=n;i++)
65         a[i].x=read(),a[i].y=read();
66     for(int i=1;i<=n;i++)A+=solve(i);
67     B=n*(n-1)*(n-2)*(n-3)/24-A;
68     double ans=2*B+A;
69     ans/=n*(n-1)*(n-2)/6;
70     printf("%.6lf",ans+3);
71 }

bzoj1913 [Apio2010]signaling 信号覆盖 计算几何