
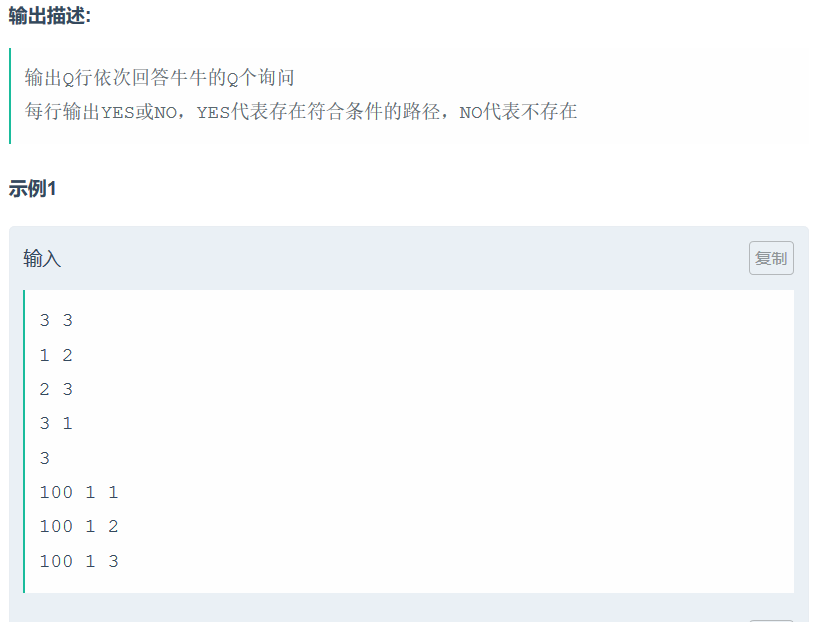
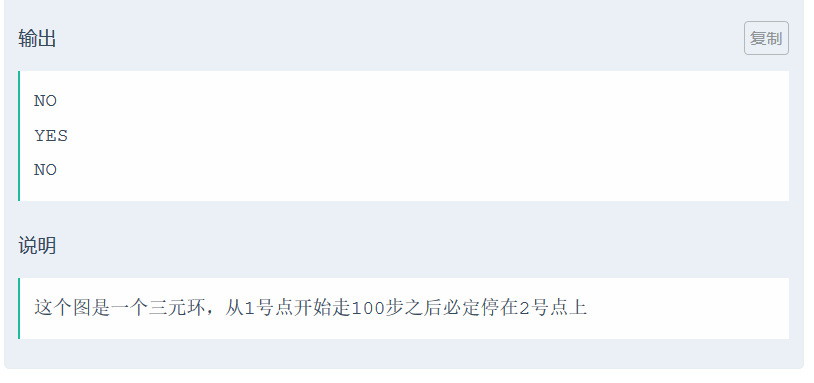
就是DP。
我们可以很简单的想到要枚举中间点,进行边数的转移。
但是因为边长数据范围很大,所以我们考虑log的倍增。
状态设计为(dp[i][j][k]),为从节点(i)走(2^k)步能否走到节点(j)。但是我们发现这样不好转移状态(其实是我不太会啊)
正解是状态压缩,但是因为(n)有点大,所以这里介绍一个黑科技:(bitset)
bitset只能存储0或1,但是较bool来说空间更优,一个元素只占一个bit,而且其中的每个元素都可以被单独访问或者修改——比如说访问s的第一位,直接(s[1])即可。
- bitset的声明:
bitset<10(长度)>s(变量名);
- bitset可以被直接赋值:
s=101;
//存储为0001100101
- bitset的输出:
cout<<s<<endl;
//0001100101
cout<<s.to_ulong()<<endl;
//101
- bitset支持位运算;
- bitset的其他功能支持:(转)
a.size() 返回大小(位数)
a.count() 返回1的个数
a.any() 返回是否有1
a.none() 返回是否没有1
a.set() 全都变成1
a.set(p) 将第p+1位变成1
a.set(p, x) 将第p+1位变成x
a.reset() 全都变成0
a.reset(p) 将第p+1位变成0
a.flip() 全都取反
a.flip(p) 将第p+1位取反
a.to_ulong() 返回它转换为unsigned long的结果,如果超出范围则报错
a.to_ullong() 返回它转换为unsigned long long的结果,如果超出范围则报错
a.to_string() 返回它转换为string的结果
之后我们就可以用bitset压位了。
状态设计为(dp[i][j][k]),(i)为走(2^i)个单位长度,(j)为出发节点,(k)为以(j)为出发节点,走(2^i)个单位长度是否能够走到其他节点的状态。(1为可以走到)
之后状态转移就是如果(dp[i][j][k]==1),那么(dp[i+1][j]|=dp[i][k])。这个是预处理节点与节点之间走多少能够到达的过程。
然后查询时另开一个新的bitset:ans来记录当前能够走到的节点,然后把(len)二进制化,显然我们从起点走,把二进制下的(len)每走一位能够到达的节点全都记录下来,然后再用它们进行转移就可以了。
代码如下:
#include<iostream>
#include<algorithm>
#include<bitset>
#include<cstdio>
#define MAXN 110
using namespace std;
int n,m,q;
bitset<MAXN>dp[40][MAXN];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
dp[0][x][y]=1;
}
for(int i=0;i<=31;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
if(dp[i][j][k])
dp[i+1][j]|=dp[i][k];
scanf("%d",&q);
while(q--)
{
int len,from,to;
scanf("%d%d%d",&len,&from,&to);
bitset<MAXN>ans;
ans.reset();
ans[from]=1;
for(int i=0;i<=31;i++)
{
if(len&(1<<i))
{
bitset<MAXN>cur;
cur.reset();
for(int j=1;j<=n;j++)
{
if(ans[j])
cur|=dp[i][j];
}
ans=cur;
}
}
if(ans[to]) printf("YES
");
else printf("NO
");
}
return 0;
}