这个题是一个比较有难度的图论+搜索题。
当然部分分还是很好拿的,我们可以跑一个比较裸的搜索,记录空白格子现在的位置、起始点的位置,然后模拟题意跑搜索。空白格子四面搜索,如果可以走的话就继续往前走,如果遇到起始点的话就把它和起始点的位置相交换。
我写丑了......只有50分,其他的大佬说暴力应该是有70分的......(以下是代码,框架来自soul_M),其实按照bfs的特性遇到第一个答案就应该结束了的,但是不知道为什么写return就WA掉了。。。如果有哪个dalao知道请私信我谢谢。qwq
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
int n,m,Q;
int ex,ey,sx,sy,tx,ty,ans;
struct Node{int x1,y1,x2,y2,sum;};
int a[50][50],f[50][50][50][50];
int move_x[5]={0,0,1,-1};
int move_y[5]={-1,1,0,0};
queue<Node>q;
inline void bfs(){
q.push((Node){ex,ey,sx,sy,0});
while(!q.empty()){
Node now=q.front();
q.pop();
int x1=now.x1;
int y1=now.y1;
int x2=now.x2;
int y2=now.y2;
int sum=now.sum;
if(sum>ans) continue;
if(f[x1][y1][x2][y2]<sum) continue;
f[x1][y1][x2][y2]=sum;
if((x2==tx) && (y2==ty)){
ans=min(ans,sum);
continue;
}
for(register int i=0;i<4;i++)
{
int cur_x1=x1+move_x[i];
int cur_y1=y1+move_y[i];
if(!a[cur_x1][cur_y1]||!a[x2][y2]) continue;
if(cur_x1<1||cur_x1>n||x2<1||x2>n) continue;
if(cur_y1<1||cur_y1>m||y2<1||y2>m) continue;
if(cur_x1==x2&&cur_y1==y2)
{
q.push((Node){x2,y2,x1,y1,sum+1});
continue;
}
q.push((Node){cur_x1,cur_y1,x2,y2,sum+1});
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&Q);
for(register int i=1;i<=n;i++)
for(register int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
while(Q--)
{
ans=0x3f3f3f3f;
memset(f,0x3f,sizeof(f));
scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);
f[ex][ey][sx][sy]=0;
bfs();
if(ans==0x3f3f3f3f) ans=-1;
printf("%d
",ans);
}
return 0;
}
(imone dalao:"暴力明明有80分的好不好!!)
现在我们考虑正解。
我们可以发现,之所以会T,原因是我们使用了过多无用的状态(也就是让空白格子在图上瞎跑)。但是我们需要的状态其实不多。为了能让空白格子推着起始点跑,空白格子是必须在起始点旁边的。
那么我们现在就知道什么是有用状态了:即在起始点周围(即上下左右四个方向)。状态的转移呢?——这个分两种,一种是从起始点周围转移到周围的另外一个位置,这个步数可以用一个bfs计算,另外一种是和起始点交换位置,步数很显然是1。
接下来的难点是如何记录状态。因为我们把起始点在棋盘中的每个位置和它上下左右的情况都抽离出来了,所以我们可以开一个(cnt)数组,(cnt[i][j][k])表示起始点在(i,j)的位置,空白格子在它周围的k(从0到3编号)位置。
之后就是后继状态的转移,我们可以考虑通过连边的方式,把合法状态和它的后继状态连起来,这样状态就有传递性和连续性了。
具体我们可以通过下面这张图来理解:
图中模拟的是目标节点和空格(假设空格在目标节点的左边)进行交换(从绿色状态转移到黄色状态)。
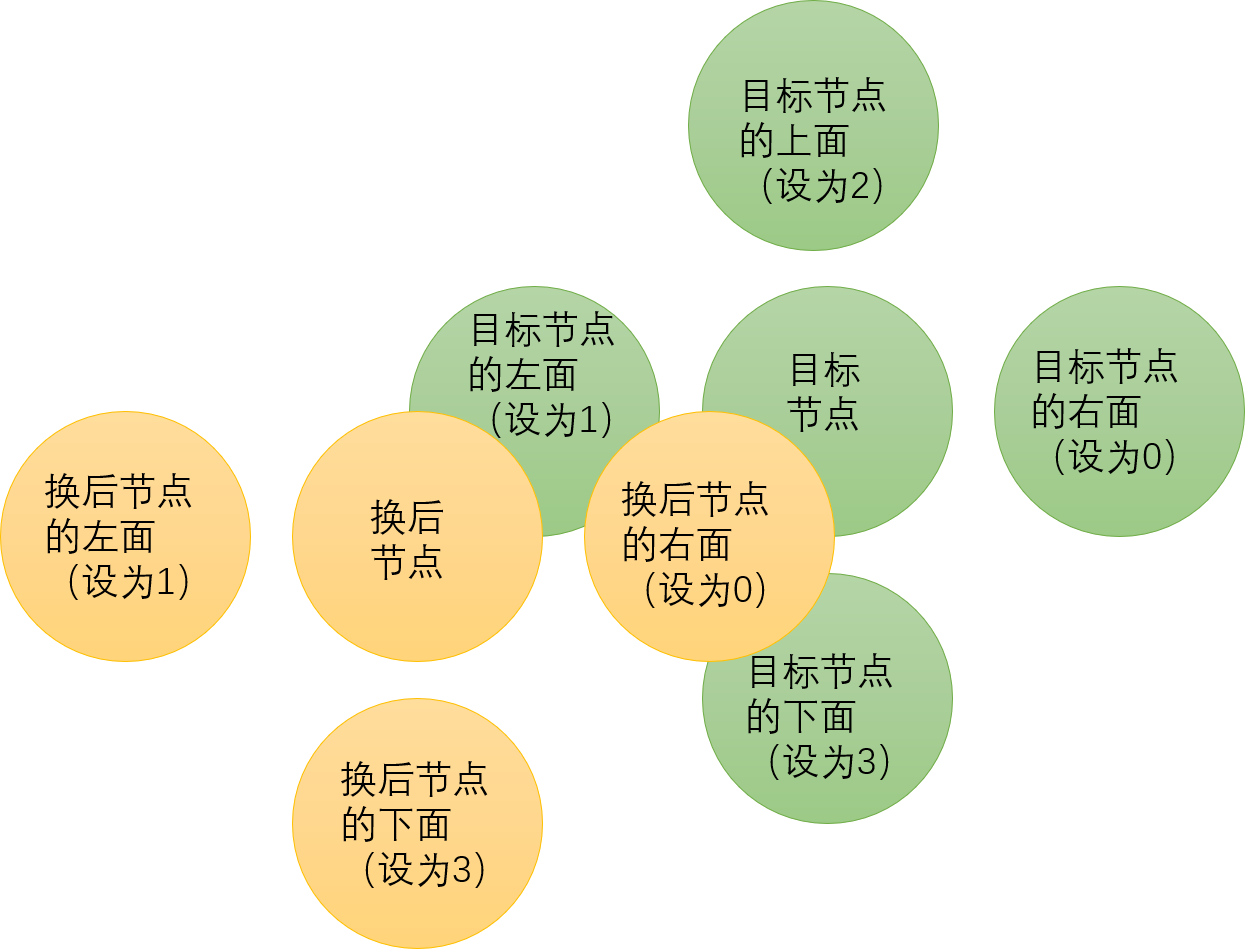
按照上面的说法,目标节点和它周围的状态是有长度为1的有向边的,它的周围状态之间也是有bfs出的长度的有向边的。
我们易知黄色“换后节点”和绿色的“目标节点的左面”的坐标其实是一样的,绿色的“目标节点”和黄色的“换后节点的右面”坐标也是一样的。但要注意的是它们记录的状态不一样,所以图还不是连通的。交换了空格与起始点的位置后,按照上图就是将绿色的“目标节点的左面”和黄色的“换后节点的右面”连一条有向边。
连完边之后spfa跑最短路就可以了。。。
但是需要注意的一点就是可能开始空白格子和起始点位置离得很大,因为我们需要空白格子推着起始点移动,所以我们开始要把空白各自移动到起始点周围。(也就是上下左右)这个用bfs求最少步数就可以了。
移动到空白格子周围就起点到终点连通了,直接最短路跑一遍就可以了。
最后我们把(cnt[endx][endy][k](0<=k<=3))的最小值记为ans。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
#include<algorithm>
#define MAXN 1234
using namespace std;
int n,m,q,edge_number,tot,ans=0x3f3f3f3f;
int a[40][40],head[MAXN*MAXN+10],dis[MAXN*MAXN+10],done[MAXN*MAXN+10];
int vis[40][40],cnt[40][40][5];
int move_x[5]={1,-1,0,0};
int move_y[5]={0,0,1,-1};
struct Edge{int nxt,to,dis;}edge[MAXN*MAXN+10];
struct Node{int x,y,len;};
inline void add(int from,int to,int dis)
{
edge[++edge_number].dis=dis;
edge[edge_number].nxt=head[from];
edge[edge_number].to=to;
head[from]=edge_number;
}
inline int bfs(int ax,int ay,int bx,int by,int cx,int cy)
{
if(ax==bx&&ay==by) return 0;
memset(vis,0,sizeof(vis));
queue<Node>q;
q.push((Node){ax,ay,0});
vis[ax][ay]=1;
while(!q.empty())
{
Node cur=q.front();
q.pop();
if(cur.x==bx&&cur.y==by) return cur.len;
for(int i=0;i<4;i++)
{
int x=cur.x+move_x[i];
int y=cur.y+move_y[i];
if(x<1||x>n||y<1||y>m) continue;
if(x==cx&&y==cy) continue;
if(vis[x][y]||!a[x][y]) continue;
q.push((Node){x,y,cur.len+1});
vis[x][y]=1;
}
}
return 0x3f3f3f3f;
}
inline int spfa(int ax,int ay,int bx,int by,int cx,int cy)
{
queue<int>q;
if(bx==cx&&by==cy) return 0;
memset(dis,0x3f,sizeof(dis));
for(int k=0;k<4;k++)
{
if(cnt[bx][by][k])
{
dis[cnt[bx][by][k]]=bfs(ax,ay,bx+move_x[k],by+move_y[k],bx,by);
q.push(cnt[bx][by][k]);
done[cnt[bx][by][k]]=1;
}
}
while(!q.empty())
{
int u=q.front(); q.pop(); done[u]=0;
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].dis)
{
dis[v]=dis[u]+edge[i].dis;
if(!done[v])
{
q.push(v);
done[v]=1;
}
}
}
}
for(int k=0;k<4;k++)
if(cnt[cx][cy][k])
ans=min(ans,dis[cnt[cx][cy][k]]);
if(ans==0x3f3f3f3f) return -1;
else return ans;
}
inline void init()
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=0;k<4;k++)
if(a[i][j]&&a[i+move_x[k]][j+move_y[k]])
cnt[i][j][k]=++tot;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=0;k<4;k++)
if(cnt[i][j][k])
add(cnt[i][j][k],cnt[i+move_x[k]][j+move_y[k]][k^1],1);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=0;k<4;k++)
for(int p=0;p<4;p++)
if(k!=p&&cnt[i][j][k]&&cnt[i][j][p])
add(cnt[i][j][k],cnt[i][j][p],bfs(i+move_x[k],j+move_y[k],i+move_x[p],j+move_y[p],i,j));
}
int main()
{
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
init();
while(q--)
{
int blank_x,blank_y,st_x,st_y,end_x,end_y;
ans=0x3f3f3f3f;
scanf("%d%d%d%d%d%d",&blank_x,&blank_y,&st_x,&st_y,&end_x,&end_y);
printf("%d
",spfa(blank_x,blank_y,st_x,st_y,end_x,end_y));
}
return 0;
}