5-1
输入一个正整数 n (1≤n≤10)和n 阶方阵a的元素，如果方阵a中的所有元素都沿主对角线对称，输出“Yes”, 否则，输出“No”。主对角线为从矩阵的左上角至右下角的连线，方阵a中的所有元素都沿主对角线对称指对所有i, k，a[i][k]和a[k][i]相等。输入输出示例如下：
输入：
3
1 2 3
4 5 6
7 8 9
输出：
No
#include <stdio.h>
int main(void)
{
int found, i, k, n;
int a[10][10];
scanf ("%d", &n);
for (i = 0; i < n; i++)
for (k = 0; k < n; k++)
scanf("%d", &a[i][k]);
found = 1;
for (i = 0; i < n; i++){
for (k = 0; k < i; k++){
if (
a[i][k]!=a[k][i]
(3分)) {
found=0
;
break;
}
}
if (
found==0
){
break;
}
}
if (found != 0){
printf("Yes
");
}
else{
printf("No
");
}
return 0;
}
7-2 选择法排序 （20 分)
本题要求将给定的n个整数从大到小排序后输出。
输入格式：
输入第一行给出一个不超过10的正整数n。第二行给出n个整数，其间以空格分隔。
输出格式：
在一行中输出从大到小有序的数列，相邻数字间有一个空格，行末不得有多余空格。
输入样例：
4
5 1 7 6
输出样例：
7 6 5 1
实验代码：
#include<stdio.h>
int main (void)
{
int i,n,m,index,z;
int a[10];
scanf("%d",&n);
for(i=0;i<n;i++){
scanf("%d",&a[i]);
}
for(m=0;m<n-1;m++){
index=m;
for(i=m+1;i<n;i++)
if(a[i]>a[index])
index=i;
z=a[index];
a[index]=a[m];
a[m]=z;
}
printf("%d",a[0]);
for(i=1;i<n;i++)
printf(" %d",a[i]);
return 0;
}
实验思路：根据书上的选择排序思想将数组先遍历一遍然后选出最大的值与设置的值进行互换。
思维导图：
实验所遇问题：没有考虑输出格式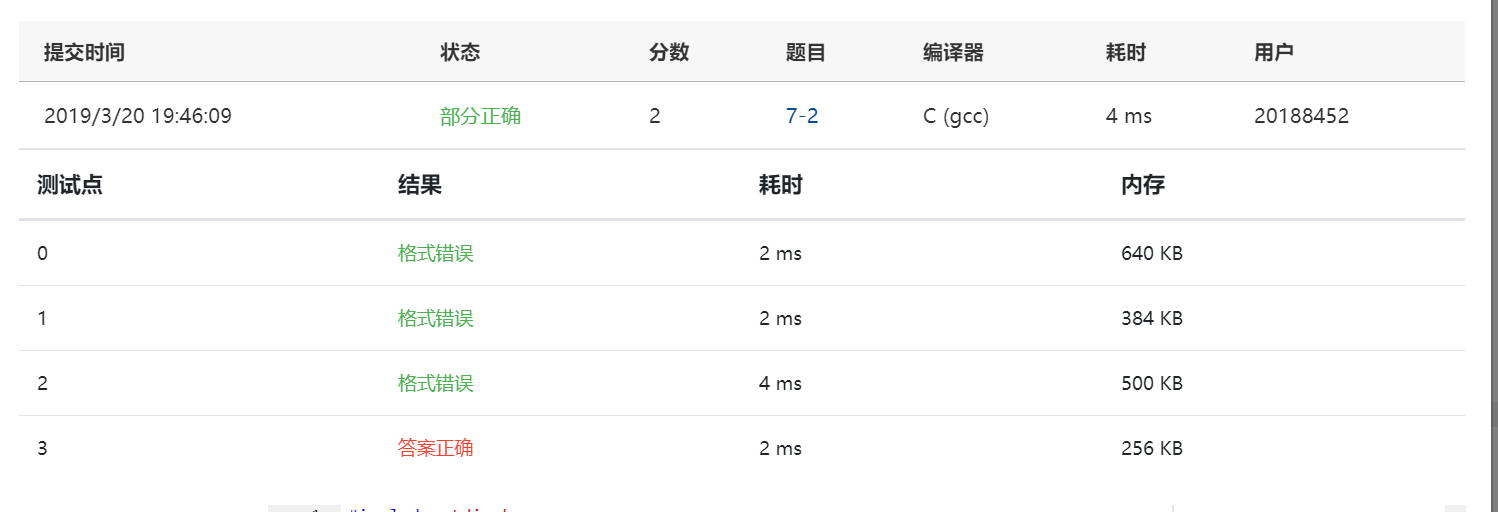
解决方法：重新审查了下题目将输出加入前空格和后空格进行尝试；然后将第一个数独自输出，然后在输出前加上空格。
正确结果截图：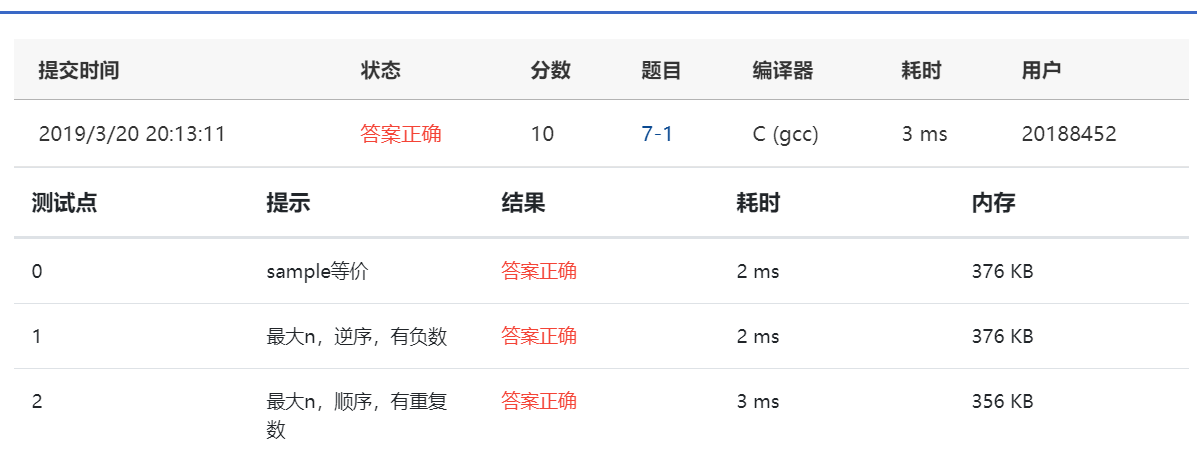
7-1 冒泡法排序 （10 分)
输入1个正整数n（1<=n<=10），然后输入n个整数并存放在数组中，将这n个整数从大到小排序后输出，相邻数字间有一个空格，行末不得有多余空格。
输入格式:
输入第一行给出一个不超过10的正整数n。第二行给出n个整数，其间以空格分隔。
输出格式:
在一行中输出从大到小有序的数列，相邻数字间有一个空格，行末不得有多余空格。
输入样例:
4
75 71 77 76
77 76 75 71
实验代码：
输出样例:
#include<stdio.h>
int main (void)
{
int i,n,m,j,temp,in;
int a[10];
scanf("%d",&n);
for(m=0;m<n;m++){
scanf("%d",&a[m]);
}
for(i=0;i<n-1;i++){
in=1;
for(j=0;j<n-1-i;j++){
if(a[j]<a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
in=0;
}
}
if(in)
break;
}
printf("%d",a[0]);
for(i=1;i<n;i++){
printf(" %d",a[i]);
}
return 0;
}
实验思路：首先在网上搜冒泡法的内容：从数组头部开始，不断比较相邻的两个元素的大小，让较大的元素逐渐往后移动（交换两个元素的值），直到数组的末尾。经过第一轮的比较，就可以找到最大的元素，并将它移动到最后一个位置。
第一轮结束后，继续第二轮。仍然从数组头部开始比较，让较大的元素逐渐往后移动，直到数组的倒数第二个元素为止。经过第二轮的比较，就可以找到次大的元素，并将它放到倒数第二个位置。
以此类推，进行 n-1（n 为数组长度）轮“冒泡”后，就可以将所有的元素都排列好。明确它的算法思想后在源代码的基础上进行修改。
思维导图：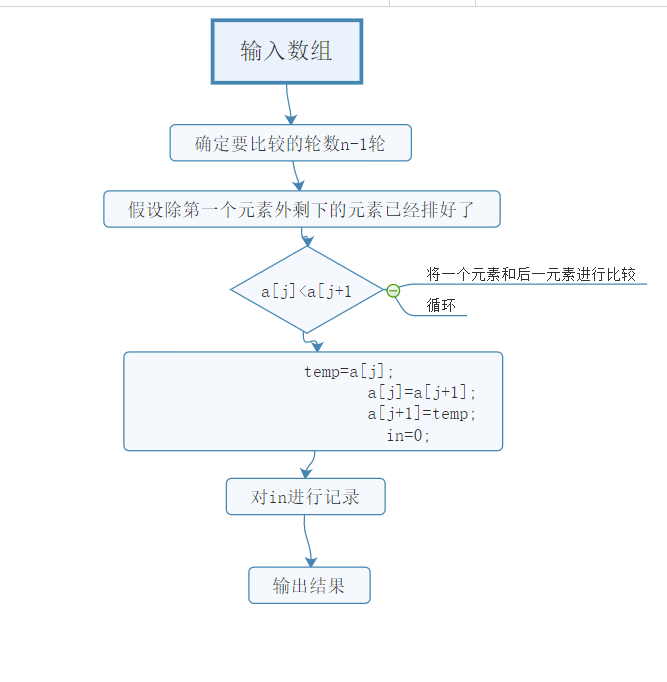
实验所遇问题无。
实验结果截图：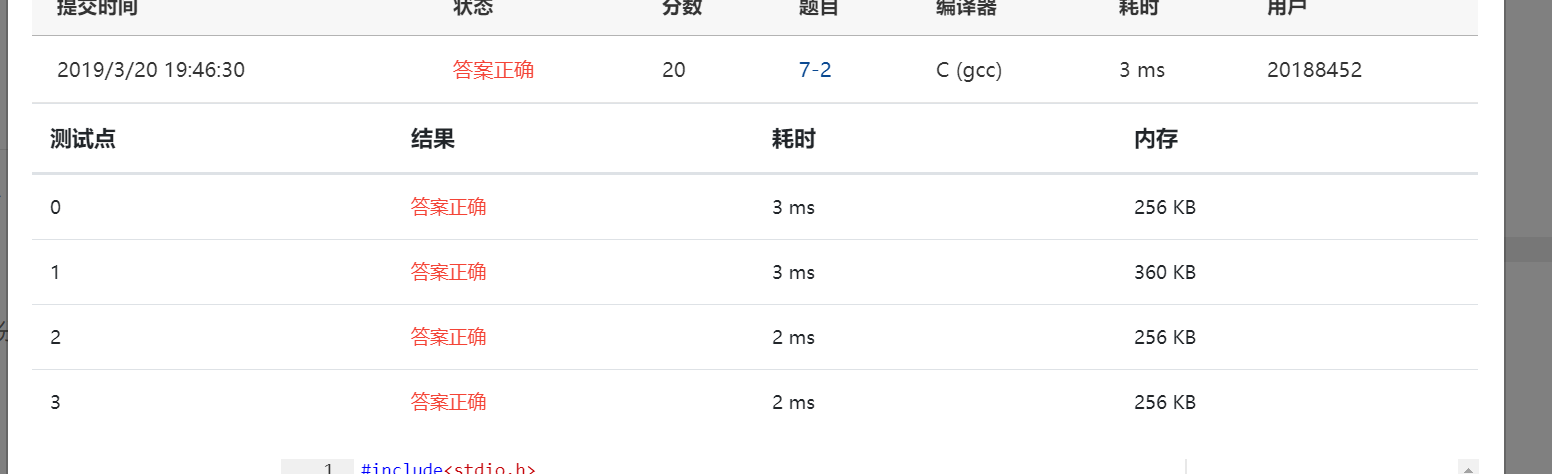
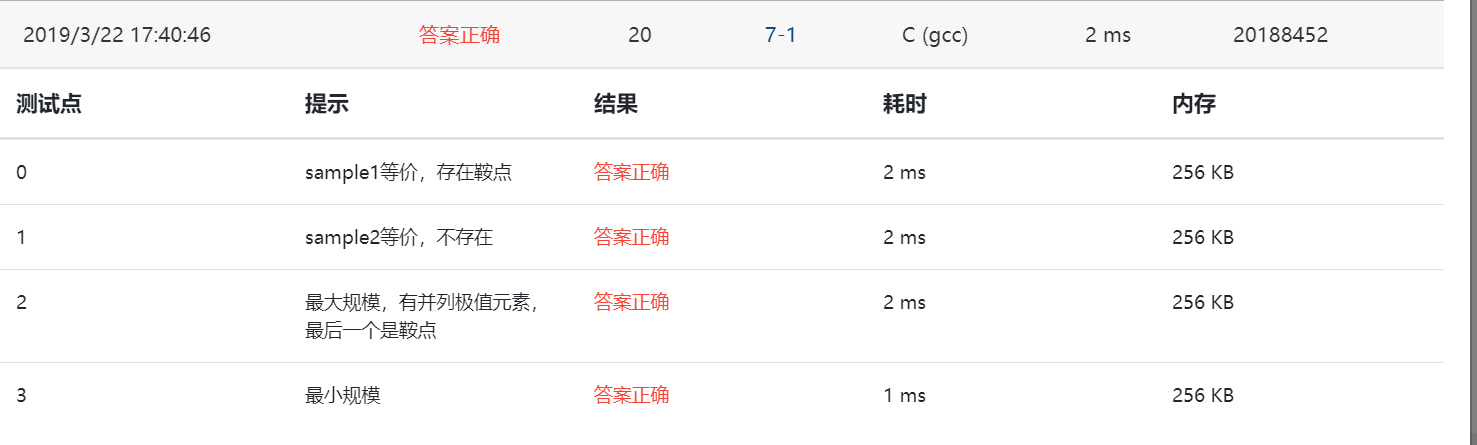
7-1 找鞍点 （20 分)
一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。
本题要求编写程序，求一个给定的n阶方阵的鞍点。
输入格式：
输入第一行给出一个正整数n（1≤n≤6）。随后n行，每行给出n个整数，其间以空格分隔。
输出格式：
输出在一行中按照“行下标 列下标”（下标从0开始）的格式输出鞍点的位置。如果鞍点不存在，则输出“NONE”。题目保证给出的矩阵至多存在一个鞍点。
输入样例1：
4
1 7 4 1
4 8 3 6
1 6 1 2
0 7 8 9
输出样例1：
2 1
输入样例2：
2
1 7
4 1
输出样例2：
NONE
实验代码：
#include <stdio.h>
int main(void)
{
int i,j,k,a[6][6],inmax,max,flag,n;
scanf("%d",&n);
for (i=0;i<n;i++)
for (j=0;j<n;j++)
scanf("%d",&a[i][j]);
for (i=0;i<n;i++){
inmax=a[i][0];
max=0;
for (j=0;j<n;j++)
if (a[i][j]>=inmax){
inmax=a[i][j];
max=j;
}
flag=1;
for (k=0;k<n;k++)
if (inmax>a[k][max]){
flag=0;
continue;
}
if(flag){
printf("%d %d",i,max);
break;
}
}
printf("NONE");
return 0;
}
实验思路：先将数组进行定义，假设a[i][0]最大列号0赋给一个值进行保存，找出第i行的最大数将最大数和最大数的下标分别保存在一个变量中，在将最大数和同列进行比较，如果不是同列最小令flag为0.
思维导图：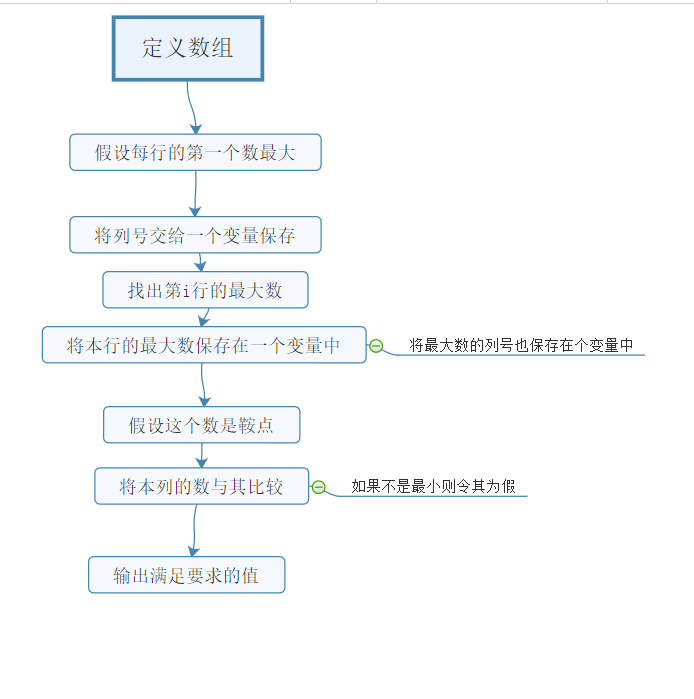
实验所遇问题：开始将数组定义的太小不满足要求。然后将其修改
但发现一直是第三个测试点错误，通过室友解释才明白会存在两个数相等的情况需要将后面的那个数作为鞍点，然后在一个比较中加入一个等于号解决问题。
实验结果截图：
