51Nod1203 2012集训队答辩 JZPLCM

A1339. JZPLCM(顾昱洲)

时间限制：3.0s   内存限制：256.0MB  

试题来源

　　2012中国国家集训队命题答辩

问题描述

　　给定一长度为n的正整数序列a，有q次询问，每次询问一段区间内所有数的lcm(即最小公倍数)。由于答案可能很大，输出答案模1000000007。

输入格式

　　第一行，两个整数，n, q，分别表示数列长度和询问个数。
　　下面n行，每行一个整数，第i行的整数为a_i。
　　下面q行，每行两个整数l, r，表示询问下标i在[l, r]范围内的a_i的lcm。

输出格式

　　q行。对于每个询问，输出一行，表示对应的答案。

样例输入

3 3
123
234
345
1 2
2 3
1 3

样例输出

9594
26910
1103310　　

数据范围

n,q<10w,ai<=1e9。

 

这题这么神我肯定要放上来啊。

首先51Nod的数据是经过弱化的，并没有那么强。

对于51Nod的数据，我们可以用一种比较皮的方法艹过去。

一些数的LCM就是对每个质数的指数取max。
对于大于sqrt(x)的质数，这个指数最大是1。所以对于这些数，我们只需要判断在这些区间内是否出现过就可以了。这个问题可以用莫队算法+桶实现。
对于小于等于sqrt(x)的质数，经过打表发现这种质数只会有约50个。我们可以把每一个数S[i]分解质因数后存进50个表里，每次询问对这50个质数分别来一次区间求最值。因为表定型后不涉及修改操作，可以使用ST表把单次询问降低到O(1)。
所以说这道题需要写两个程序。
莫队算法转移的复杂度是O(1)的，该部分复杂度是O(n*sqrt(n))。
倍增算法预处理的复杂度是O(50*n*log(n))的，处理询问复杂度是O(50*n)的。
鉴于这题空间不是很足，要对每个小质数一个一个处理ST表，空间复杂度为O(n*log(n)+n*50)。

 

但是对于Ai<=1e9就无能为力了。

然后队爷给了一种很强力的做法，发现我的思维能力跟队爷完全不在一个时代上。

一般我做题，先把问题模型化，一般化，再根据数据范围选择合适的算法/数据结构一顿爆艹。

但是队爷做题有两种思路，这就比我不知高到哪里去了。

一种思路：原问题 - 一般化(强化)的问题 - 解决一般化的问题 - 解决原问题。

另一种思路是：先思考某种特殊情况，一般是比较好处理的，再推广到原问题。

其实这种思路在很多解题报告中也有出现：

“我们讨论只有一条链的情况。”

“我们先来看一下没有约束的情况。”

“这个a很讨厌，我们先不管它。”

……

划下重点。

所以我们先来假设每一个数都是无平方因子数。

这种情况我只会莫队，果然是数据结构学傻(不对数据结构也不会写)。

这时候问题化为：某区间所有出现过的数的积(不同数的积)。

这是一个我不会的经典问题，好像之前看到有些题考这个？

 

对于上面的问题，我们考虑对于一组询问[l,r]。

找到每个数上一次出现的位置pre[i](如果没有出现就是0)。

那么就要求的是

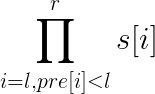
对于这种问题，可以有如下解决方式：

设询问为f(l,r,l)，则询问等价为

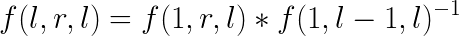
所以你要写一种数据结构，支持上面的操作。

显然可以离线+树状数组。

 

那么有平方甚至多次方因子呢？

假设一个数A[i]可以写成p的q次方(p为质数，q为满足被整除的最大值)。

那可以把这个数拆成q个数p,p^2,p^3……p^q，每个数的权值都是p。

于是问题就转化成了上面的弱化问题，只是区间长度变了而已。

于是这题就解决了(好神啊突然开车)。

 

略显尴尬的是我的代码比较长……

下面放对于51Nod数据的爆艹法。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
#define FILE "JZPLCM"
using namespace std;

const int N = 50010;
const int Mod = 1e9+7;
struct Node{int to,next;}E[N];
int n,m,P[N],vis[N],tot,S[N],Ny[N],block,A[20][N],bel[N],bin[N],B[51][N];
int Log[N],Pw[51][N],Ans[N],res=1,head[N],Tot;
struct Data{
  int l,r,id;
  bool operator <(const Data &d)const{
    if(bel[l]==bel[d.l])return r<d.r;
    return bel[l]<bel[d.l];
  }
}Ask[N];

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline void link(int u,int v){
  E[++tot]=(Node){v,head[u]};
  head[u]=tot;
}

inline void prepare(){
  for(int i=2;i<N;++i){
    if(!vis[i])P[++tot]=i;
    for(int j=1;j<=tot;++j){
      int ytk=i*P[j];if(ytk>=N)break;
      vis[ytk]=1;if(i%P[j]==0)break;
    }
  }
  Ny[1]=1;
  for(int i=2;i<N;++i)
    Ny[i]=1ll*(Mod-Mod/i)*Ny[Mod%i]%Mod;
}

inline void Insert(int x){
  for(int e=head[x];e;e=E[e].next){
    int y=E[e].to;bin[y]++;
    if(bin[y]==1)res=1ll*res*y%Mod;
  }
}

inline void Delete(int x){
  for(int e=head[x];e;e=E[e].next){
    int y=E[e].to;bin[y]--;
    if(bin[y]==0)res=1ll*res*Ny[y]%Mod;
  }
}

inline void Modui(){
  memset(bin,0,sizeof(bin));
  Insert(S[1]);int l=1,r=1;
  for(int i=1;i<=m;++i){
    if(r<Ask[i].r)
      for(int j=r+1;j<=Ask[i].r;++j)
        Insert(S[j]);
    if(r>Ask[i].r)
      for(int j=r;j>Ask[i].r;--j)
        Delete(S[j]);
    if(l<Ask[i].l)
      for(int j=l;j<Ask[i].l;++j)
        Delete(S[j]);
    if(l>Ask[i].l)
      for(int j=l-1;j>=Ask[i].l;--j)
        Insert(S[j]);
    l=Ask[i].l;r=Ask[i].r;
    Ans[Ask[i].id]=1ll*Ans[Ask[i].id]*res%Mod;
  }
}

int main()
{
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);

  prepare();n=gi();m=gi();block=sqrt(n);
  bin[0]=1;for(int i=1;i<=16;++i)bin[i]=bin[i-1]*2;
  for(int i=1,j=0;i<=n;i*=2,j++)Log[i]=j;
  for(int i=1;i<=N;++i)
    if(!Log[i])Log[i]=Log[i-1];
  for(int i=1;i<=n;++i)S[i]=gi(),bel[i]=i/block+1;
  for(int j=1;j<=n;++j){
    int ytk=S[j];
    for(int i=1;i<=50;++i){
      int num=0;
      while(ytk%P[i]==0)num++,ytk/=P[i];
      B[i][j]=num;
      if(ytk==1)break;
    }
    if(ytk>1)link(S[j],ytk);
  }
  for(int i=1;i<=50;++i){
    Pw[i][0]=1;
    for(int j=1;j<=19;++j)
      Pw[i][j]=1ll*Pw[i][j-1]*P[i]%Mod;
  }
  for(int i=1;i<=m;++i){
    int l=gi(),r=gi();Ans[i]=1;
    Ask[i]=(Data){l,r,i};
  }
  for(int k=1;k<=50;++k){
    for(int i=1;i<=n;++i)A[0][i]=B[k][i];
    for(int i=1;i<=16;++i)
      for(int j=1;j<=n;++j)
        A[i][j]=max(A[i-1][j],A[i-1][min(n,j+bin[i-1])]);
    for(int i=1;i<=m;++i){
      int l=Ask[i].l,r=Ask[i].r,dt=r-l+1,Lg=Log[dt];
      int Mx=max(A[Lg][l],A[Lg][r-bin[Lg]+1]);
      Ans[i]=1ll*Ans[i]*Pw[k][Mx]%Mod;
    }
  }
  sort(Ask+1,Ask+m+1);Modui();
  for(int i=1;i<=m;++i)
    printf("%d
",Ans[i]);
  return 0;
}

然后是对于51Nod的数据很多地方跑不过原数据的树状数组。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
#define FILE "JZPLCM"
#define c233 printf("
");
using namespace std;

const int N = 50010;
const int M = N*50;
const int Mod = 1e9+7;

struct Data{
  int r,tr,kind,id;
  bool operator <(const Data &d)const{
    return tr<d.tr;
  }
}opt[N*40];

struct Pair{
  int pre,id,val;
  Pair(){};
  Pair(int p,int i,int v){pre=p;id=i;val=v;}
  bool operator <(const Pair &p)const{
    return pre<p.pre;
  }
}Y[M];

int n,m,P[N],tot,vis[N],A[N],cnt,ED[N],pre[M],bin[N],top,Ans[N],W[M],V[M];
struct BIT{
  int T[M];
  inline void clear(){
    for(int i=0;i<=cnt;++i)T[i]=1;
  }
  inline int lb(int k){
    return k&-k;
  }
  inline void update(int x,int val){
    for(;x<=cnt;x+=lb(x))T[x]=1ll*T[x]*val%Mod;
  }
  inline int query(int x,int res=1){
    for(;x>0;x-=lb(x))res=1ll*res*T[x]%Mod;
    return res;
  }
}T;

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline void prepare(){
  for(int i=2;i<N;++i){
    if(!vis[i])P[++tot]=i;
    for(int j=1,ytk;j<=tot;++j){
      ytk=i*P[j];if(ytk>=N)break;
      vis[ytk]=1;if(i%P[j]==0)break;
    }
  }
}

inline int QPow(int d,int z,int res=1){
  for(;z;z>>=1,d=1ll*d*d%Mod)
    if(z&1)res=1ll*res*d%Mod;
  return res;
}

inline void solve(){
  int i=1,j=1;T.clear();
  while(i<=cnt && j<=top){
    if(Y[i].pre<=opt[j].tr)
      T.update(Y[i].id,Y[i].val),++i;
    else{
      int id=opt[j].id;
      if(opt[j].kind==1)Ans[id]=1ll*Ans[id]*T.query(opt[j].r)%Mod;
      else Ans[id]=1ll*Ans[id]*QPow(T.query(opt[j].r),Mod-2)%Mod;
      ++j;
    }
  }
  while(j<=top){
    int id=opt[j].id;
    if(opt[j].kind==1)Ans[id]=1ll*Ans[id]*T.query(opt[j].r)%Mod;
    else Ans[id]=1ll*Ans[id]*QPow(T.query(opt[j].r),Mod-2)%Mod;
    ++j;
  }
}

int main()
{
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);
  n=gi();m=gi();prepare();
  for(int i=1;i<=n;++i)A[i]=gi();
  for(int i=1;i<=n;++i){
    int ytk=A[i];
    for(int j=1;P[j]<=ytk/P[j];++j)
      if(ytk%P[j]==0){
        W[++cnt]=P[j];ytk/=P[j];V[cnt]=P[j];
        while(ytk%P[j]==0)
          ++cnt,W[cnt]=W[cnt-1]*P[j],V[cnt]=P[j],ytk/=P[j];
      }
    if(ytk>1)W[++cnt]=ytk,V[cnt]=ytk;
    ED[i]=cnt;
  }
  for(int i=1;i<=cnt;++i)pre[i]=bin[W[i]],bin[W[i]]=i;
  for(int i=1;i<=cnt;++i)Y[i]=Pair(pre[i],i,V[i]);
  sort(Y+1,Y+cnt+1);
  for(int i=1;i<=m;++i){
    int l=gi(),r=gi();Ans[i]=1;
    opt[++top]=(Data){ED[r],ED[l-1],1,i};
    opt[++top]=(Data){ED[l-1],ED[l-1],-1,i};
  }
  sort(opt+1,opt+top+1);solve();
  for(int i=1;i<=m;++i)printf("%d
",Ans[i]);
  return 0;
}