BZOJ2301 HAOI2011 Problem b

2301: [HAOI2011]Problem b

Time Limit: 50 Sec  Memory Limit: 256 MB

Description

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

2
2 5 1 5 1
1 5 1 5 2

Sample Output

14
3

HINT

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

　　正解是显而易见的数论。

　　看见这个题目可以马上想到容斥原理：

　　设答案是f(a,b,c,d,k)，那么一定有

　　　　f(a,b,c,d,k)=f(1,b,1,d,k)-f(1,a-1,1,d,k)-f(1,b,1,c-1,k)+f(1,a-1,a,c-1,k)；

　　现在就是要求f(1,n,1,m,k)了。

　　问题转化为求4次“1<=x<=n,1<=y<=m,gcd(x,y)=k的数对数”。

　　这个就是很simple的莫比鸟斯函数题了QwQ。

　　

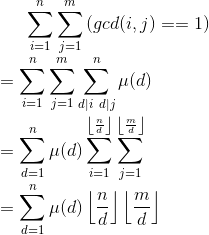
　　然后就是可爱的数论分块，复杂度O(√n)。

　　所以总复杂度就是O(T√n)了。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
using namespace std;

const int N = 50010;
int P[N],tot,miu[N],vis[N],k;
LL Ans;

int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline void prepare(){
  miu[1]=1;
  for(int i=2;i<N;++i){
    if(!vis[i])miu[i]=-1,P[++tot]=i;
    for(int j=1;j<=tot;++j){
      if(i*P[j]>=N)break;
      vis[i*P[j]]=1;
      if(i%P[j])miu[i*P[j]]=-miu[i];
      else{miu[i*P[j]]=0;break;}
    }
  }
  for(int i=2;i<N;++i)
    miu[i]+=miu[i-1];
}

inline int gcd(int a,int b){return b?gcd(b,a%b):a;}

inline int _(int x,int g){
  return x/k+(x%k?1:0)*g;
}

inline LL calc(int n,int m){
  LL ans=0;
  if(n>m)swap(n,m);
  for(int gl=1,gr;gl<=n;gl=++gr){
    gr=min(n/(n/gl),m/(m/gl));
    ans+=1ll*(miu[gr]-miu[gl-1])*1ll*(n/gl)*1ll*(m/gr);
  }
  return ans;
}

int main()
{
  prepare();int Case=gi();
  while(Case--){
    int a=gi(),b=gi(),c=gi(),d=gi();k=gi();
    a=_(a,1);b=_(b,0);c=_(c,1);d=_(d,0);
    //if(b>d)swap(a,c),swap(b,d);
    Ans=calc(b,d)-calc(a-1,d)-calc(b,c-1)+calc(a-1,c-1);
    printf("%lld
",Ans);
  }
  return 0;
}