Digital filter

 https://ww2.mathworks.cn/help/signal/examples/practical-introduction-to-digital-filter-design.html

Design filter via matlab:

d = designfilt(resp,Name,Value) designs a digitalFilter object, d, with response type resp. Specify the filter further using a set of Name,Value pairs. The allowed specification sets depend on the response type, resp, and consist of combinations of the following:

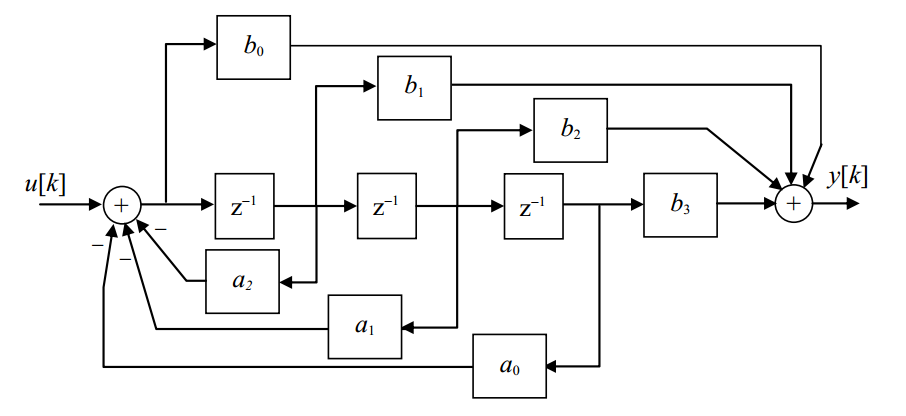
• Frequency constraints correspond to the frequencies at which a filter exhibits a desired behavior. Examples include 'PassbandFrequency'and 'CutoffFrequency'. (See the complete list under Name-Value Pair Arguments.) You must always specify the frequency constraints.

• Magnitude constraints describe the filter behavior at particular frequency ranges. Examples include 'PassbandRipple' and 'StopbandAttenuation'. (See the complete list under Name-Value Pair Arguments.) designfilt provides default values for magnitude constraints left unspecified. In arbitrary-magnitude designs you must always specify the vectors of desired amplitudes.

• 'FilterOrder'. Some design methods let you specify the order. Others produce minimum-order designs. That is, they generate the smallest filters that satisfy the specified constraints.

• 'DesignMethod' is the algorithm used to design the filter. Examples include constrained least squares ('cls') and Kaiser windowing ('kaiserwin'). For some specification sets, there are multiple design methods available to choose from. In other cases, you can use only one method to meet the desired specifications.

• Design options are parameters specific to a given design method. Examples include 'Window' for the 'window' method and optimization 'Weights' for arbitrary-magnitude equiripple designs. (See the complete list under Name-Value Pair Arguments.) designfilt provides default values for design options left unspecified.

• 'SampleRate' is the frequency at which the filter operates. designfilt has a default sample rate of 2 Hz. Using this value is equivalent to working with normalized frequencies.

Note

If you specify an incomplete or inconsistent set of name-value pairs at the command line, designfilt offers to open a Filter Design Assistant. The assistant helps you design the filter and pastes the corrected MATLAB® code on the command line.

If you call designfilt from a script or function with an incorrect set of specifications, designfilt issues an error message with a link to open a Filter Design Assistant. The assistant helps you design the filter, comments out the faulty code in the function or script, and pastes the corrected MATLAB code on the next line.

• Use filter in the form dataOut = filter(d,dataIn) to filter a signal with a digitalFilter, d.

• Use fvtool to visualize a digitalFilter, d.

• Type d.Coefficients to obtain the coefficients of a digitalFilter, d. For IIR filters, the coefficients are expressed as second-order sections.

• See digitalFilter for a list of the filtering and analysis functions available for use with digitalFilter objects.

designfilt(d) lets you edit an existing digital filter, d. It opens a Filter Design Assistant populated with the filter’s specifications, which you can then modify. This is the only way you can edit a digitalFilter object. Its properties are otherwise read-only.

FIR Filter Design

Lowpass Filter Specifications

The ideal lowpass filter is one that leaves unchanged all frequency components of a signal below a designated cutoff frequency, , and rejects all components above . Because the impulse response required to implement the ideal lowpass filter is infinitely long, it is impossible to design an ideal FIR lowpass filter. Finite length approximations to the ideal impulse response lead to the presence of ripples in both the passband () and the stopband () of the filter, as well as to a nonzero transition width between passband and stopband.

Both the passband/stopband ripples and the transition width are undesirable but unavoidable deviations from the response of an ideal lowpass filter when approximated with a finite impulse response. These deviations are depicted in the following figure:

• Practical FIR designs typically consist of filters that have a transition width and maximum passband and stopband ripples that do not exceed allowable values. In addition to those design specifications, one must select the filter order, or, equivalently, the length of the truncated impulse response.

A useful metaphor for the design specifications in filter design is to think of each specification as one of the angles in the triangle shown in the figure below.

The triangle is used to understand the degrees of freedom available when choosing design specifications. Because the sum of the angles is fixed, one can at most select the values of two of the specifications. The third specification will be determined by the particular design algorithm. Moreover, as with the angles in a triangle, if we make one of the specifications larger/smaller, it will impact one or both of the other specifications.

FIR filters are very attractive because they are inherently stable and can be designed to have linear phase. Nonetheless, these filters can have long transient responses and might prove computationally expensive in certain applications.

Minimum-Order FIR Designs

Minimum-order designs are obtained by specifying passband and stopband frequencies as well as a passband ripple and a stopband attenuation. The design algorithm then chooses the minimum filter length that complies with the specifications.

Design a minimum-order lowpass FIR filter with a passband frequency of 0.37*pi rad/sample, a stopband frequency of 0.43*pi rad/sample (hence the transition width equals 0.06*pi rad/sample), a passband ripple of 1 dB and a stopband attenuation of 30 dB.

Fpass = 0.37; 
Fstop = 0.43;
Ap = 1;
Ast = 30;

d = designfilt('lowpassfir','PassbandFrequency',Fpass,...
  'StopbandFrequency',Fstop,'PassbandRipple',Ap,'StopbandAttenuation',Ast);

hfvt = fvtool(d);

The resulting filter order can be queried using the filtord function.

N = filtord(d)

N = 39

You can use the info function to get information about the parameters used to design the filter

info(d)

ans = 17x44 char array
    'FIR Digital Filter (real)                   '
    '-------------------------                   '
    'Filter Length  : 40                         '
    'Stable         : Yes                        '
    'Linear Phase   : Yes (Type 2)               '
    '                                            '
    'Design Method Information                   '
    'Design Algorithm : Equiripple               '
    '                                            '
    'Design Specifications                       '
    'Sample Rate     : N/A (normalized frequency)'
    'Response        : Lowpass                   '
    'Specification   : Fp,Fst,Ap,Ast             '
    'Stopband Atten. : 30 dB                     '
    'Passband Ripple : 1 dB                      '
    'Stopband Edge   : 0.43                      '
    'Passband Edge   : 0.37                      '

Fixed Order, Fixed Transition Width

Fixed-order designs are useful for applications that are sensitive to computational load or impose a limit on the number of filter coefficients. An option is to fix the transition width at the expense of control over the passband ripple/stopband attenuation.

Consider a 30-th order lowpass FIR filter with a passband frequency of 370 Hz, a stopband frequency of 430 Hz, and sample rate of 2 kHz. There are two design methods available for this particular set of specifications: equiripple and least squares. Let us design one filter for each method and compare the results.

N = 30;
Fpass = 370;
Fstop = 430;
Fs = 2000; 

% Design method defaults to 'equiripple' when omitted
deq = designfilt('lowpassfir','FilterOrder',N,'PassbandFrequency',Fpass,...
  'StopbandFrequency',Fstop,'SampleRate',Fs);

dls = designfilt('lowpassfir','FilterOrder',N,'PassbandFrequency',Fpass,...
  'StopbandFrequency',Fstop,'SampleRate',Fs,'DesignMethod','ls');

hfvt = fvtool(deq,dls);
legend(hfvt,'Equiripple design', 'Least-squares design')

Equiripple filters are ideally suited for applications in which a specific tolerance must be met, such as designing a filter with a given minimum stopband attenuation or a given maximum passband ripple. On the other hand, these designs may not be desirable if we want to minimize the energy of the error (between ideal and actual filter) in the passband/stopband.

• If you want to reduce the energy of a signal as much as possible in a certain frequency band, use a least-squares design.

In the examples above, the designed filters had the same ripple in the passband and in the stopband. We can use weights to reduce the ripple in one of the bands while keeping the filter order fixed. For example, if you wish the stopband ripple to be a tenth of that in the passband, you must give the stopband ten times the passband weight. Redesign the equiripple filter using that fact.

deqw = designfilt('lowpassfir','FilterOrder',N,'PassbandFrequency',Fpass,...
  'StopbandFrequency',Fstop,'SampleRate',Fs,...
  'PassbandWeight',1,'StopbandWeight',10);

hfvt = fvtool(deq,deqw);
legend(hfvt,'Equiripple design', 'Equiripple design with weighted stopband')

Fixed Order, Fixed Cutoff Frequency

You can design filters with fixed filter order and cutoff frequency using a window design method.

• You can use different windows to control the stopband attenuation while keeping the filter order unchanged.

For example, consider a 100-th order lowpass FIR filter with a cutoff frequency of 60 Hz and a sample rate of 1 kHz. Compare designs that result from using a Hamming window, and a Chebyshev window with 90 dB of sidelobe attenuation.

dhamming = designfilt('lowpassfir','FilterOrder',100,'CutoffFrequency',60,...
  'SampleRate',1000,'Window','hamming');

dchebwin = designfilt('lowpassfir','FilterOrder',100,'CutoffFrequency',60,...
  'SampleRate',1000,'Window',{'chebwin',90});

hfvt = fvtool(dhamming,dchebwin);
legend(hfvt,'Hamming window', 'Chebyshev window')

There are other ways in which you can specify a filter with fixed order: fixed cutoff frequency, passband ripple, and stopband attenuation; fixed transition width; and fixed half-power (3dB) frequency.

IIR Filter Design

One of the drawbacks of FIR filters is that they require a large filter order to meet some design specifications. If the ripples are kept constant, the filter order grows inversely proportional to the transition width. By using feedback, it is possible to meet a set of design specifications with a far smaller filter order. This is the idea behind IIR filter design. The term "infinite impulse response" (IIR) stems from the fact that, when an impulse is applied to the filter, the output never decays to zero.

• IIR filters are useful when computational resources are at a premium. However, stable, causal IIR filters cannot have perfectly linear phase. Avoid IIR designs in cases where phase linearity is a requirement.

Another important reason for using IIR filters is their small group delay relative to FIR filters, which results in a shorter transient response.

Butterworth Filters

Butterworth filters are maximally flat IIR filters. The flatness in the passband and stopband causes the transition band to be very wide. Large orders are required to obtain filters with narrow transition widths.

Design a minimum-order Butterworth filter with passband frequency 100 Hz, stopband frequency 300 Hz, maximum passband ripple 1 dB, and 60 dB stopband attenuation. The sample rate is 2 kHz.

Fp = 100;
Fst = 300;
Ap = 1;
Ast = 60;
Fs = 2e3;

dbutter = designfilt('lowpassiir','PassbandFrequency',Fp,...
  'StopbandFrequency',Fst,'PassbandRipple',Ap,...
  'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','butter');

Chebyshev Type I Filters

Chebyshev Type I filters attain smaller transition widths than Butterworth filters of the same order by allowing for passband ripple.

• Butterworth and Chebyshev Type I filters both have maximally flat stopbands. For a given filter order, the tradeoff is between passband ripple and transition width.

Design a Chebyshev Type I filter with the same specifications as the Butterworth filter above.

dcheby1 = designfilt('lowpassiir','PassbandFrequency',Fp,...
  'StopbandFrequency',Fst,'PassbandRipple',Ap,...
  'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','cheby1');

Chebyshev Type II Filters

• Chebyshev Type II filters have maximally flat passbands and equiripple stopbands.

Since extremely large attenuations are typically not required, we may be able to attain the required transition width with a relatively small order by allowing for some stopband ripple.

Design a minimum-order Chebyshev Type II filter with the same specifications as in the previous examples.

dcheby2 = designfilt('lowpassiir','PassbandFrequency',Fp,...
  'StopbandFrequency',Fst,'PassbandRipple',Ap,...
  'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','cheby2');

Elliptic Filters

Elliptic filters generalize Chebyshev and Butterworth filters by allowing for ripple in both the passband and the stopband. As ripples are made smaller, elliptic filters can approximate arbitrarily close the magnitude and phase response of either Chebyshev or Butterworth filters.

• Elliptic filters attain a given transition width with the smallest order.

dellip = designfilt('lowpassiir','PassbandFrequency',Fp,...
  'StopbandFrequency',Fst,'PassbandRipple',Ap,...
  'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','ellip');

Compare the response and the order of the four IIR filters.

• For the same specification constraints, the Butterworth method yields the highest order and the elliptic method yields the smallest.

FilterOrders = [filtord(dbutter) filtord(dcheby1) filtord(dcheby2) filtord(dellip)]

FilterOrders = 1×4

     7     5     5     4

hfvt = fvtool(dbutter,dcheby1,dcheby2,dellip);
axis([0 1e3 -80 2]);
legend(hfvt,'Butterworth', 'Chebyshev Type I',...
  'Chebyshev Type II','Elliptic')