遗传算法简介
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。最优化问题的目标函数和约束条件种类繁多,有的是线性的,有的是非线性的;有的是连续的,有的是离散的;有的是单峰值的,有的是多峰值的。随着研究的深入,人们逐渐认识到在很多复杂情况下要想完全精确地求出其最优解既不可能,也不现实,因而求出其近似最优解或满意解是人们的主要着眼点之一。遗传算法为解决这类问题提供了一个有效的途径和通用框架,开创了一种新的全局优化搜索算法。
传统最优算法都是建立在确定性基础上的搜索,在搜索过程中遇到一个决策点时,对于选a还是选b,其结果是确定的。比如贪婪法,就是按照贪婪策略选择,同样的条件下,每个决策选1000次结果都是一样的。随机算法就不会有这么确定的结果,它是一种带启发式的随机搜索,非常适合一些传统方法难以解决的复杂问题或非线性问题,在人工智能、自适应控制、机器学习等领域得到了广泛的应用。
遗传算法原理
遗传算法中将n维决策向量X=[x1 x2 ... xn]T 用n个记号Xi(i=1,2,...,n)所组成的符号串X来表示:X = X1 X2 ... Xn. 把每一个Xi 看做一个遗传基因,它的所有可能取值称为等位基因。这样X就可看做是由n个遗传基因所组成的一个染色体。一般情况下染色体的长度n是固定的,但对一些问题n也可以是变化的。根据不同的情况这里的等位基因可以是一组整数,也可以是某一范围内的实数值,或者是纯粹的一个记号。最简单的等位基因是由0和1这两个整数组成的,相应的染色体就可表示为一个二进制符号串。这种编码所形成的排列形式X是个体的基因型,与它对应的X值是个体的表现型。通常个体的表现型和其基因型是一一对应的,但有时也允许基因型和表现型是多对一的关系。染色体X也称为个体X,对于每一个个体X,要按照一定的规则确定出其适应度。个体的适应度与其对应的个体表现型X的目标函数值相关联,X越接近于目标函数的最优点,其适应度越大;反之其适应度越小。遗传算法中决策变量X组成了问题的解空间。对问题最优解的搜索是通过对染色体X的搜索过程来进行的,从而由所有的染色体X就组成了问题的搜索空间。
生物的进化是以群体为主体的。与此相对应遗传算法的运算对象是由M个个体所组成的集合,称为种群。与生物一代一代的自然进化过程相类似,遗传算法的运算过程也是一个反复迭代过程。第t代群体记做P(t),经过一代遗传和进化后得到第t+1代群体,它们也是由多个个体组成的集合,记做P(t+1)。这个群体不断地经过遗传和进化操作,并且每次都按照优胜劣汰的规则将适应度较高的个体更多地遗传到下一代,这样最终在群体中将会得到一个优良的个体X,它所对应的表现型X将达到或接近于问题的最优解X*
生物的进化过程主要是通过染色体之间的交叉和染色体的变异来完成的。与此相对应,遗传算法中最优解的搜索过程也模仿生物的这个进化过程,使用所谓的遗传算子(genetic operator)作用于群体P(t)中,进行下述遗传操作从而得到新一代群体P(t+1)
1. 选择(selection)
根据各个个体的适应度,按照一定的规则或方法,从第t代群体P(t)中选择出一些优良的个体遗传到下一代群体P(t+1)中。
2. 交叉(crossover)
将群体P(t)内的各个个体随机搭配成对,对每一对个体以某个概率(称为交叉概率,crossover rate)交换它们之间的部分染色体。
3. 变异(mutation)
对群体P(t)中的每一个个体,以某一概率(称为变异概率,mutation rate)改变某一个或某一些基因座上的基因值为其他的等位基因。
遗传算法的运算过程
遗传算法的运算过程如下图所示:
 步骤1:初始化。设置进化代数计数器t=0,设置最大进化代数T;随机生成M个个体作为初始群体P(0);
步骤1:初始化。设置进化代数计数器t=0,设置最大进化代数T;随机生成M个个体作为初始群体P(0);
步骤2:个体评价。计算群体P(t)中各个个体的适应度;
步骤3:选择运算。将选择算子作用于群体;
步骤4:交叉运算。将交叉算子作用于群体;
步骤5:变异运算。将变异算子作用于群体。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1);
步骤6:终止条件判断。若t≤T,则t=t+1,转到步骤2;若t>T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
计算示例
以Ras函数(Rastrigin's Function)为目标函数,求其在x1,x2∈[-5,5]上的最小值。这个函数对模拟退火、进化计算等算法具有很强的欺骗性,因为它有非常多的局部最小值点和局部最大值点,很容易使算法陷入局部最优,而不能得到全局最优解。如下图所示,该函数只在(0,0)处存在全局最小值0。
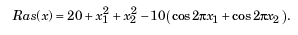


(1)变量编码
遗传算法的运算对象是表示个体的符号串,所以必须把变量x1,x2编码为一种符号串。这里将[-5,5]的区间内的数用10位2进制数表示,将它们连接在一起所组成的20位无符号二进制整数就形成了个体的基因型,表示一个可行解。例如基因型X=00000000001111111111所对应的表现型是X =[-5,5]T。个体的表现型和基因型X之间可通过编码和解码程序相互转换。将10位2进制数码转b换为[-5,5]区间内的实数公式为:f(b) = 10*b/1023 - 5
(2)初始群体的产生
遗传算法是对群体进行的进化操作,需要给其准备一些表示起始搜索点的初始群体数据。种群的个体数决定了遗传算法的多样性。数目越多,种群的多样性越好,但是会增加计算量,降低运行效率。但如果数目过少,会因为遗传多样性降低而导致比较容易出现早熟现象。所谓早熟问题,就是在遗传运算初期,少数个体适应度非常高(可能是局部最优解),这样在遗传过程中,这些个体在下一代所占的比例很高,使得交叉和变异对种群多样性的作用被严重降低,种群多样性无法保证,最终因为局部最优解的存在而错过全局最优解。一般建议种群数目取值最小为20。本例中群体规模的大小取为50,即群体由50个个体组成,每个个体可通过随机方法产生。
(3)适应度计算
遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而确定其遗传机会的大小。本例中,目标函数总取非负值,但是以求函数最小值为优化目标,考虑将1/(Ras(X)+0.01)作为个体的适应度,目标函数Ras(X)的值越大,个体适应度越低。为计算函数的目标值须先对个体基因型X进行解码。由于目标函数可能有正有负,有时求最大值,有时求最小值,因此需要在目标函数与适应度函数之间进行变换。
适应度函数的设计主要应满足以下几个条件:
1.单值、连续、非负。这个条件很容易理解和实现。
2.合理、一致性。要求适应度反映对应解的优劣程度,这个条件的达成往往比较难以衡量
3.计算量小。适应度函数设计应尽可能简单,这样可以减少计算时间,降低计算成本。
4.通用性强。适应度对某类具体问题,应尽可能通用,最好无需使用者改变适应度函数中的参数。
(4)选择运算
选择运算把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。本例中采用与适应度成正比的概率(又称为轮盘赌选择)来确定各个个体复制到下一代群体中的数量。其具体操作过程是首先计算出群体中所有个体的适应度的总和Σfi,其次计算出每个个体的相对适应度的大小fi/Σfi. 每个概率值组成一个区域,全部概率值之和为1。最后再产生一个0到1之间的随机数依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。为了进行说明,假设某种群中有5个个体,每个个体的选择概率(fi/Σfi)分别是:0.1、0.2、0.1、0.4、0.2

假如在区间[0,1]上随机生成一个点0.53,根据累积概率0.4<0.53<0.8,于是第4个个体被选中。由上图可以看出,个体的选择概率(或相对适应度fi/Σfi)越大,被选中的概率就越大。
(5)交叉运算
交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某两个个体之间的部分染色体。本例采用单点交叉的方法,其具体操作过程是:首先对群体进行随机配对,其次随机设置交叉点位置,最后再相互交换配对染色体之间的部分基因。交叉概率决定了新产生个体的频度,这是保证种群多样性的关键参数之一。交叉概率太小,会导致新个体产生速度慢,影响种群多样性,抑制早熟现象的能力就会较差;但是交叉概率不能太大,过高的交叉概率会使基因的遗传变得不稳定,优良的基因比较容易被破坏,使得遗传算法的性能近似于随机搜索算法的性能。一般交叉概率取0.4~0.9之间的值,0.8是比较常用的值。在本例中进行交叉时先生成一个0-1区间内的随机概率p,如果两个待交叉的染色体不同并且 p 小于设定好的交叉概率pc,那么就分别在2进制编码的0:9和10:19位中间随机选取一个位置,交换对应的基因片段,从而形成两个新的个体。假如两条染色体分别如下(染色体中的0:9位代表x2,10:19位代表x1):
1111 0011 1100 0001 1000
0100 0011 0100 1001 1001
在第7位和第16位处交叉(两点交叉),结果为:
1110 0011 1100 1001 1000
0101 0011 0100 0001 1001
(6)变异运算
变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变,它也是产生新个体的一种操作方法。变异概率太小不利于产生新个体,对种群的多样性有影响。但是变异概率太大也会使基因的遗传变的不稳定,优良的基因比较容易被破坏。根据遗传学原理,基因突变是一个小概率事件,在遗传算法中,变异算子对种群的影响也应远远小于交叉算子。一般建议变异概率取值小于0.2。变异算子主要解决两个问题,一是如何确定变异位置,另一个是如何进行基因变异。常用的变异算子有:单点变异--对基因编码随机选择一个点,以随机概率进行变异运算;固定位置变异--对基因上一个或几个固定位置上的基因片段,以随机的概率进行变异;均匀变异--对基因上的每个片段,都使用均匀分布的随机数,以较小的随机概率进行变异运算。具体的变异算法与基因编码方式有关,比如二进制编码和浮点数编码,直接将某一位从1变0,或者从0变1就实现了变异。对符号编码的基因,直接将某个位置上的符号替换成符合该位置要求的其他符号即可实现变异。对于属性序列编码方式,改变某个属性的值也算是实现了变异。总之,变异只是一个抽象的要求,具体的算法实现则千姿百态。
# -*- coding:cp936 -*-
import numpy as np
import matplotlib.pyplot as plt
# 初始化种群
def init():
return np.random.randint(0, 0xFFFFF + 1, size = M)
# 编码转换为决策变量
def B2X(popB,popX):
for i in range(M):
x1 = 10.0 * ((popB[i] & 0xFFC00) >> 10) / 1023.0 - 5.0
x2 = 10.0 * (popB[i] & 0x003FF) / 1023.0 - 5.0
popX[:,i] = np.array([x1, x2])
# 目标函数定义
def ras(x):
y = 20 + x[0]**2 + x[1]**2 - 10*(np.cos(2*np.pi*x[0])+np.cos(2*np.pi*x[1]))
return y
# 适应度计算
def getfitness(popB,popX):
B2X(popB,popX)
fitness = 1.0 / (ras(popX) + 0.01)
return fitness
# 依据适应度选择要进行繁殖的个体
def selection(fitness,popB):
select_probability = fitness/sum(fitness)
cumulative_sum = np.cumsum(select_probability)
indexes = np.searchsorted(cumulative_sum, np.random.random(M))
# resample according to indexes
popB[:] = popB[indexes]
# 进行基因交叉,实现基因交换
def crossover(popB):
np.random.shuffle(popB) # 随机打乱种群中个体的顺序(种群内前一个与后一个配对)
for i in range(M/2):
p = np.random.random() # 随机生成一个0~1内的数
if p < pc: # 如果这个数落在交叉概率区间内,则交换部分基因
index1 = np.random.randint(0,10) # 随机选择交叉点
if (popB[2*i] & (1<<index1)) != (popB[2*i+1] & (1<<index1)):
if (popB[2*i] & (1<<index1)): # 个体1的该位为1(个体2对应位为0)
popB[2*i] &= ~(1<<index1) # 个体1该位变为0
popB[2*i+1]|= (1<<index1) # 个体2该位变为1
else: # 个体1的该位为0(个体2对应位为1)
popB[2*i] |= (1<<index1) # 个体1该位变为1
popB[2*i+1]&= ~(1<<index1) # 个体2该位变为0
index2 = np.random.randint(10,20) # 随机选择交叉点
if (popB[2*i] & (1<<index2)) != (popB[2*i+1] & (1<<index2)):
if (popB[2*i] & (1<<index2)): # 个体1的该位为1(个体2对应位为0)
popB[2*i] &= ~(1<<index2) # 个体1该位变为0
popB[2*i+1] |= (1<<index2) # 个体2该位变为1
else: # 个体1的该位为0(个体2对应位为1)
popB[2*i] |= (1<<index2) # 个体1该位变为1
popB[2*i+1]&= ~(1<<index2) # 个体2该位变为0
# 进行基因变异
def mutation(popB):
for i in range(M):
p = np.random.random() # 随机生成一个0~1内的数
if p < pm: # 如果这个数落在变异概率区间内,则进行变异处理
index = np.random.randint(0,20) # 采用单点变异
if (popB[i] & (1<<index)): # 个体i的该位为1
popB[i] &= ~(1<<index) # 个体i的该位变为0
else:
popB[i] |= (1<<index) # 个体i的该位变为1
if __name__ == '__main__':
M = 50 # 种群大小
T = 100 # 进化代数
pc = 0.8 # 交叉概率
pm = 0.05 # 变异概率
popB = np.zeros(M, dtype='uint32') # 由编码表示的种群
popX = np.zeros((2,M)) # 由决策变量表示的种群
fitness = np.zeros(M) # 个体适应度
fitness_record = np.zeros((2,T)) # 记录适应度随进化代数的变化
popB = init() # 随机初始化种群
t = 0
while t < T:
fitness = getfitness(popB,popX) # 计算适应度
i = np.argmax(fitness)
fitness_record[0,t] = sum(fitness)/M
fitness_record[1,t] = fitness[i]
selection(fitness,popB) # 选择
crossover(popB) # 交叉
mutation(popB) # 变异
t = t + 1
max_index = np.argmax(fitness)
print "X: " , popX[:,max_index]
print "Y: ", ras(popX[:,max_index]) # 计算最小值
plt.plot(np.arange(T),fitness_record[0,:],color='b',label='mean')
plt.plot(np.arange(T),fitness_record[1,:],color='r',label='best')
plt.legend(loc='best')
plt.show()
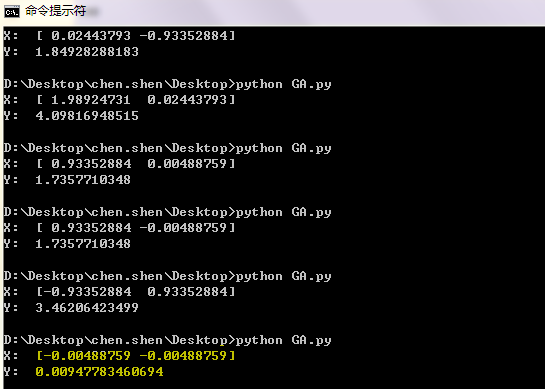
运行几次结果如下图所示,可以发现搜索会经常陷入局部极小值中(早熟),黄色背景的那一次运行找到了全局最小值。对比MATLAB遗传算法工具箱中的结果,发现它也会经常陷入局部极小值。。。至于怎么解决这个问题,这又是另一个问题了。
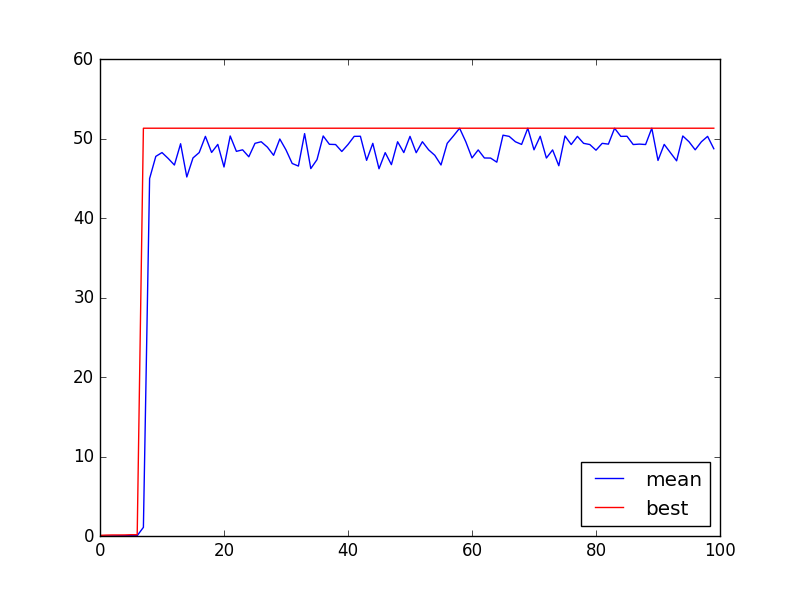
适应度随着进化代数变化曲线如下图所示。其中红色曲线为每一次进化时种群内最大适应度,蓝色曲线为种群的平均适应度。可以发现,随着进化的推进,它们都趋于增大。
遗传算法的特点
为解决各种优化计算问题,人们提出了各种各样的优化算法,如单纯形法、梯度法、动态规划法、分支定界法等。这些优化算法各有各的长处,各有各的适用范围,也各有各的限制。遗传算法是一类可用于复杂系统优化计算的鲁棒搜索算法,与其他一些优化算法相比它主要有下述几个特点:
(1)遗传算法以决策变量的编码作为运算对象。传统的优化算法往往直接利用决策变量的实际值本身来进行优化计算,但遗传算法不是直接以决策变量的值,而是以决策变量的某种形式的编码为运算对象。这种对决策变量的编码处理方式,使得我们在优化计算过程中可以借鉴生物学中染色体和基因等概念,可以模仿自然界中生物的遗传和进化等机理,也使得我们可以方便地应用遗传操作算子。特别是对一些无数值概念,或很难有数值概念而只有代码概念的优化问题,编码处理方式更显示出了其独特的优越性。
(2)遗传算法直接以目标函数值作为搜索信息。传统的优化算法不仅需要利用目标函数值,而且往往需要目标函数的导数值等其他一些辅助信息才能确定搜索方向。而遗传算法仅使用由目标函数值变换来的适应度函数值,就可确定进一步的搜索方向和搜索范围,无须目标函数的导数值等其他一些辅助信息。这个特性对很多无法或很难求导数的目标函数,或导数不存在的函数的优化问题,以及组合优化问题等,应用遗传算法就显得比较方便,因为它避开了函数求导这个障碍。再者,直接利用目标函数值或个体适应度,也使得我们可以把搜索范围集中到适应度较高的部分搜索空间中,从而提高了搜索效率。
(3)遗传算法同时使用多个搜索点的搜索信息。传统的优化算法往往是从解空间中的一个初始点开始最优解的迭代搜索过程。单个搜索点所提供的搜索信息毕竟不多,所以搜索效率不高,有时甚至使搜索过程陷于局部最优解而停滞不前。遗传算法从由很多个体所组成的一个初始群体开始最优解的搜索过程,而不是从一个单一的个体开始搜索。对这个群体所进行的选择、交叉、变异等运算,产生出的乃是新一代的群体,在这之中包括了很多群体信息。这些信息可以避免搜索一些不必搜索的点,所以实际上相当于搜索了更多的点,这是遗传算法所特有的一种隐含并行性。
(4)遗传算法使用概率搜索技术。很多传统的优化算法往往使用的是确定性的搜索方法,一个搜索点到另一个搜索点的转移有确定的转移方法和转移关系,这种确定性往往也有可能使得搜索永远达不到最优点,因而也限制了算法的应用范围。而遗传算法属于一种自适应概率搜索技术,其选择、交叉、变异等运算都是以一种概率的方式来进行的,从而增加了其搜索过程的灵活性。虽然这种概率特性也会使群体中产生一些适应度不高的个体,但随着进化过程的进行,新的群体中总会更多地产生出许多优良的个体。实践和理论都已证明,在一定条件下遗传算法总是以概率1收敛于问题的最优解。当然,交叉概率和变异概率等参数也会影响算法的搜索效果和搜索效率,所以如何选择遗传算法的参数在其应用中是一个比较重要的问题。而另一方面,与其他一些算法相比,遗传算法的鲁棒性又会使得参数对其搜索效果的影响尽可能低。
谢谢XX已失联
参考:https://www.cnblogs.com/21207-iHome/p/6013894.html
###
动态规划算法入门,这就够了
动态规划(Dynamic programming,简称DP),是大家都觉得比较难以掌握的算法。为了应付面试,我们经常会背诵一下斐波那楔数列或者背包问题的源码,其实,只要理解了思想,掌握基本的模型,然后再来点写代码的套路,动态规划并没有那么难。

思想与性质
首先,动态规划最重要的是掌握他的思想,动态规划的核心思想是把原问题分解成子问题进行求解,也就是分治的思想。
那么什么问题适合用动态规划呢?我们通过一个现实中的例子,来理解这个问题。大家可能在公司里面都有一定的组织架构,可能有高级经理、经理、总监、组长然后才是小开发,今天我们通过这个例子,来讲讲什么问题适合使用动态规划。又到了一年一度的考核季,公司要挑选出三个最优秀的员工。一般高级经理会跟手下的经理说,你去把你们那边最优秀的3个人报给我,经理又跟总监说你把你们那边最优秀的人报给我,经理又跟组长说,你把你们组最优秀的三个人报给我,这个其实就动态规划的思想!

首先是重叠子问题,不同的问题,可能都要求1个相同问题的解。假如A经理想知道他下面最优秀的人是谁,他必须知道X,Y,Z,O,P组最优秀的人是谁, 甲总监想知道自己下面最优秀的人是谁,也要去知道X,Y,Z组里面最优秀的人是谁?这就有问题重叠了,两个人都需要了解X,Y,Z三个小组最优秀的人。
其次是最优子结构,最优解肯定是有最优的子解转移推导而来,子解必定也是子问题的最优解。甲总监下面最优秀的3个人肯定是从X,Y,Z提交上来的3份名单中选择最优秀的三个人。例如Q哥是X组长下面的第5名,那么他肯定不可能是甲总监下面最优秀的三个。
第三是无后效性,这个问题可能比较难理解,也就是求出来的子问题并不会因为后面求出来的改变。我们可以理解为,X组长挑选出三个人,即便到了高级经理选出大部门最优秀的三个人,对于X组来说,最优秀的还是这3个人,不会发生改变。
过程
动态规划问题,大致可以通过以下四部进行解决。
1.划分状态,即划分子问题,例如上面的例子,我们可以认为每个组下面、每个部门、每个中心下面最优秀的3个人,都是全公司最优秀的3个人的子问题
2.状态表示,即如何让计算机理解子问题。上述例子,我们可以实用f[i][3]表示第i个人,他手下最优秀的3个人是谁。
3.状态转移,即父问题是如何由子问题推导出来的。上述例子,每个人大Leader下面最优秀的人等于他下面的小Leader中最优秀的人中最优秀的几个。
4.确定边界,确定初始状态是什么?最小的子问题?最终状态又是什么。例如上述问题,最小的子问题就是每个小组长下面最优秀的人,最终状态是整个企业,初始状态为每个领导下面都没有最优名单,但是小组长下面拥有每个人的评分。
经典模型
1.线性模型
最经典的问题就是斐波那楔数列的问题,每个数的值都是一个状态,可以用F[i]表示表示第i个数的值是多少。每个数都是由F[i-1]+F[i-2]转移而来。
另外一个经典的问题就是最长上升自序列(LIS),有一串序列,要求找出它的一串子序列,这串子序列可以不连续,但必须满足它是严格的单调递増的且为最长的。把这个长度输出。示例:1 7 3 5 9 4 8 结果为4。
我们非常容易表示他的状态,我们用f[i]表示以第i个数结尾的,最大的上升自序列是多少?那么它是怎么转移的呢?非常容易想到肯定是从左边的的数转移而来,能转移的数满足什么条件呢?肯定是比a[i]更小的。
线性模式还可以拓展成二维问题,例如背包问题,用f[i][j]表示前i个物品,凑成大小为j的背包,最大的价值是多少。
这类问题非常的多,但是思路都是这样,无非就是从左往右,从上到下,从低维到高维进行转移。
2.区间模型
对于每个问题,都是由子区间推导过来的,我们称之为区间模型,下面是一个例子。
我们有一个连续的序列,每个序列上面都是一个数字c[i],每次我们都能够消灭一个连续的回文子序列,消灭之后左右会合并,成为一个新序列,问最少需要多少次才能够把整个序列消灭掉。回文就是从左到有从右到左读到的序列都是一样的。题目比较抽象,我们通过一些例子来说明这个问题吧?例如一开始的序列是1 4 4 2 3 2 1,那么我们最少需要2次,先消灭掉4 4 , 然后再消灭调1 2 3 2 1.第二个例子是 1 2 3 4 5 5 3 1,我们先消灭掉2 然后再消灭掉4, 最后消灭 1 3 5 5 3 1, 需要3次。
我们经常用f[i][j]来表示消灭i,j区间需要的代价,文末有链接详细叙述这个问题,大家感兴趣的可以看一看。
3.树状模型
我们在数据结构树上面进行最求最优解、最大值等问题,上述我们讲的这个绩效考核就是一个树状模型,具体不再累叙。
实现的套路
我们实现动态规划算法,常用的是2个实现套路,一个是自底向上,另外一个是自顶向下。无论是何种方式,我们都要明确动态规划的过程,把状态表示、状态转移、边界都考虑好。
1.自底向上,简单来说就是根据初始状态,逐步推导到最终状态,而这个转移的过程,必定是一个拓扑序。如何理解这个拓扑序问题呢,甲总监下面有X,Y,Z两个小组,甲总监不会一拿到X组最优秀的三个人,就立马去跟A经理汇报,而是要等到Y,Z小组也选出来之后,也就是自己下面所有子问题都解决了,才会继续向汇报。如果推导的过程不是一个拓扑序,那么要么得到错误的结果,要么算法就要退化。
自底向上一般用来解决什么问题呢?那就是可以轻松确定拓扑序的问题,例如线性模型,都是从左往右进行转移,区间模型,一般都是从小区间推导到大区间。自底向上的一个经典实现是斐波那楔数列的递推实现,即F[i] = F[i - 1] + F[i - 2] 。
2.自顶向下,也就是从最终状态出发,如果遇到一个子问题还未求解,那么就先求解子问题。如果子问题已经求解,那么直接使用子问题的解,所以自顶向下动态规划又有一个形象生动的名字,叫做记忆化搜索,一般我们采用递归的方式进行求解。

自顶向下,我们一般用在树上面,因为我们根据父亲结点,很容易找到所有的子问题,也就是所有的子结点,而自底向上的话,我们要去统计这个结点的所有兄弟结点是否已经实现。会稍微复杂一点,而且比较难理解。
无论是自顶向下还是自底向上,都只是代码实现的一种套路,随便你采用哪一个,都是可以解的,只是看你的选择而已。
动态规划,更多的还是要多练习,题目很多,但万变不离其宗,还是要多多练习。后面还会分享出更多动态规划面试算法真题,大家有兴趣的话可以关注。谢谢大家。
感谢沙茶敏碎碎念,
尽管看到的不是懂
https://baijiahao.baidu.com/s?id=1631319141857419948&wfr=spider&for=pc

