插入排序和分治排序

What’s more important than performance?

> modularity

> correctness

> maintainability

> functionality

> robustness

> user-friendliness

> programmer time

> simplicity

> extensibility

> reliability

Why study algorithms and performance?

> Algorithms help us to understand scalability.

> Performance often draws the line between what is feasible and what is impossible.

> Algorithmic mathematics provides a language for talking about program behavior.

> The lessons of program performance generalize to other computing resources. 

> Speed is fun!

插入排序法（少量数据排序较好，是一种增量排序方法）：O(n2)

说明：缩进代表程序结构，三角形代表注释，箭头表示赋值。

Running time

• The running time depends on the input: an already sorted sequence is easier to sort.

• Parameterize the running time by the size of the input, since short sequences are easier to sort than long ones.

• Generally, we seek upper bounds on the running time, because everybody likes a Guarantee.

Kinds of analyses

Worst-case: (usually)

• T(n) = maximum time of algorithm on any input of size n.

Average-case: (sometimes)

• T(n) = expected time of algorithm over all inputs of size n.

• Need assumption of statistical distribution of inputs.

Best-case: (bogus)

• Cheat with a slow algorithm that works fast on some input

 

分治排序：O(nlogn)（是一种分结合并算法或递归算法）

算法：

时间复杂度：

可以证明，其复杂度为O(nlogn)。

下面看一个例子：

有这样一组数据，{5,4,1,22,12,32,45,21}，如果对它进行合并排序的话，首先将它从中间分开，这样，它就被分成了两个数组{5,4,1,22} {12,32,45,21}.

对这两个数组，也分别进行这样的操作，逐步的划分，直到不能再划分为止(每个子数组只剩下一个元素)，这样，划分的过程就结束了。

划分的过程如下图所示：

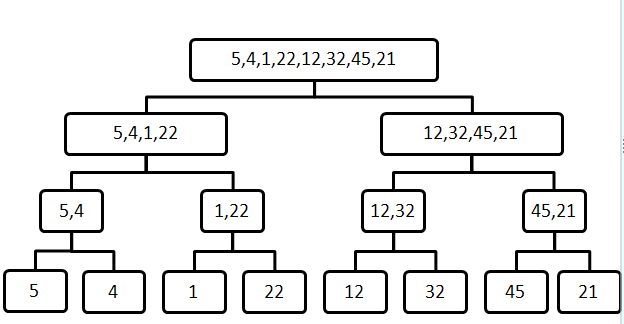
　　接下来，我们进行合并操作，依照上图，划分过程是从上到下进行的，而合并的过程是从下往上进行的，例如上图中,最下层{5},{4}这两个数组，如果按升序排列，将他们合并后的数组就是{4,5}。{1}，{22}这两个子数组合并后是{1,22}。而{4,5}与{1,22}，这两个数组同属一个分支，他们也需要进行合并，由于这两个子数组本身就是有序的，所以合并的过程就是，每次从待合并的两个子数组中选取一个最小的元素，然后把这个元素放到合并后的数组中，前面两个数组合并后就是{1,4,5,22}。依次类推，直到合并到最上层结束，这是数据的排序已经完成了。

合并的过程如下图所示。这个过程是从下往上的。

C语言实现代码如下：

 1#include <stdlib.h>
 2
 3//合并过程
 4void merge(int data[],int start,int mid,int end){
 5
 6
 7 int *tmpLeft,*tmpRight;
 8 int leftSize,rightSize;
 9 int l,r,j;
10
11    printArray(data,8);
12    printf("\n");
13    l = 0;
14    r = 0;
15    j = 0;
16    leftSize = mid - start + 1;
17    rightSize = end - mid;
18
19    tmpLeft = (int *)malloc(leftSize * sizeof(int));
20    tmpRight = (int *)malloc(rightSize * sizeof(int));
21
22 while(j < leftSize){
23        tmpLeft[j] = data[start + j];
24        j++;
25    }
26
27    j = 0;
28
29 while(j < rightSize){
30        tmpRight[j] = data[mid + 1 + j];
31        j++;
32    }
33
34    j = 0;
35
36 while(l < leftSize && r < rightSize){
37 if(tmpLeft[l] < tmpRight[r]){
38
39            data[start + j++] = tmpLeft[l++];
40
41        }else{
42
43            data[start + j++] = tmpRight[r++];
44        }
45    }
46
47 while(l < leftSize){
48        data[start + j++] = tmpLeft[l++];
49    }
50
51 while(r < rightSize){
52        data[start + j++] = tmpRight[r++];
53    }
54
55    free(tmpLeft);
56    free(tmpRight);
57}
58
59
60void merge_sort(int data[],int start,int end){
61
62 int mid;
63 if(start < end){
64 //将数组划分
65        mid = (start + end) / 2;
66        merge_sort(data,start,mid);
67        merge_sort(data,mid + 1,end);
68 //合并划分后的两个数组
69        merge(data,start,mid,end);
70    }
71
72}