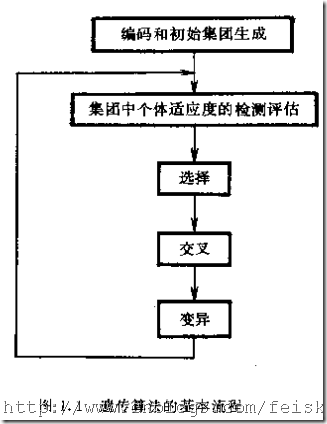
遗传算法(Genetic Algorithm, GA)是模拟达尔文的遗传选择和自然淘汰的生物进化工程的计算模型,它由美国Michigan大学J.Holland教授于1975年首先提出。
GA是全局寻优的优化算法,简单通用,鲁棒性强,适用于并行处理,应用范围广。
从上述的流程可以看出,遗传算法包括5个基本要素:参数编码,初始群体设定,适应度函数的设计,遗传操作,控制参数的设定(群体大小、遗传操作的概率等)。
遗传算法的优点:
(1)处理的对象的不是参数本身,而是对参数及进行了编码的个体。
(2)同时对多个个体进行评估,具有较好的全局搜索性能,减少陷入局部最优解的风险。
(3)仅用适应度函数值来评估个体,适应度函数不受连续可微的约束,其定义域可以任意指定,这样就大大扩展了其应用范围。
(4)采用概率变迁规则来指导它的搜索方向。
遗传算法的主要应用领域
遗传算法今后的主要课题
- 优化搜索方向的研究;
- 学习系统的遗传算法研究;
- 生物进化与遗传算法的研究;
- 遗传算法的秉性分布处理;
- 人工生命与遗传算法的研究。
一个小例子:
题目:求解下列函数的最大值
max f(x)=xsin(10*pi*x)+2,x∈[-1,2]
1: 2: %fminbnd 单变量,黄金分割法,插值法 3: x1=1.5; 4: x2=2;5: [x,fval]=fminbnd('-x*sin(10*pi*x)-2',x1,x2) %max
6: 7: %fminunc 单多变量,梯度最优化算法 8: x1=1.5; 9: x2=2;10: [x,fval]=fminunc('-x*sin(10*pi*x)-2',x1,x2) %max
11: 12: %fminsearch 多变量 Nelder算法 13: x1=1.5; 14: x2=2;15: [x,fval]=fminsearch('-x*sin(10*pi*x)-2',x1,x2) %max
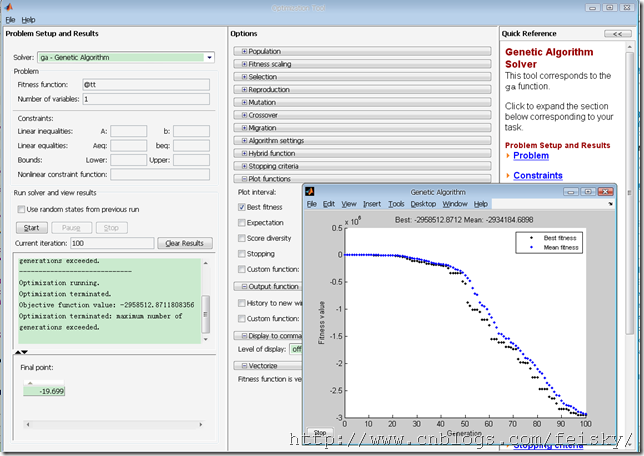
采用遗传算法:(Matlab R2008a)
function y=cc(x) y=-x*sin(10*pi*x)-2; clc;clear all; close all; FitnessFunction=@cc; numberOfVariables=1; LB=1.5; UB=2; [x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],LB,UB)
GA GUI工具:optimtool(‘ga’) gatool
参考书籍:《MATLAB遗传算法工具箱及应用 》《遗传算法及其应用》